初探地球潮汐对静力水准系统的影响

何晓业 许少峰 汪 鹏

(中国科学技术大学 合肥 230029)

静力水准系统(HLS)具有精度高、可进行实时监测等优点[1]，其应用领域广泛。国际加速器准直测量装置中均安装了HLS系统，位于瑞士日内瓦的欧洲核子研究中心(CERN)将要建造的大型自由电子激光装置，将在地下数十米的隧道里建造数公里的直线加速器(CLIC)，对高程监测的精度提高至200 m距离达到2 μm的精度要求，可见高精度的静力水准系统对于加速器准直工作至关重要。我国的正负电子对撞机 BEPCⅡ以及上海光源工程都应用HLS作为重要部件的水准实时监测[2,3]。此外，在大型桥梁、高层建筑、水电站、高铁铁轨的垂直位移等变形监测方面均发挥着重要的作用。

HLS的测量精度会受到地球潮汐(包括海洋潮和固体潮)、温度和压力、系统周围的超大物体如高山、高层建筑等产生的重力异常的影响。这些影响因素在精密工程测量中均须加以修正，本文重点探讨地球潮汐对HLS的精度影响。

1 实验方案

1.1 地球潮汐

根据地球潮汐理论可知，作用在地球上任一点的潮汐力(称为引潮力)定义为日月和其他天体对该点的引力与地心的引力之差。地球潮汐是地球在引潮力作用下的受迫运动，可根据现代天文学精确地预测引潮天体的运行轨道，给出精密轨道参数，利用万有引力定律便可获得地球表面和内部任意一点受到的天体引潮力。

由天体引潮位理论[4]，月球对地球引潮位为：

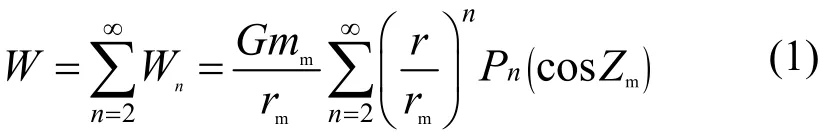
其中mm为月球质量，G为万有引力常数，rm为月-地球心距离，Zm为月亮的地心天顶距，r为地球上一点到地心距离，P式为勒让德(Legendre)多项式。

按照引潮位的杜德森(Doodson)[5]展开，把天顶距按照天体地心天顶距公式展开为赤纬和地方时角的函数，得到多种球谐潮波，如1/3日潮、半日潮汐、周日潮汐、长周期潮汐等不同变化周期的潮汐。本文通过静力水准系统传感器的实验数据初探这些不同变化周期的潮汐。

1.2 方案分析

通过HLS获得地球表面的真正形变量数据，即将HLS读数中包含的地球形变量抽取出来，即： 地球形变=HLS初始读数-潮汐影响量-扰动影响量。

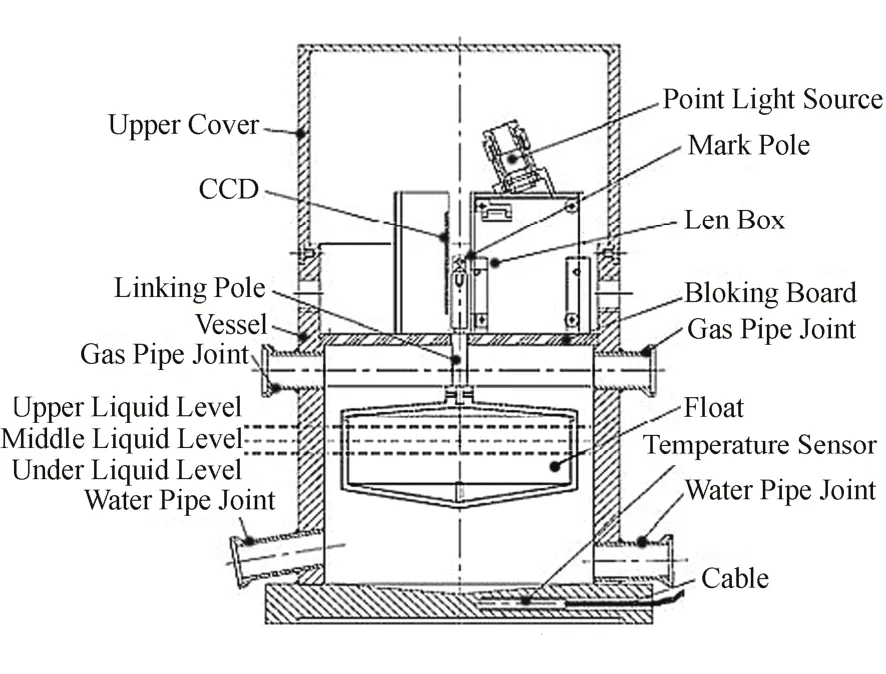
图1 传感器结构图Fig.1 Structure of the sensor.

加速器准直工作要实现μm级精度的地球形变改正量，是复杂而艰巨的任务。因为得到HLS读数后，可看出较明显的液面变化，导致液面变化不仅由于天体引潮力对系统中液面的影响、固体地球潮的影响，且包括HLS中各个钵体温度不均匀、外界噪声等影响。此外，我们目前使用的接触式传感器，是基于CCD的数字式静力水准传感器(图1)，各个钵体传感器在工作中通过连接水管注入一定量的工作液体，浮子随着液位面的高低而上下移动，通过连接杆带动标志物也作上下移动[6]。鉴于传感器结构，浮子本身的小范围摆动会给传感器的测量精度带来影响，以致对HLS读数产生影响，须予以剔除。

研究地球潮汐的实验装置分布于南北方向，总长20 m，布局如图2所示。

图2 实验装置布局和照片Fig.2 The equipment layout and photo.

2 实验数据分析

我们从2011年7月14日开始采集数据，间隔1 h采数一次，持续至9月23日，各传感器数据经温度补偿后的变化如图3所示。

图3 第一和第五传感器的数据(采样间隔1 h)Fig.3 Data from Sensors 1 and 5, in sampling interval of 1 h.

图3显示，第一个和最后一个传感器的数据变化趋势基本相反，直观反映了潮汐现象的存在。为客观反映潮汐现象，须用傅里叶变换法分解信号，使其成为频率的函数，将信号在时间域中的波形转变为频率域的频谱，获得信号的频谱分布。因此，可对任何一个传感器数据进行频谱分析，本文选择第一个传感器的数据。其频谱图见图 4，但其数据并未明显反映潮汐现象，其原因可能为：(1)系统安装初期，人员走动较多，系统可能不稳定；(2) 采集数据的间隔时间较长，不能明显反映出潮汐现象；(3) 周围环境的噪声很多，尤其是低频噪声，需对信号进行滤波处理去除噪声。

为进一步分析，9月23号后，每隔20 min采集一次数据，且人员仅在需采数时去实验区，把人为干扰降至最低。首尾两传感器数据经温度补偿后的结果见图 5。对第一个传感器的数据作平滑和滤波处理得到的频谱见图 6，可清晰看到，在频率约为1.2×10–5、2.4×10–5和3.6×10–5Hz处出现2个峰值，经计算，正好是周期约为11.6、23.1和7.7 h，基本吻合了主要潮汐的周期特征，即半日潮汐、周日潮汐、1/3日潮，说明实验方案是合理的，验证了地球潮汐对HLS的影响。

图4 第一传感器数据的频谱图(采样间隔1 h)Fig.4 Frequency spectra of Sensor 1, in sampling interval of 1 h.

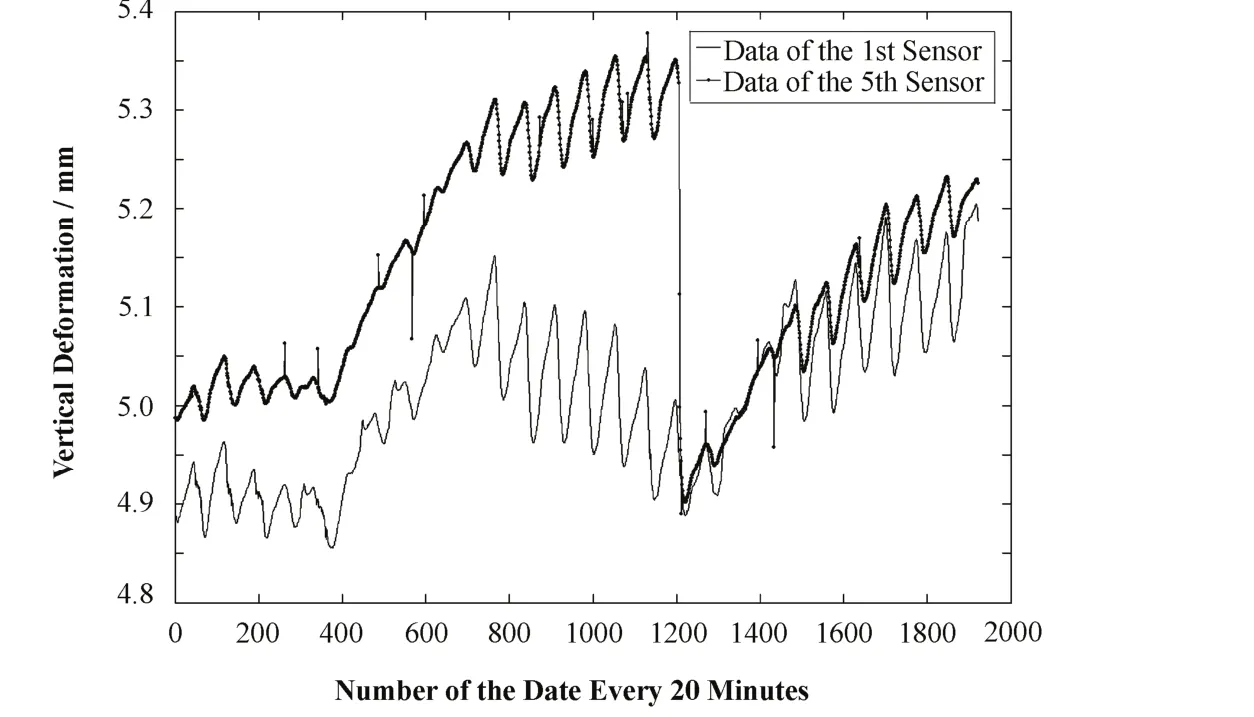
图5 第一和第五传感器的数据(采样间隔20 min)Fig.5 Data from Sensors 1 and 5, in sampling interval of 20 min.

图6 第一个传感器数据的频谱分析图(采样间隔20 min)Fig.6 Frequency spectra of Sensor 1, in sampling interval of 20 min.

3 结语

本文介绍了当前用于粒子加速器准直测量以及监测地球潮的静力水准系统及其应用，分析了影响HLS读数的因素，对静力水准系统得出的数据进行了频谱分析。结果表明，潮汐周期约为 11.6、23.1和7.7 h，基本吻合主要潮汐的周期特征，即半日潮汐、周日潮汐、1/3日潮，说明实验方案是合理的，验证了地球潮汐对HLS的影响。

1 何晓业. 静力水准系统在大科学工程中的应用及发展趋势[J]. 核科学与工程, 2006, 26(4): 332–333

HE Xiaoye. Application of hydrostatic leveling system in key scientific engineering and its developing tendency[J]. Nucl Sci Eng, 2006, 26(4): 332–333

2 何晓业, 黄开席, 陈森玉, 等. 一种用于高能加速器高程监测的静力水准系统[J]. 核技术, 2007, 30(6): 486–487

HE Xiaoye, HUANG Kaixi, CHEN Senyu, et al, A hydrostatic leveling system for position monitoring of high energy accelerator[J]. Nucl Tech, 2007, 30(6): 486–487

3 何晓业, 吴 军. 上海光源静力水准系统的安装与调试[J]. 核技术, 2010, 33(5): 326–329

HE Xiaoye, WU Jun. Installation and debugging of the hydrostatic leveling system at SSRF[J]. Nucl Tech, 2010, 33(5): 326–329

4 Kudrvavtsev S M. Improved harmonic development of the earth tide-generating potential[J]. J Geodesy, 2004, 77(12): 829–838

5 Doodson A T. The harmonic development of the tide generating potential[J]. Proc Royal Soc London, Series A, 1921, 100(704): 305–329

6 何晓业. 静力水准系统的最新发展及应用[M]. 合肥:中国科学技术大学出版社, 2010

HE Xiaoye. The latest developments and applications of HLS[M]. Hefei: Univ Sci Technol China Press, 2010