半规则三角网格模型细分曲面重构
2012-03-19陈甜甜
陈甜甜 赵 罡
(北京航空航天大学 机械工程及自动化学院,北京 100191)
根据已有产品实物样件的坐标测量数据,重新建立样件的数字化模型,再利用计算机辅助技术进行分析、设计、数控加工编程,制造出所需的新产品就是逆向工程[1].三维模型重构技术是逆向工程的一个关键技术.
随着近十几年来细分理论基础的逐步加深与拓展[2-4],细分造型技术已经成为三维模型造型技术中非常重要的一类技术.与工业造型的标准工具NURBS方法相比,细分造型技术具有以下优势:①能够在任意复杂拓扑的网格上不断运用细分规则生成光滑的细分曲面,克服了NURBS须经曲面裁剪和曲面拼接来表达复杂曲面的不足;②细分曲面采用离散数据表示,从而在显示和数控加工中不需将曲面离散化,减少了中间转换过程;③细分是基于递归细化控制网格的技术,其本身具有天然的多分辨率性质,易于构造细分小波.细分小波是多分辨思想与细分曲面结合的最佳体现.
鉴于上述细分造型技术的诸多优点,细分曲面重构就成为众多学者研究的热点.在1994年,文献[5]就提出基于Loop细分的曲面重构方法,该方法拟合精度高但是引入非线性优化代价大.文献[6]研究了双循环过程来拟合控制网格,但未考虑初始网格模型的细节特征.文献[7]提出了保持尖锐特征的Loop细分曲面拟合.在此基础上,文献[8]改进了网格形状优化以及求重采样网格的方法,但该方法需解庞大的线性方程组,还需讨论解的奇异性.
最近,文献[9]提出的渐进插值逼近方法成为曲面重构的新热点.该方法通过不断迭代修改初始网格控制顶点,得到插值于初始控制网格的非均匀B样条曲面.文献[10]将该方法推广到细分曲面,提出了渐进插值(PI,Progressive Interpolation)方法.文献[11]提出与渐进插值思想类似的几何算法,但是未能证明收敛性.文献[12]将该算法推广到拟合算法.此外,文献[13]对曲面局部拟合进行了研究,文献[14]对基于最小二乘优化曲面拟合问题进行了探讨.
上述重构方法不管是拟合还是插值,所生成的细分曲面都无法利用细分曲面的多分辨特性,无法直接进行细分小波分析.这是因为,半规则网格,即具有细分连接性的网格是细分小波应用的重要前提.所以,如何将测量后的非规则密集三角网格模型重构为半规则细分曲面,以此作为最终建立的CAD模型可以直接进行细分小波分析就是本文研究的主要内容.
本算法首先用简化方法将初始网格模型M简化得到基网格M0,其次用插值Loop细分对基网格进行1~2次细分得到网格M1,然后对M1重采样得到网格M2,最后用PI方法得到插值于M2的控制网格M3,其极限曲面就是半规则三角网格的细分曲面.
1 基网格的生成
基网格是通过对初始网格进行简化得到的.文献[15]提出了一种多分辨参数化方法MAPS(Multiresolution Adaptive Parameterization of Surface),可以建立多分辨率网格,从而直接进行细分小波分析.但是该方法由于对每个删除点需要逐层投影,并且对每个新生成的顶点需要逐个定位,计算繁琐费时.为了提高运算效率下面给出一种不需计算删除点逐层投影的简化算法来得到基网格.这里采用提取尖锐特征点和最大独立点集删除的方法来得到高保真度的基网格.
提取尖锐特征点首先判断一条边是否为特征边.这可以通过它的2个共享三角形的外法向夹角确定[8].判断一个点是否为特征点,由该点所连接临边的的特征边的个数所确定.若一个顶点的临边没有特征边,则该点为光滑点.
1.1 网格简化
正文网格简化过程中首先需要确定当前所要删除的所有顶点,每次简化所删除的顶点集合应满足最大独立点集[15]的要求.对于给定网格,最大独立点集不唯一.图1中黑色的圆点构成一组最大独立点集.
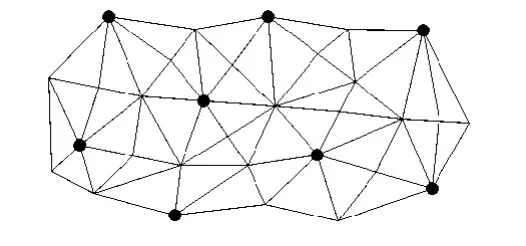
图1 最大独立点集为黑色标记的圆点
最大独立点集的选取要保证删除当前最大独立点集对网格曲面整体影响最小,即删除一组最大独立点集后,要最大化的保存初始网格特征.为了量化顶点的删除优先级,采用面积评价函数a(i)和曲率评价函数k(i)来确定每个顶点的删除优先权值 ω(i)[15]:

式中N(i)表示顶点 pi周围1-邻域点集合.在CAD/CAM中,离散曲率是至关重要的几何不变量,其计算公式采用由Meyer等人提出的离散高斯曲率的离散形式[16]来计算:
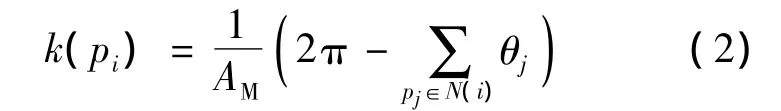
式中,θj表示边 pipi-1与 pipi+1的夹角;AM表示顶点pi周围1-邻域所有锐角三角形和钝角三角形的混合面积.
计算出所有网格上的顶点的优先权值ω(i)后,即可选择当前网格的最大独立点集进行删除,每删除一个顶点将留下一个空洞,需要对此空洞重新进行三角剖分.按照上述删除最大独立点集的方法不断删除顶点,直到无法继续删除为止.至此,设初始网格为Mj,获得简化的基网格具体步骤如下:
1)保留网格Mj中所有度大于12的顶点,以及标记为尖锐特征的顶点;
2)对网格Mj中剩余顶点按评价函数计算权值ω(i),按照由小到大的顺序进行排序并建立顶点队列Qj;
3)依次判断Qj中顶点pi是否应被删除,得到删除顶点的最大独立点集Dj,将Dj中的顶点依次删除;
4)将删除顶点pi及其1-邻域顶点进行保角映射,记录平面坐标,删除顶点pi,并将其构成的多边形进行Delaunay三角剖分;
5)记录剖分后顶点pi周围1-邻域点的拓扑信息,修改pi周围邻域点的拓扑信息.
由于MAPS算法在每次简化时,需遍历初始网格的所有顶点,计算复杂度为O(N log N).本文的简化算法在生成基网格时只需逐层删除最大独立点集,直接利用被删除点周围1-邻域Delaunay三角剖分后的拓扑关系构造简化网格,计算复杂度为O(log N),提高了计算效率.
2 复杂网格重构
2.1 插值Loop细分模式
在将初始网格M简化成基网格M0后,对基网格M0进行1~2次Loop细分得到半规则网格M1.在删除最大点集时仅改变了pi周围1-邻域点的拓扑信息,顶点pi的位置并未改变.这个过程希望尽可能多的保留初始网格上的顶点,进而作为初始网格的采样点以提高精度,故采用插值Loop 细分模式进行细分[17].
具体地,边点的调整分为内部边点pe和边界边点p'e2种情况,其中内部边点pe周围的4个顶点分别是临点p0和p1及对顶点p2和p3;边界边点p'e周围的2个顶点是p0和p1.插值Loop细分边点细分模版分别见式(3)和式(4).
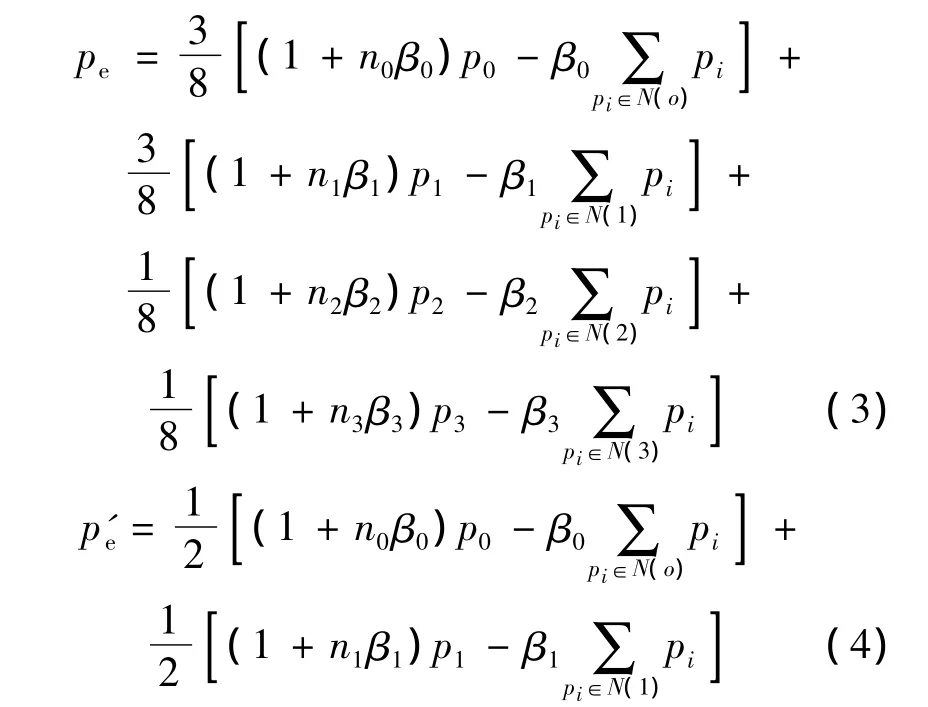
式中
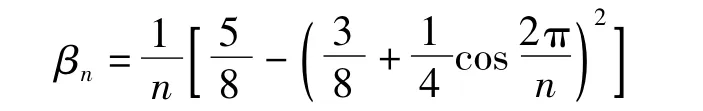
Loop细分后的半规则网格M1与初始网格M的偏离程度还是很大的.按照MAPS方法接下来需要寻找每个顶点以及删除点对应的三角形,如何定位三角形是一个比较棘手的问题.所以下面利用最近点调整网格,得到重采样网格M2.
2.2 最近点调整
最近点调整的主要思路是首先计算简化网格M0上的顶点pi的极限位置p∞i,通过调整顶点pi的位置,使其成为初始网格M0上的采样点.其中调整顶点pi位置的关键问题就是寻找顶点pi在初始网格M0上的最近点,即寻找顶点pi的极限点到初始网格M的投影点μi.
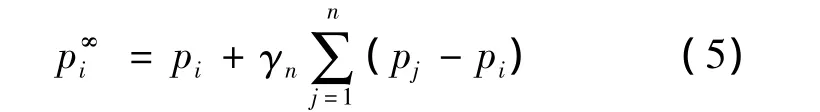
式中
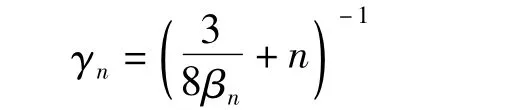
计算最近点μi时首先计算与初始网格M中所有点的有向距离,一般认为在顶点pi外侧的有向距离为正向.最短的有向距离有可能不唯一,则根据求得的法失方向分别与该顶点周围1-邻域三角面片求交点,距离最近的点为μi;若没有交点,令与1-邻域三角面最近距离点为的法失方向由pi的1-邻域三角形的法失方向按照三角形面积加权确定.由于在插值Loop细分时仅插入边点,顶点位置未改变,故只需求边点在初始网格上的最近点.调整网格顶点会使网格中的部分三角形质量有所下降,可以通过Laplacian算子对网格进行平滑处理[8].
2.3 PI方法
至此,得到初始网格的采样网格M2,将M2作为给定的网格,根据式(5)计算其极限曲面对于网格M2中的每一个顶点V0,计算其与对应极限位置的距离,等距更新每一个网格顶点V1=V0+D0,此时得到迭代一次后的新网格.接下来同样地,计算的极限曲面,等距更新中所有顶点 V2=V1+D1,其中.按照上面的迭代过程,得到一系列Loop细分曲面不断逼近采样网格M2,重构的Loop细分曲面S就是逼近初始网格M0的半规则细分曲面.这里采用双向 Hausdroff距离计算误差[18],见式(6).
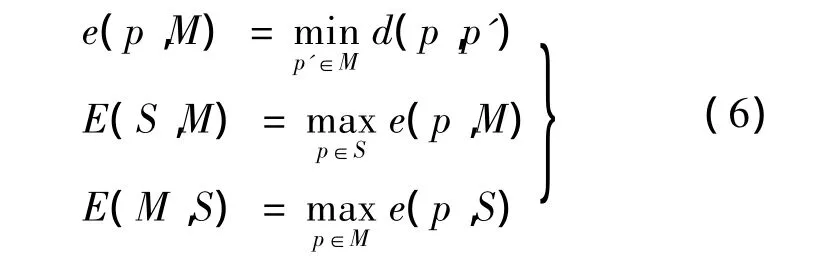
3 实验结果与讨论
为验证上述算法的有效性,结合OpenGL在Visual C++6.0下实现该算法.实验环境是基于Windows XP操作系统,奔腾IV 3.0GHz处理器,1GB内存.采用的数据结构是半边数据结构.
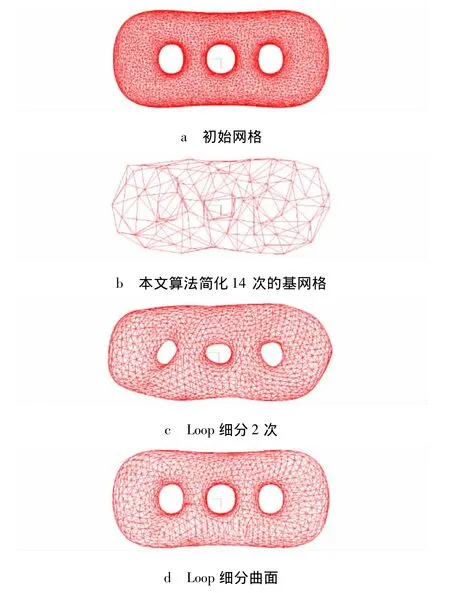
图2 3孔环模型进行细分曲面重构
首先以文献[15]中3孔环模型为例(图2).对具有12000个三角片和5996个顶点的初始网格进行简化14次,快速得到了具有196个三角片和94个顶点的基网格.与初始网格相比,Loop细分2次后得到半规则网格(图2c)有明显的变形.调整后迭代插值初始网格得到图2d,可以看出无尖锐特征的3孔模型重构后的曲面质量良好.
图3为分别对cow模型和tiger模型进行细分曲面重构.图3a和图3d是2个模型的渲染图.首先将2个模型分别简化5次,得到基网格(图3b和图3e).然后,按照第2节的方法进行重采样,通过调整半规则网格边点的位置不断迭代插值得到重构的细分曲面,如图3c和图3f.在牛角、牛尾、虎耳和虎尾等处,重构后的细分曲面很好的保持了初始网格的尖锐特征.
图4a是casting模型的初始网格实体图,共有5096个顶点.提取尖锐特征后,简化14次得到具有1790个顶点的基网格实体图(图4b).经插值Loop细分1次后按照第2节最近点调整采样点,迭代插值得到半规则细分曲面的实体图,如图4c所示.
本文重构的细分曲面实例具体数据见表1.可以看出,部分模型重构后的网格顶点个数稍多于初始网格顶点数,主要原因在于本文以顶点增多为代价使得细分曲面保持尖锐特征的同时具有细分连接性.这对于下一步进行细分小波分解而言是可以接受的.
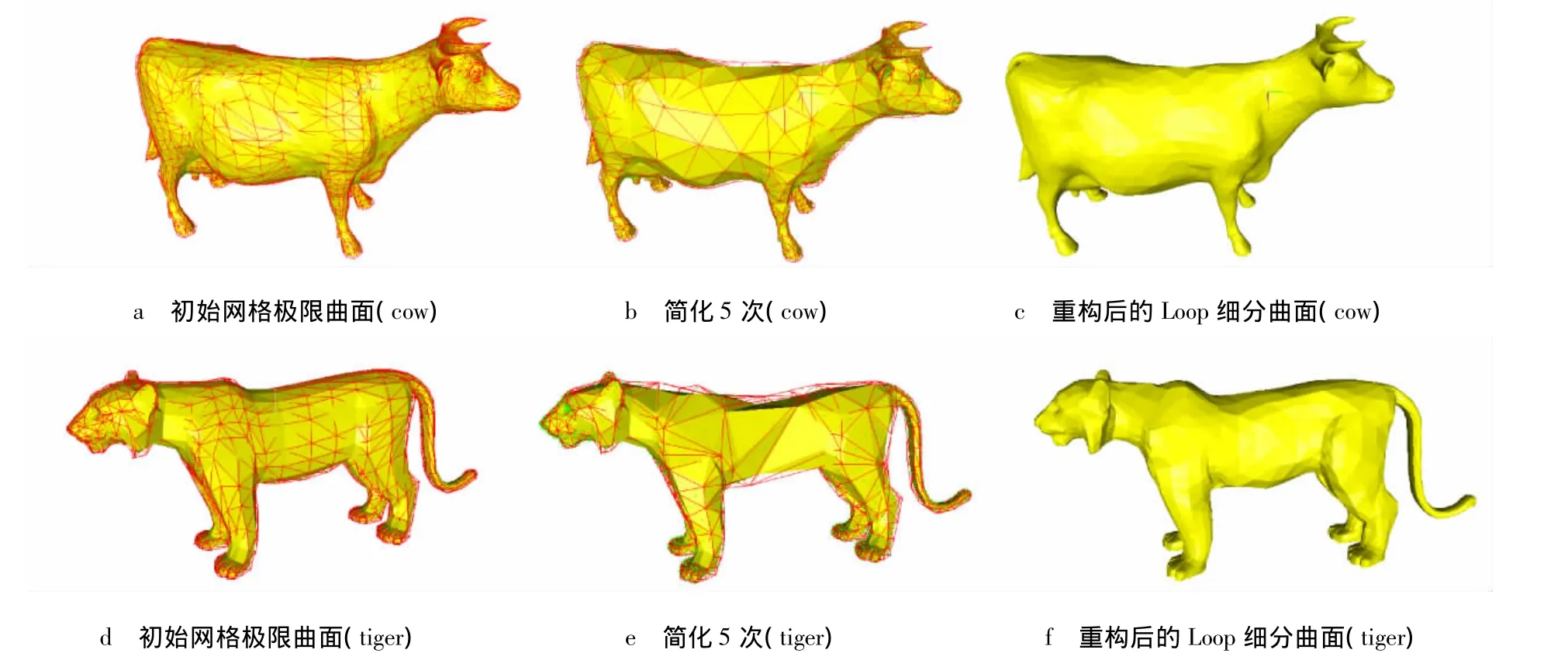
图3 cow模型和tiger模型细分曲面重构

图4 casting模型细分曲面重构
文献[12]中的方法拟合精度高,但是为了调整网格正则度,采用1-4分裂插入顶点法,只能从一定程度上缓解网格的不规则性,大部分网格的连接性还是不够好,不能直接进行细分小波分析.
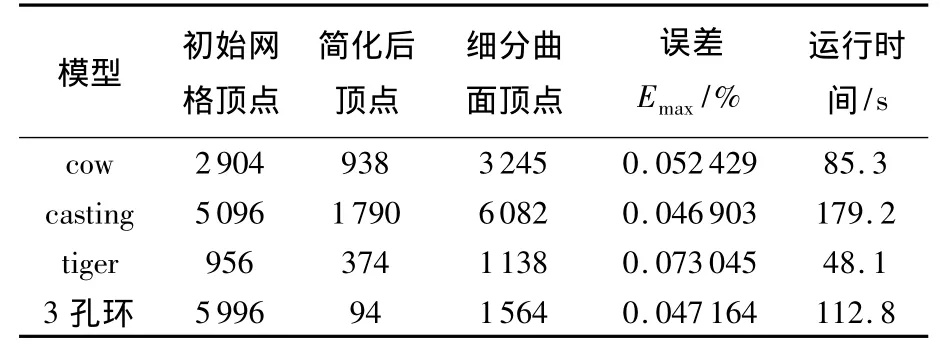
表1 本文算法细分曲面重构实例
4 结论
利用细分小波技术可以得到逼近于初始模型的不同分辨率下的几何模型.本文以得到半规则三角网格模型作为出发点,研究了逆向工程中的三角网格重构问题.在删除最大独立点集的同时,通过提取三角剖分后删除点周围1-邻域点的拓扑关系快速得到基网格,对重采样的基网格通过PI方法不断迭代得到插值半规则网格的Loop细分曲面.与传统网格重构方法相比,本文提出的算法无需解线性方程组,所重构出的细分曲面不仅能保持初始网格的尖锐特征,而且重构后的三角网格细分曲面可以直接进行细分小波变换,是进一步利用细分造型技术进行多分辨分析及编辑的基础.未来的工作包括优化算法以提高大规模网格重构曲面的质量,同时提高算法效率以便更加利于工程应用.
References)
[1]黄诚驹,李鄂琴,禹诚.逆向工程项目式实训教程[M].北京:电子工业出版社,2004:1-17 Huang Chengju,Li Eqin,Yu Cheng.Reversing engineering project type training tutorial[M].Beijing:Publishing House of Electronics Industry,2004:1 -17(in Chinese)
[2] Jiang Qingtang,Li Baobin,Zhu Weiwei.Interpolatory quad/triangle subdivision schemes for surface design[J].Computer Aided Geometric Design,2009,24(8):904 -922
[3] Sadeghi J,Samavati F F.Smooth reverse Loop and Catmull-Calrk subdivision[J].Graphical Models,2011,73(5):200 -117
[4] Olsen L,Samamati F F,Bartels R H.Multiresolution for curves and surfaces based on constraining wavelets[J].Computer Graphics,2007,31(3):449 - 462
[5] Hoppe H,DeRose T,Duchamp T,et al.Piecewise smooth surface construction[C]//Proceedings of the21st Annual Conference on Computer Graphics and Interactive Techniques.New York:ACM Press,1994:295 -302
[6] Suzuki H,Takeuchi S,Kimura F,et al.Subdivision surface fitting to a range of points[C]//The Seventh Pacific Conference on Computer Graphics and Applications.Washington DC:IEEE Computer Society Press,1999:158 - 167
[7] MaWeiyin,Ma Xiaohu,Tso Shiu-Kit,et al.A direct approach for subdivision surface fitting from a dense triangle mesh[J].Computer-Aided Design,2004,36(6):525 -536
[8]李桂清,马维银,鲍虎军.带尖锐特征的Loop细分曲面拟合系统[J].计算机辅助设计与图形学学报,2005,17(6):1179-1185 Li Guiqing,Ma Weiyin,Bao Hujun.Fitting system using loop subdivision surfaces with sharp features[J].Journal of Computer-Aided Design & Computer Graphics,2005,17(6):1179 -1185(in Chinese)
[9] Lin H,Wang G,Dong C.Constructing iterative non-uniform B-spline curve and surface to fit data points[J].Science in China,2003,33:912 -923
[10] Cheng Fuhua,Fan Fengtao,Lai Shuhua,et al.Loop subdivision surface based progressive interpolation[J].Journal of Computer Science and Technology,2009,24(1):39 -46
[11] Maekawa T,Matsumoto Y,Namiki K.Interpolation by geometric algorithm[J].Computer-Aided Design,2007,39(4):313 -323
[12] Yu N,Masayuki M,Takashi M.Loop subdivision surface fitting by geometric algorithms[C]//Poster Proceedings of Pacific Graphics.Tokyo:Computer Graphics Forum,2008:67 -74
[13] Wang Jun,Yu Zeyun.Quality mesh smoothing via local surface fitting and optimum projection[J].Graphical Models,2011,73(4):127–139
[14] Simon F,Michael H.Surface fitting and registration of point clouds using approximations of the unsigned distance function[J].Computer Aided Geometric Design,2010,27(1):60 - 77
[15] Lee AW F,Sweldens W,Schroder P,et al.MAPS:multiresolution adaptive parameterization of surfaces[C]//Proceedings of the 25th annual Conference on Computer Graphics and Interactive Techniques.New York:ACM Press,1998:95 -104
[16] Meyer M,Desbrun M,Schroder P,et al.Discrete differential-geometry operators for triangulated 2-manifolds[C]//International Workshop on Visualization and Mathematics.Berlin:Springer-Visualization and Mathematics,2002:52 -58
[17]白杰.基于小波的细分曲面数控加工技术研究[D].北京:北京航空航天大学机械工程及自动化学院,2009 Bai Jie.Research on NC machining based on the subdivision technology and subdivision wavelets[D].Beijing:School of Mechanical Engineering and Automation,Beijing University of Aeronautics and Astronautics,2009(in Chinese)
[18] Cignoni P,Rocchini C,Scopigno CR.Metro:measuring error on simplified surfaces[J].Computer Graphics Forum,1998,17(2):167-174
