基于优化理论的GPS定位解算算法

赵 鑫 秦红磊 郎荣玲

(北京航空航天大学 电子信息工程学院，北京 100191)

GPS(Global Positioning System)定位解算是根据伪距、伪距率等测量值，计算接收机的位置P、速度V和时间T等信息的过程.在现有的接收机中一般采用最小二乘方法和EKF(Extended Kalman Filter)作为定位解算的方法.最小二乘方法简单易于实现且计算速度快，但是定位精度低且鲁棒性差.EKF算法是近似的非线性滤波方法，其精度高于最小二乘法，但EKF只是对非线性的系统及观测模型进行局部的线性化，并未完全解决系统的非线性滤波问题［1－5］.

针对以上传统定位解算方法存在的问题，本文提出了一种新的定位解算算法——基于优化理论的最大后验估计算法.可以在拥有较高精度的同时采用一种非线性的估计方法进行定位解算.该方法用优化理论的思路求解系统状态量的最大后验概率估计值.它是从系统状态量、观测量的联合概率密度函数出发，将估计问题转化成优化问题，用优化问题的解法对系统的状态进行估计.

本文的主要内容是:首先介绍GPS接收机中定位解算的基本原理;在此基础上，介绍了GPS接收机基于优化理论的最大后验估计定位解算算法的推导过程，以及推导出的优化问题的求解方法.最后，本文采用基于模拟器产生的数据进行了实验验证，有效证明了新提出的GPS定位解算方法能完全解决定位解算中的非线性问题，并拥有较高的定位精度.

1 GPS接收机定位解算原理

空中某点的位置可以通过测量它到空中一些已知位置的距离来获得.在空间三维情况下，由于测量得到的接收机到卫星之间的距离中存在着未知的固定偏差，所以定位解算至少需要4颗卫星和4个距离才能确定用户的位置.式(1)、式(2)即为由伪距、伪距率确定用户位置的基本方程［6－7］.

通过GPS接收机对m(m≥4)颗卫星信号传输时间的测量可得到用户与m颗相应卫星的伪距，列方程得

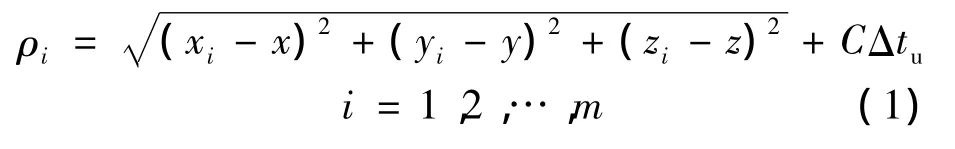
通过GPS接收机对m(m≥4)颗卫星信号多普勒频移的测量可得到用户与m颗相应卫星的伪距率，对式(1)求时间的导数，可得伪距变化率方程:

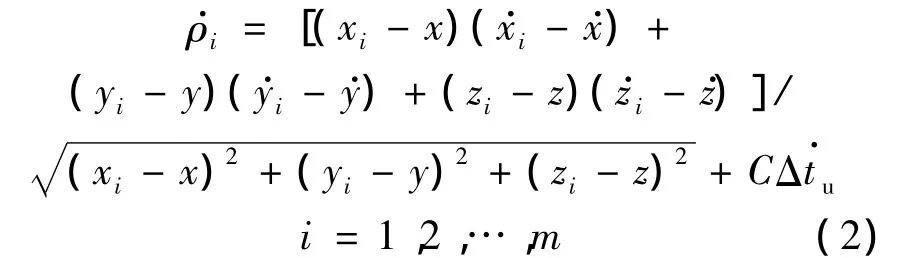
式中，ρi为第 i颗卫星测得的伪距离;(xi，yi，zi)为已知卫星位置;Δtu为待求用户钟差;为第i颗卫星测得的伪距离变化率;)为已知卫星速度;(x，y，z)为待求用户位置，由位置解算得到为待求的用户三维速度;为待求用户钟差变化率.

在下面推导的定位解算新方法中，将式(1)、式(2)作为定位解算系统建模中的量测方程.

2 基于优化理论的定位解算算法

定位解算过程的数学模型属于量测模型非线性，观测噪声和驱动噪声是高斯白噪声的非线性高斯系统.

下面将具体讲述定位解算新方法——基于优化理论的最大后验概率估计方法的推导.

2.1 状态模型

GPS导航系统状态模型可取为

其中

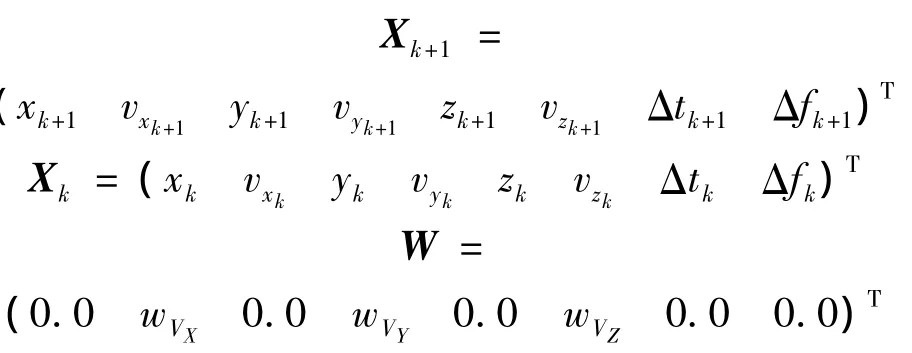
观测矩阵F可取为

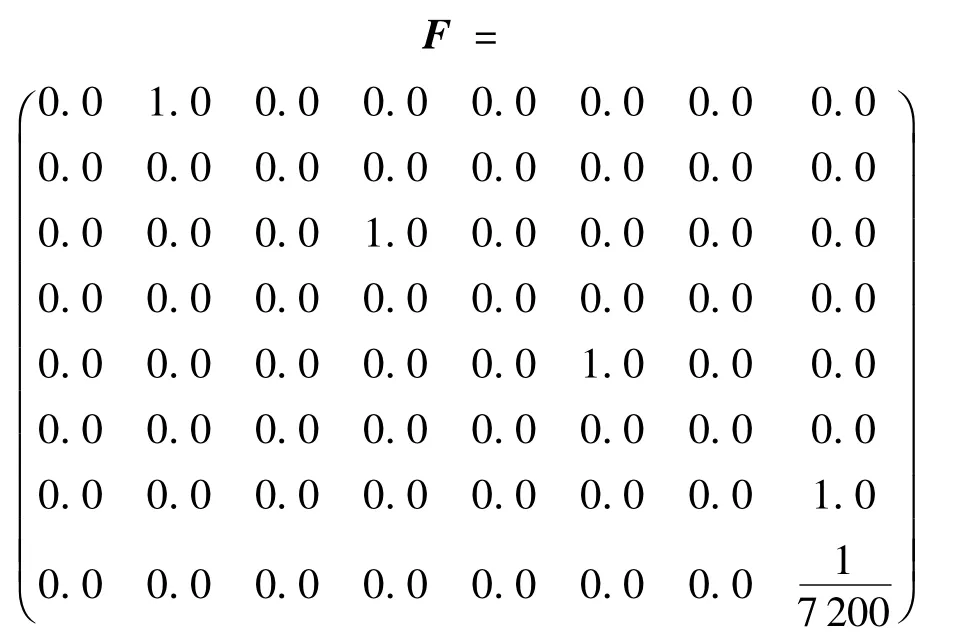
式中，(x，y，z)为用户在大地坐标系中的三维坐标;(vx，vy，vz)为用户在大地坐标系中的三维速度;Δt，Δf为用户接收机的时差与频差;wVX，wVY，wVZ为高斯白噪声.

2.2 算法的数学推导

在给定的系统状态方程、量测方程模型下，用优化算法对给定的系统状态量确定一种估计，这种估计使系统状态量的后验概率最大［8－9］.

假设定位解算系统的模型可以简写为

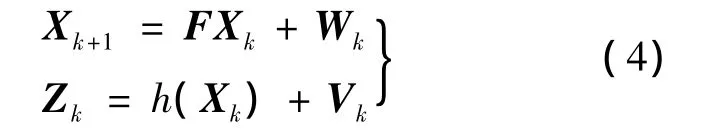
这里，h 关于 X 连续可微，Xk∈Rm，Wk∈Rm，Zk∈Rr并且 Vk∈Rr，r为可见卫星颗数的两倍，m为状态量的个数，这里取8.在模型中序列{Wk}，{Vk}，X0的分布满足以下概率密度函数:

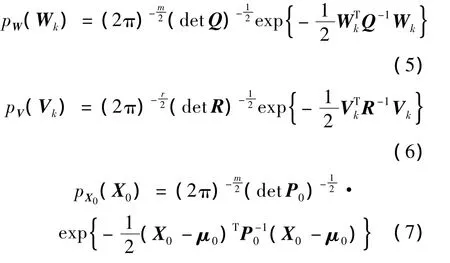
利用概率密度函数变换规则，由模型式(4)可以得到条件概率密度函数:

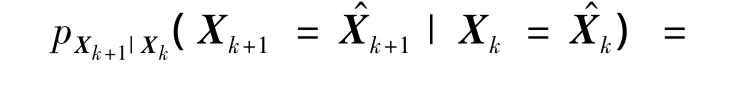
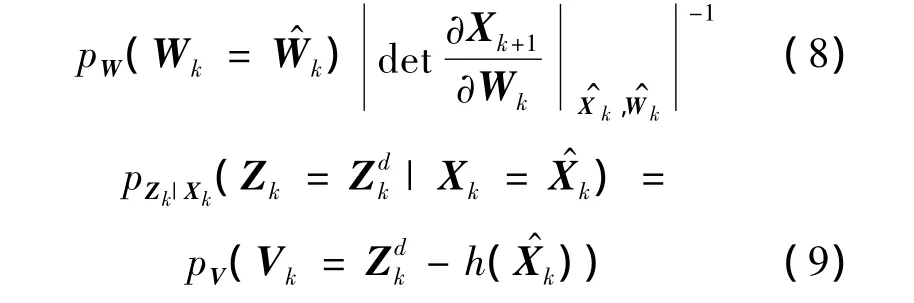
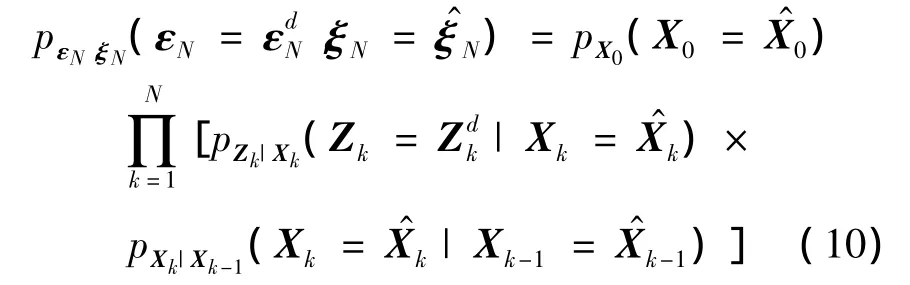
将式(8)、式(9)代入式(10)可得到:

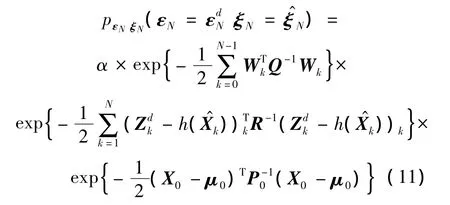
其中α为常量.

通过上述步骤就把在非线性高斯系统假设下的最大后验估计转化成了一个优化问题.问题的的形式如下:

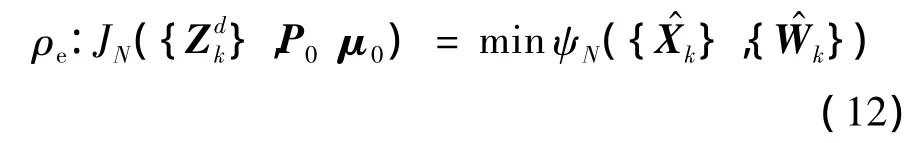
其中

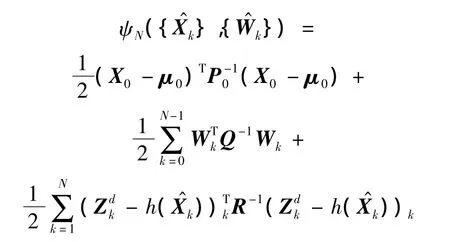
此优化问题将采用动态规划方法进行求解.动态规划是解决多级决策过程最优化的一种数学方法，是根据一类多级决策问题的特点，把多级决策问题变换为一系列互相联系的单级决策问题，然后逐个加以解决.

下面将用正向动态规划算法求解非线性系统模型下状态量的最优估计［10］.

由式(12)可知，非线性高斯系统假设下0～k时刻的总代价函数为

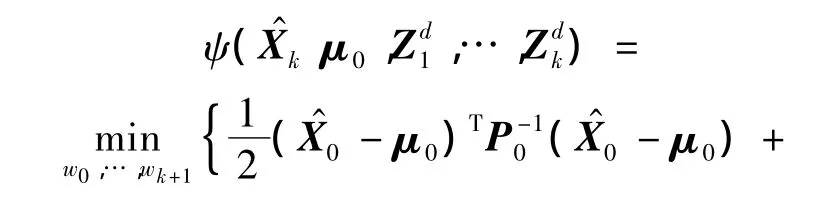
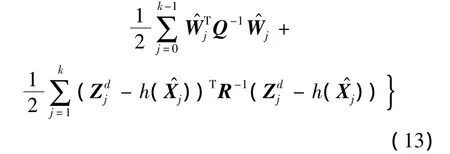
其中

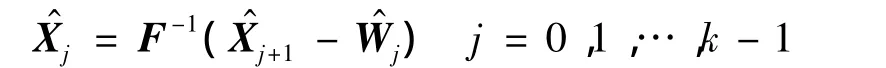
定义0时刻的部分代价函数为

用动态规划方法可得1时刻的部分代价函数的表达式:

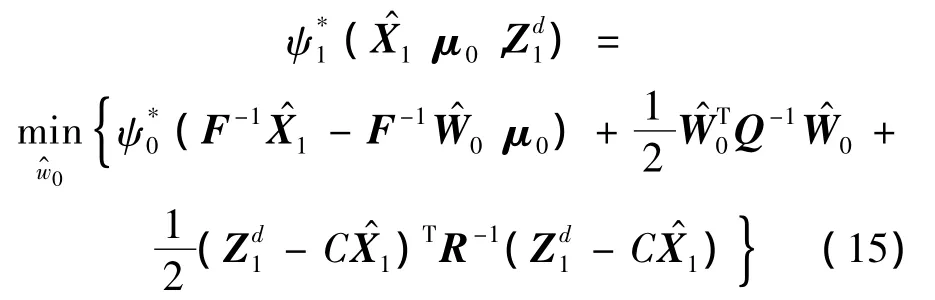
对于k大于等于1的时刻，部分代价函数的表达式可表示为

这样，就把多阶段决策问题转化为一系列单阶段决策问题，利用各阶段之间的关系，逐个求解就可得到系统各个时刻状态量的最大后验估计值.

3 实验验证

为了验证算法的有效性，取EKF的滤波结果作为比较.仿真分析将分别以模拟产生的GPS测量伪距值、测量伪距率值以及实际环境中软件接收机产生的实际数据作为观测量.分别采用EKF、基于优化理论的定位解算算法进行滤波.

首先验证基于优化理论的定位解算算法的有效性，接收机运动状态具体描述如下:

GPS测量伪距、伪距率模拟器初始位置为东经116.34°，北纬39.98°，高度102.97m，以20m/s向东匀速行进.数据输出频率1Hz.观测噪声为高斯噪声，伪距量测噪声方差为3.0×3.0m2，伪距率量测噪声为0.1 ×0.1(m/s)2.

基于优化理论的最大后验估计算法对数据处理后的误差波形图如图1～图5所示.

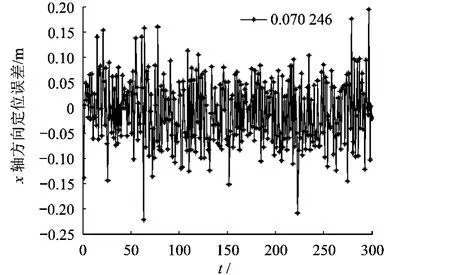
图1 x轴方向定位误差

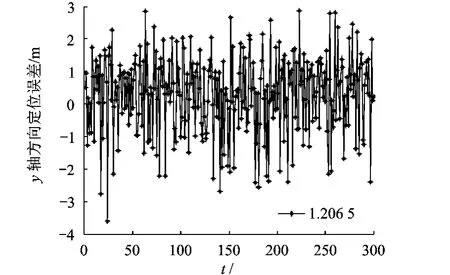
图2 y轴方向定位误差

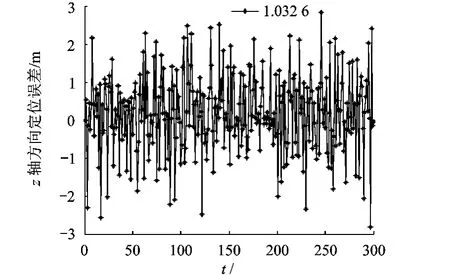
图3 z轴方向定位误差

下面分别利用EKF、基于优化理论的定位解算算法对数据进行滤波估计以实现定位，并对定位结果进行比较分析.

此项实验的软件接收机运动状态具体描述如下:

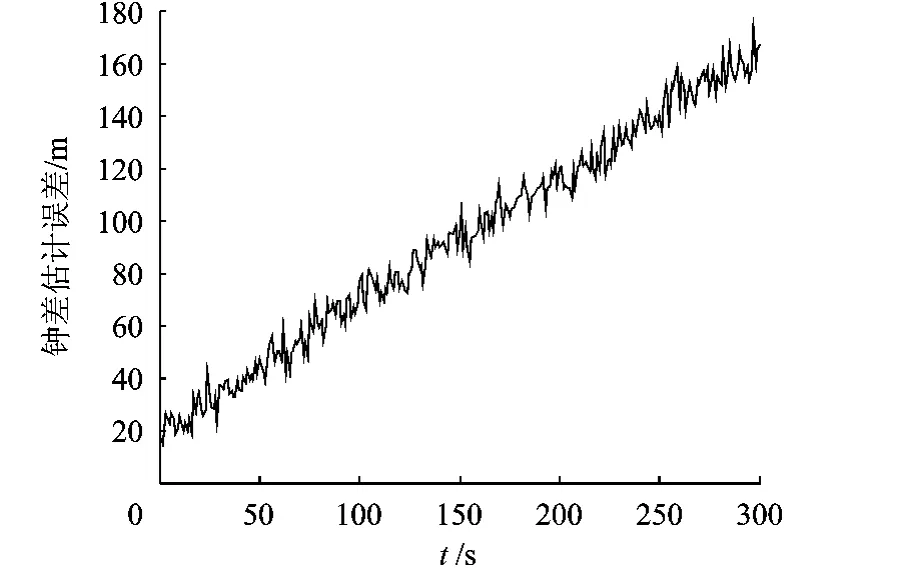
图4 钟差估计误差

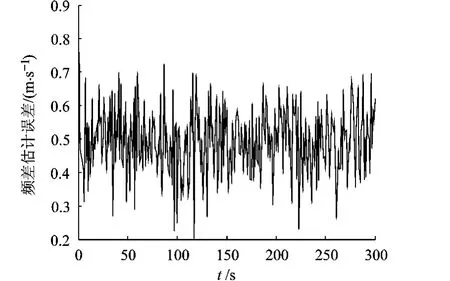
图5 频差估计误差

GPS软件接收机初始位置为东经116.34°，北纬 39.98°，高度 73.21m，接收机状态静止.数据输出频率1Hz.观测噪声为高斯噪声.实验数据为实际环境中软件接收机接收卫星信号后经过数据处理测得的伪距值、伪距率值.

EKF和基于优化理论的最大后验估计算法对数据处理后的误差波形图如图6～图8所示.

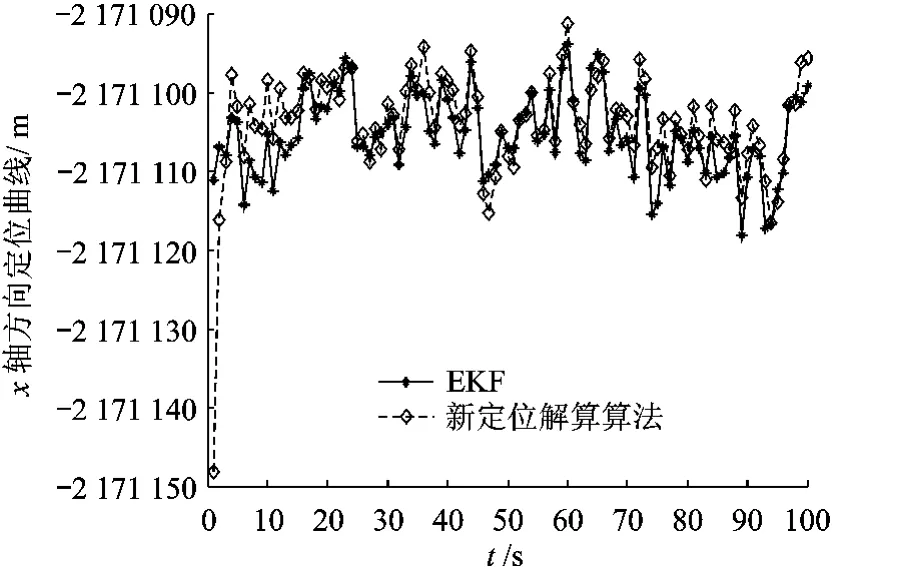
图6 x轴方向定位曲线

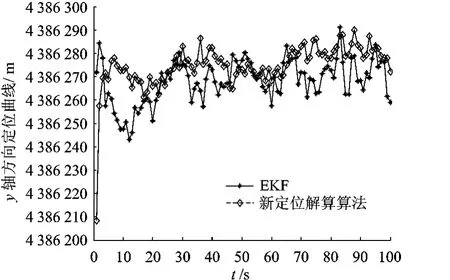
图7 y轴方向定位曲线

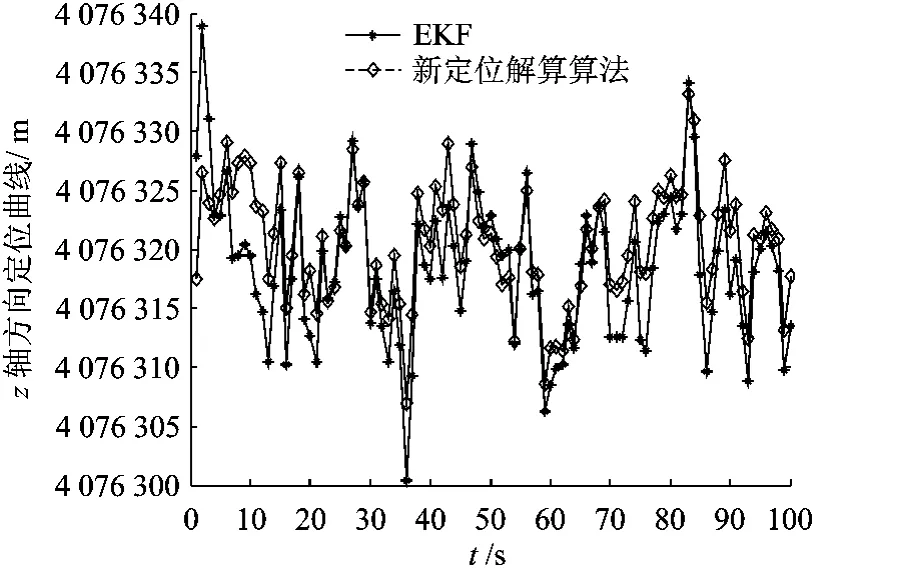
图8 z轴方向定位曲线

两种滤波方法在高斯噪声下的统计特性如表1所示.

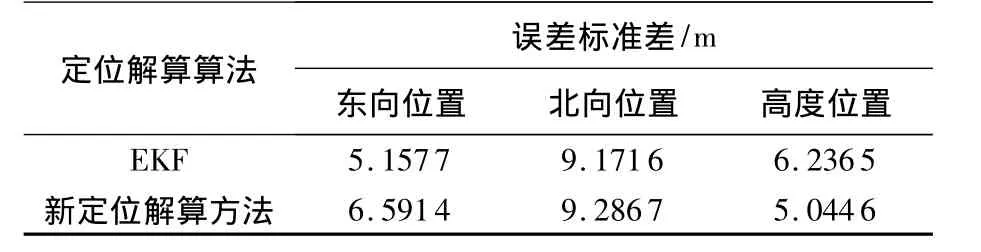
表1 两种滤波方式定位结果误差对比

由上面的实验结果可以看出，基于优化理论的最大后验估计算法在x，y轴方向定位精度要略低于EKF，在z轴方向上的定位精度要略高于EKF.

4 结束语

本文基于优化理论的思想，提出了一种新的定位解算算法.该方法采用优化理论的思路求解系统状态量的最大后验估计值.仿真实验的结果表明:该方法在拥有较高精度的同时采用一种非线性的估计方法进行定位解算，能完全解决定位解算中的非线性问题.

References)

［1］ Zhang Haitao，Zhao Yujiao.The performance comparison and analysis of extended Kalman filters for GPS/DR navigation［J］.OPTIK，2011，122(9):777 －781

［2］ Hong Deng，Liu Guangbin，Chen Haoming，et al.Application of EKF for missile attitude estimation based on"SINS/CNS"integrated guidance system［C］//Systems and Control in Aeronautics and Astronautics(ISSCAA).Harbin:IEEE Press，2010:1101 －1104

［3］ Christiand C，Lee Yu-Cheol，Yu Wonpil，et al.Augmented EKF localization for mobile robots in urban environments［C］//IEEE International Conference on Robotics and Biomimetics.Tianjin:IEEE Computer Society，2010:986 －991

［4］ Karlekar J，Zhou S Z，Lu Weiquan，et al.Positioning，tracking and mapping for outdoor augmentation［C］//IEEE International Symposium on Mixed and Augmented Reality(ISMAR).Seoul:IEEE Press，2010:175 －184

［5］ Steven M Kay.统计信号处理基础:估计与检测理论［M］.北京:电子工业出版社，2003:182－226 Steven M Kay.Fundamentals of statistical signal processing，volume I:estimation theory and volume П:detection theory［M］.Beijing:Electronics Industry Press，2003:182 － 226(in Chinese)

［6］ Pratap Misra，Per Enge.全球定位系统:信号、测量与性能［M］.2版.北京:电子工业出版社，2008:112－173 Pratap Misra，Per Enge.Global positioning system:signals，measurements，and performance［M］.2nd ed.Beijing:Electronics Industry Press，2008:112 －173(in Chinese)

［7］ Jame Bao-Yen Tsui.全球定位系统软件接收机基础［M］.2版，北京:电子工业出版社，2007:6－10 James Bao-Yen Tsui.Fundamentals of global positioning system receivers a software approach［M］.2nd ed.Beijing:Electronics Industry Press，2007:6 － 10(in Chinese)

［8］荆海英.最优控制理论与方法［M］.2版，沈阳:东北大学出版社，2002:73－102 Jing Haiying.Optimal control theory and methods［M］.2nd ed.Shenyang:Northeastern University Press，2002:73 －102(in Chinese)

［9］ Graham C Goodwin，María M Seron，José A De Doná.Constrained control and estimation［M］.London:Springer Press，2001:187－215

［10］李国勇.最优控制理论及参数优化［M］.北京:国防工业出版社，2006:118－137 Li Guoyong.Optimal control theory and parameter optimization［M］.Beijing:National Defence Industry Press，2006:118 －137(in Chinese)