基于参数矩阵计算全体极小碰集的方法

王 冬 冯文全 李景文 赵 琦

(北京航空航天大学 电子信息工程学院，北京 100191)

计算极小碰集是基于模型诊断的关键步骤之一［1－2］.极小碰集问题已被证明是非决定性多项式(NP，Non-deterministic Polynomia)完全问题，其难度决定了对该问题的算法研究只能是近似计算，不存在固定参数可解的算法［3］.目前大部分极小碰集算法都是从参数计算理论出发［3－4］，对一般化的问题加上权值或赋予其它约束，如限制碰集维度和各元组维度，从而寻找降低时间复杂度的方法.但在基于模型诊断中，冲突集的维度和诊断解的维度是不确定的，过多限制反而对诊断效果不利，因此针对这个实际问题，研究一般化的极小碰集求解算法是非常必要的.

极小碰集求解算法大致可分为:基于碰集(HS，Hitting Set)树［5－8］、基于布尔代数［9］、基于智能理论［10］等方法，各类算法的优劣已经过广泛的讨论.HSSE(Hitting Set-Set Enumeration)算法［11］解决了传统HS树在剪枝过程中丢失解的问题，但运算量随着问题规模而急剧增加，且对数据的规律性依赖过强，不适合用于大型系统诊断;BNB-HSSE(Branch and Bound-HSSE)算法［12］在HSSE基础上结合了分支界定法，将问题逐步分解，但其参数化的求解方式使分支树反复生成，增加了计算复杂度;基于二维数组结构［13－14］的算法避免了使用搜索树，易于编程实现，但由于其本质上属于枚举法，因此计算效率不高.此外在大型系统诊断中，状态空间规模的增加会使算法性能急剧恶化，甚至无法诊断，因此进行大规模计算时的求解效率也是衡量算法的重要标准之一.

本文提出的M-MHS(Matrix-based Minimal Hitting Set)算法，利用参数矩阵描述元素与集合的关系，通过矩阵分解和有效的剪枝规则进行求解，不仅能够求出全体极小碰集，且在进行较大规模计算时具有明显优势，为大型系统基于模型诊断提供了可行方法.

1 问题描述

定义1 称H为集合簇 S={ci，i=1，2，…，N}的碰集，当且仅当 H⊆U(U=∪ci={e1，e2，…，em}，表示集合簇中所有元素的集合.数目为m)，并且对每一个ci∈S，都有H∩ci≠∅.若H的任意真子集都不是碰集，则它是极小碰集(MHS).

定义2 定义m×n参数矩阵，其中m为冲突集合簇中包含元素的个数，n为冲突集合簇中包含冲突的个数.矩阵中第i行第j列位置的值表示第j个冲突是否包含第i个元素，是为1，否为0.

参数矩阵描述了元素与冲突的关联关系，可以得到以下推论:

推论1 若矩阵的某一行为全1，则该行对应的元素是一个极小碰集.

推论2 若矩阵的某一行为全0，则该行对应的元素不可能出现在极小碰集中.

推论3 若参数矩阵的某一列为全0，则该问题无碰集解;若矩阵没有全0列，则该问题一定有解.反之也成立.

2 算法描述

基于参数矩阵的极小碰集计算算法通过判断矩阵中0，1元素出现的次数和位置，快速将原始问题分解为一系列子问题，并且在进行碰集判断时利用上述3个推论，简化了传统搜索算法中集合覆盖的判断过程，大大提高了求解效率.

2.1 M-MHS 算法

1)输入参数矩阵Mm×n和用于存储计算结果的列表H;

2)删除全0行;

3)统计各元素在冲突集中出现的次数，即各行包含1的个数;

4)若当前参数矩阵不为空，则取出当前出现次数最多的元素及矩阵中对应的行;若为空，则转9);

5)若该行为全1行，则加入H，并删除该行，返回4);

6)若该行包含0，则分解矩阵.若该行第i个值为1，则删除参数矩阵中对应的列，若为0，则保留这一列.假设该行包含k个0，可以得到一个新的矩阵M'm×k;

7)输入 M'm×(n－k)和 H'，递归调用算法 MMHS;

8)删除该行，并将H'归并于H，返回4)或转9);

9)返回H.

2.2 参数矩阵分解方法

M-MHS算法是递归调用的，根据不同的参数矩阵计算相应的极小碰集.除初始参数矩阵由冲突集合簇计算得出，其余各矩阵都是在初始矩阵基础上根据扩展元素进行分解的结果.分解的方法为:

矩阵1 记录扩展元素所在行中所有0值的位置，并从初始矩阵中提取这些0值所属的列，合并为一个新矩阵，即 M'm×(n－k).

矩阵2 初始矩阵中删除扩展元素所在行，即执行步骤8)后的结果.

通过上述方法，初始问题被分解为两个子问题.根据参数矩阵中0，1所表示的意义，可知该分解思想类似于分支定界树搜索中的二叉扩展，两个子问题对应于元素在碰集中和元素不在碰集中.但由于M-MHS算法在分解时考虑了各元素在冲突集簇中出现的频率，因此能够更快地计算出碰集.

2.3 剪枝规则

为了避免非极小碰集的产生，将H'归并于HS时需加入剪枝规则:

1)对H'中的某个碰集h，若H中存在它的子集，则放弃h;

2)对H'中的某个碰集h，若H中存在它的超集，则用h代替它的超集;

3)若H'列表为空，则直接退出本次循环.即在该子问题中，所有出现次数小于等于当前扩展元素的元素，都不可能构成碰集.

M-MHS算法考虑了各元素在冲突集簇中出现的次数，同时又使用了剪枝规则，这样不仅保证了计算出的碰集是极小的，且能够及早避免对无解子问题的计算，因此在求解效率上较以往算法有很大提高.

3 系统仿真验证

3.1 算例分析

给定冲突集合簇 S={{B，D，E}，{A，B，C}，{A，C，E}，{B，D，F}，{B，D}，{B，C，E}，{A，F}}，求解极小碰集.

1)参数矩阵增加一列为统计各元素在冲突集簇中出现的次数，可得初始参数矩阵为

2)首先扩展元素B.由于该行不是全1行，取出0值对应的列.删除全0行并统计各元素出现的次数，可得

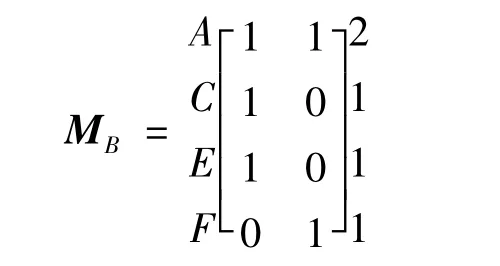
①扩展元素A，由于该行为全1行，直接加入碰集列表HB={{A}}，并删除A行;

②元素C，E，F出现次数相等，随机选择一个进行扩展，假设扩展C，可得参数矩阵:

F行为全1行，因此加入碰集列表HBC={{F}}，将其与扩展元素C合并可得碰集{{C，F}}，删除C行.

③ 碰集列表HB={{A}，{C，F}}.继续扩展元素E，可得参数矩阵:

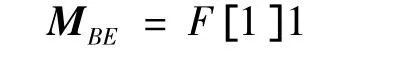
F行为全1行，因此加入碰集列表HBE={{F}}，将其与扩展元素E合并可得碰集{{E，F}}，删除E行.

④ 碰集列表 HB={{A}，{C，F}，{E，F}}.继续扩展元素F，得到的参数矩阵为空，因此包含元素B的碰集求解完毕.将碰集列表HB合并扩展元素 B，可得 H={{B，A}，{B，C，F}，{B，E，F}}，并删除B行;

3)元素A，C，D，E出现次数相等，随机选择一个进行扩展，假设扩展A，可得参数矩阵:

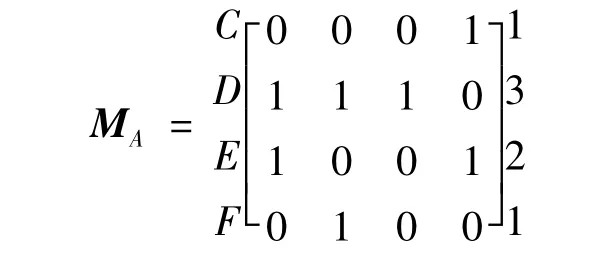
①扩展元素D，可得参数矩阵:

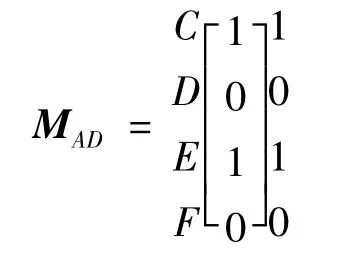
删除M'AD中全0行，C，E行都是全1行，因此HAD={{C}，{E}}，将其与扩展元素D合并可得HA={{D，C}，{D，E}}，删除 D 行.

②扩展元素E，可得参数矩阵:

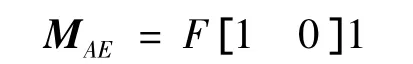
矩阵中包含全0列，因此HAE≠∅.根据剪枝准则3)，出现次数小于元素E的C，F都无需扩展，包含元素A的碰集求解完毕.将碰集列表HA合并扩展元素 A，可得 H={{B，A}，{B，C，F}，{B，E，F}，{A，D，C}，{A，D，E}}，删除 A 行.

4)同理，扩展元素C可得H={{B，A}，{B，C，F}，{B，E，F}，{A，D，C}，{A，D，E}，{C，D，F}}，删除C行.

5)继续扩展元素D，可得HD≠∅.根据剪枝准则3)，出现次数小于元素D的E，F都无需扩展.循环至此退出.

6)返回极小碰集列表 H={{B，A}，{B，C，F}，{B，E，F}，{A，D，C}，{C，D，F}}.

按照HSSE方法求得的结果与上述结果相同，从而验证了该算法的正确性.

3.2 统计分析

采用Visual C++6.0编程实现了M-MHS算法，并在 Intel Core2 Duo CPU 2.66 GHz 1.95 GB内存，Windows XP操作系统下运行.用于实验的比对数据分为3组:随机数据、有规律数据、不同规律数据.

为了验证该算法的效率，比较了HSSE和修改的BNB-HSSE两种算法的计算结果.其中对BNB-HSSE算法的修改有2个方面:

1)取消了上下界计算;

2)修改了节点是否分支的判断条件.

这两处修改主要为了去除原BNB-HSSE算法中参数化的影响，使之能够从通用碰集计算的角度进行求解，仿真结果如下.

3.2.1 随机数据

集合簇个数和元素总数都为n，每个集合的长度和包含元素为随机产生，但元素没有重复.表1为集合簇个数从20递增到40时3种算法的运行时间比较.

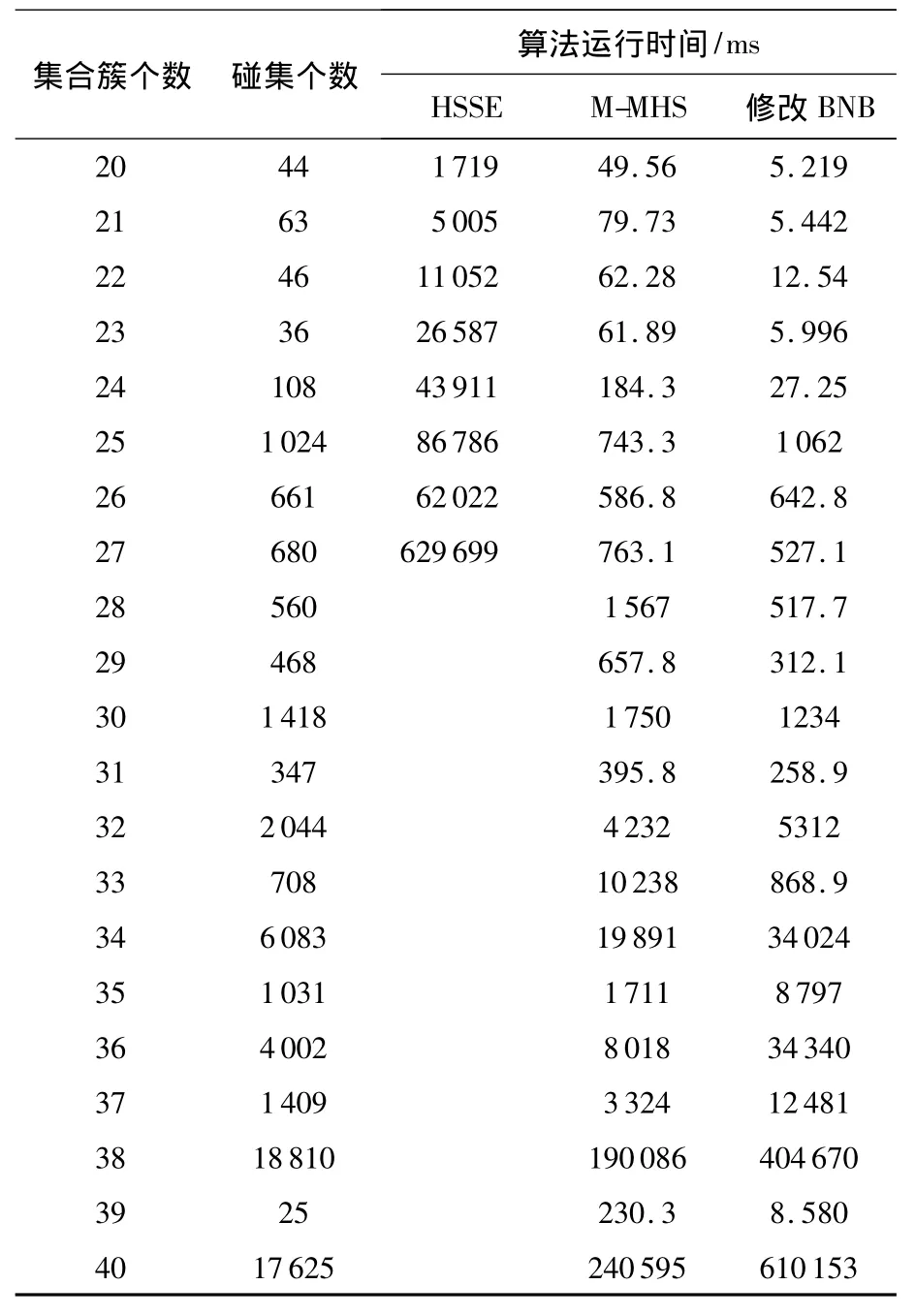
表1 随机数运行时间比较

可以看出，M-MHS和修改后的BHB-HSSE算法的性能要优于HSSE.当集合簇个数大于27时，HSSE的枚举过程耗时严重，而另外两种算法仍可以在较短时间内求解.当碰集个数较多时，M-MHS的性能要优于修改后的BHB-HSSE算法，而当碰集较少时，修改后的BHB-HSSE能够在更短时间结束运算.

3.2.2 有规律数据

集合簇个数为 n，各集合分别为{1，2，…，n}，{2，3，…，0}，…，{n，0，…，n －2}.图 1 为集合簇个数从35递增到60时3种算法运行时间比较.

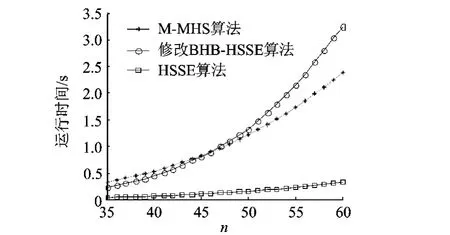
图1 有规律数运行时间比较

可以看出，HSSE算法的运行时间要大大少于M-MHS算法和修改后的BHB-HSSE算法，这主要得益于数据的规律性.由于对于元素集合内的任一元素，至少会在n个集合簇中会出现n－1次，因此所有双元素集合都是碰集，所有三元素集合都不是极小碰集.而HSSE算法由空集到全集按宽度优先扩展，求解极小碰集时只需扩展到第2层，因此在这种情况下，HSSE枚举树中的节点有用率非常高，求解速度很快.

M-MHS和修改后的BHB-HSSE算法的运算速度在集合簇个数等于47时发生了翻转.当碰集个数较少时，修改后的 BHB-HSSE性能优于M-MHS，而碰集个数较多时，M-MHS的运算时间更短.

3.2.3 不同规律数据

集合簇个数为固定值n，各集合分别为{1，2，…，n －i}，{2，3，…，n － i+1}，…，{n，1，…，2n －i}，其中i＜n为可变参数，决定了各集合的维度.仿真中集合簇个数为50，i为［0，10］.3种算法运行时间比较如图2所示.

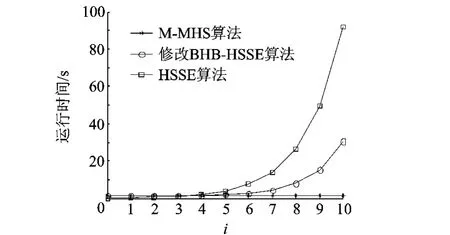
图2 不同规律数运行时间比较

随着i的增长，HSSE和修改后的BHB-HSSE算法性能下降明显，而M-MHS算法的运行时间始终维持在一个比较稳定的范围内.因为对M-MHS算法而言，初始参数矩阵大小是不变的，变化的只是各行中0，1值的个数，因此矩阵分解所用总的时间波动不大.而对于基于分支的BHB-HSSE算法，随着i的增加，扩展产生的“不包含某元素的集合列表”分支中集合个数越来越多，相应地搜索树也会越来越复杂，因此求解时间受搜索树规模影响呈指数增长.

从上面仿真结果可以得出，当集合簇和元素个数越多时，M-MHS算法明显具有计算效率上的优势，且当数据按不同规律变化时，算法性能仍维持相对稳定.因此M-MHS算法能够适用于大型系统诊断.

4 结束语

本文提出了一种基于参数矩阵计算极小碰集的M-MHS算法.该方法利用参数矩阵描述元素与集合簇的关系，通过矩阵分解将原始问题逐步分解为多个子问题，并采用有效的剪枝规则避免对无解子问题的计算，从而提高了效率.仿真结果表明:该算法在进行较大规模碰集计算时具有明显优势，且对不同规律数据能够维持性能稳定，从而为实现大型系统基于模型诊断提供了可行方法.

References)

［1］ de Kleer J，Williams B C.Diagnosing multiple faults［J］.Artificial Intelligence，1987，32(1):97 －130

［2］ Williams B C，Ragno R J.Conflict-directed A*and its role in model-based embedded systems［J］.Discrete Applied Mathematics，2007，155(12):1562 －1595

［3］李绍华，王建新，冯启龙，等.Set Cover和 Hitting Set问题的研究进展［J］.计算机科学，2009，36(10):1 －4 Li Shaohua，Wang Jianxin，Feng Qilong，et al.Set cover and hitting set:a survey［J］.Computer Science，2009，36(10):1 － 4(in Chinese)

［4］蔡烜.d-Hitting Set问题的固定参数化算法［D］.上海:上海交通大学计算机科学与工程系，2009 Cai Xuan.Fixed-parameter algorithms for d-Hitting set problems［D］.Shanghai:Department of Computer Science and Engineering，Shanghai Jiao Tong University，2009(in Chinese)

［5］ Reiter R.A theory of diagnosis from first principles［J］.Artificial Intelligence，1987，32(1):57 －95

［6］ Wotawa F.A variant of Reiter's hitting-set algorithm［J］.Information Processing Letters，2001，79(1):45 － 51

［7］ Greiner R，Smith B A，Wilkerson RW.A correction to the algorithm in Reiter's theory of diagnosis［J］.Artificial Intelligence，1989，41(1):79 －88

［8］姜云飞，林笠.用对分HS—树计算最小碰集［J］.软件学报，2002，13(12):2267 －2274 Jiang Yunfei，Lin Li.Computing the minimal hitting sets with binary HS-tree［J］.Journal of Software，2002，13(12):2267 －2274(in Chinese)

［9］姜云飞，林笠.用布尔代数方法计算最小碰集［J］.计算机学报，2003，26(8):919 －924 Jiang Yunfei，Lin Li.The computing of hitting sets with boolean formulas［J］.Chinese Journal of Computers，2003，26(8):919 －924(in Chinese)

［10］黄杰，陈琳，邹鹏.一种求解极小诊断的遗传模拟退火算法［J］.软件学报，2004，15(9):1345 －1350 Huang Jie，Chen Lin，Zou Peng.A compounded genetic and simulated annealing algorithm for computing minimal diagnosis［J］.Journal of Software，2004，15(9):1345 － 1350(in Chinese)

［11］ Zhao Xiangfu，Ouyang Dantong.A method of combining SE-tree to compute all minimal hitting sets［J］.Progress in Natural Science，2006，16(2):169 －174

［12］陈晓梅，孟晓风，乔仁晓.基于BNB-HSSE计算全体碰集的方法［J］.仪器仪表学报，2010，31(1):61 －67 Chen Xiaomei，Meng Xiaofeng，Qiao Renxiao.Method of computing all minimal hitting set based on BNB-HSSE［J］.Chinese Journal of Scientific Instrument，2010，31(1):61 － 67(in Chinese)

［13］林笠.基于模型诊断中用逻辑数组计算最小碰集［J］.暨南大学学报:自然科学与医学版，2002，23(1):24－27 Lin Li.Computing minimal hitting sets with logic array in model-based diagnosis［J］.Journal of Jinan University:Natural Science ＆ Medicine Edition，2002，23(1):24 －27(in Chinese)

［14］ Fijany A，Vatan F.New approaches for efficient solution of hitting set problem［C］//Proceedings of the Winter International Symposium on Information and Communication Technologies.Cancun，Mexico:Trinity College Dublin，2004