大地电磁多站叠加系统的分辨率误差分析

蒋 礼

(1.中国地质大学(武汉)地球物理与空间信息学院,武汉430074;

2.华北水利水电学院 数学与信息科学学院,郑州450011)

1 引 言

由于天然电磁场非常微弱,使用传统大地电磁观测系统所采集的有用信号往往都淹没在各种地质噪声和人文噪声中。随着国家工业化的发展,以往比较理想的观测点也出现了大量的人文噪声。远参考、robust 等大地电磁传统算法,对于能量较强、覆盖范围较广且持续较长时间的相关噪声无法有效予以滤除[1-2]。多站叠加技术具有从纷繁复杂的噪声环境中提取极其微弱有效信号的超强能力[3],20 世纪80 年代Pedersen 就提出了进行大地电磁多站观测的设想[4],但在当时并未引起人们的注意。主要原因是因为该方法虽然可以有效提高信噪比,但却有可能降低大地电磁响应的分辨率。一旦多站叠加造成的误差过大,反而会降低数据观测质量,进而得到错误的反演结果,最终造成巨大的经济损失。

本文设计了一个基本的二度异常体模型,采用计算机模拟仿真的方法成功获取了大地电磁多站叠加的观测结果。将多站叠加结果与理论值进行对比,可以分析大地电磁多站叠加系统的误差大小。调整该模型的参数,可以得到在不同地质条件下的大地电磁多站叠加系统的误差变化规律。对于上述结果进行系统分析可以发现,只要设置合适的台站间距,使用多站叠加技术并不会明显降低大地电磁响应的分辨率。

2 原理简介

2.1 大地电磁理论

大地电磁是利用天然电磁场源探测地球深部结构的一种科学理论[2,5],其基本原理公式如下:

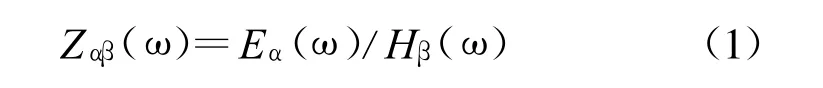
式中, ω表示角频率,Eα和Hβ分别代表着在垂直对应方向上在地表所观测到的电场分量和磁场分量。由于电场的单位为V/m,而磁场单位为A/m, 两者相除得到电阻单位Ψ,所以Zαβ(ω0)可以看作是测点至趋肤深度这段距离内的介质在某一极化方向上的电阻值。从式(1)可以看出,阻抗值是一个随频率变化的量。当角频率确定为某一值如ω0时,则该频率的阻抗值Zαβ(ω0)反映了由地表开始到该频率电磁波的趋肤深度为止的这么一段地下介质的电性结构。所以理论上只要在地表记录下任意频率的电场和磁场数据,那么就可以了解到地下所有深度的电性结构[2]。

2.2 多站叠加系统

假设在某一测点进行大地电磁观测时,在该标准点O 的附近,设置了N 个辅助台站用以进行多站叠加。假设在地表标准点所记录的电场和磁场分别为EOα和HOβ,第i 个辅助观测台站所记录的电场和磁场分别为Eiα和Hiβ,根据公式(1),由标准点的观测数据所估算的阻抗值为

而由所有辅助测站观测到的数据进行多站叠加所估算得到的阻抗值为

式中,we和wh分别为电场和磁场的归一化多站叠加权系数,即:∑e=∑wh=1。

由于地下介质的非均匀性会引起地表不同测点的阻抗值产生变化,对于阻抗曲线而言,可能会出现极值、拐点、上升或下降等变化趋势,这种变化是对地下介质结构的一种精确刻画。然而,在进行多站叠加的过程中,由于引入了相邻测点的信息,使得多站叠加值Zsupαβ和真实值ZOαβ之间存在差异。所以大地电磁多站叠加技术可能会在真实阻抗曲线上引入误差、产生畸变,从而降低了大地电磁方法的分辨率。

2.3 分析方法与研究重点

通过对比ZOαβ和Zsupαβ 两者结果之间的差异,可以获得大地电磁多站叠加技术相较于传统大地电磁理论,对于地下介质分辨率的变化趋势和变化规律。由大地电磁测深理论的物理机制可知,影响大地电磁多站叠加分辨率的因素非常多,如异常体的埋深、辅助台站的站间距、地下电性结构等,甚至于在地表的不同位置、不同频率的结果之间,也可能存在很大的区别。

鉴于该问题在理论上的复杂性,以及考虑到野外施工的具体特点,本文将主要研究并解决以下几个方面的疑问。

(1)台站的间距

设置较远的台站间距可以有效降低不同台站间噪声的相关性,但同时又会降低各台站有效信号的相似性。那么在野外施工时,对于地下地质结构不明的情况,是否存在一个安全的台站间距?

(2)不同的异常体

由于在地下介质中,异常体的形状、电性参数和埋深的不同,即使两个相距很近的观测台站,也有可能获得差异较大的有效信号。那么不同的异常体将会对大地电磁多站叠加技术的分辨率产生什么影响?

(3)不同频率的结果

即使对于同样的地质结构,以相同的台站间距进行多站观测,由于不同频率电磁波的穿透深度不一样,阻抗结果也可能在不同的频点呈现不同的差异。那么对于不同的勘探深度,多站叠加的分辨率将呈现什么样的变化规律?

3 仿真实例

下面将参照Poll 的理论[6],基于有限差分的方法,使用Fortran 语言模拟实现大地电磁多站叠加的过程,并得到相应的数值解结果。

3.1 模型建立

3.1.1 地质结构

仿真模型的三维立体图如图1(a)所示,本文设计了一个典型的陡坎电性不均匀体模型[5]。一来,由于陡坎模型的物理构造简单,所以使用陡坎会大大降低仿真程序的难度;二来,因为无论是地垒、地堑,还是形状复杂的异常嵌入体,都可以看作是由多个陡坎模型组合而成,所以使用陡坎并不会降低结论的普适性。多站观测系统的设置方式如图1(b)所示,其中O 点为理论测点,在以该点为圆心、R 为半径的圆周上,均匀布设多个观测台站组成多站观测系统。在仿真实例中为了简化程序,将多站观测系统缩减为3 个台站组合(3 个观测台站A、B、C 在测点O 周围均匀分布)。h1是陡坎隆起一侧至地表的距离(也即埋深),h2是陡坎的高度,整个模型的深度为H(见图1(c))。陡坎上方介质的电导率为σ1,下方介质的电导率为σ2,且直角坐标系的原点位于陡坎的正上方(见图1(d))。Z =0 相当于地表,也即测站所在的平面,陡坎沿X 走向延伸,施工时将沿Y 方向布设测站来获取阻抗曲线(见图1(e))。

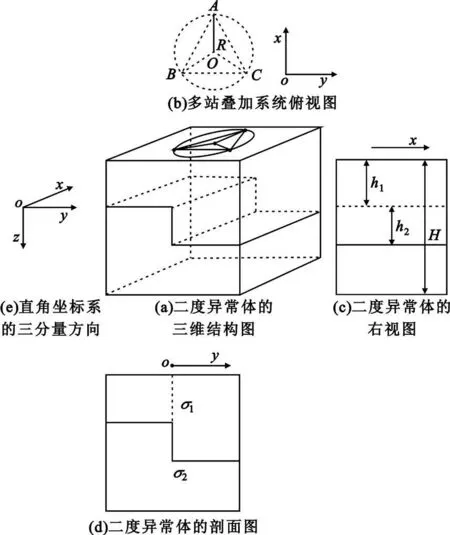
图1 地质结构模型Fig.1 Geological structure model

3.1.2 电性参数

为了分析不同地下介质对于多站叠加系统分辨率的影响,对图1 的地质结构模型设计不同的物性参数可得到多个子模型。在所有子模型中,模型的总体深度H 和陡坎高度h2不变, 均为500 km和5 km,但陡坎将呈现1 km、5 km和10 km 3 种不同的埋深情况。在子模型I、II、III 中,陡坎的上方为高阻体,下方为低阻体;而子模型IV、V、VI 则完全相反。另外,为了增加最终结论的普适性,将高阻体和低阻体的电导率分别设为0.001 s/m和1 s/m这种比较极端的情况,这样多站叠加将会放大分辨率的误差。所有子模型的参数见表1 所示。

表1 模型参数Tab le 1 Model′s parameters

3.1.3 实验方案

基于仿真模型,对于大地电磁多站叠加系统进行分辨率误差研究的具体实验方案如下:在二度异常体的地表布设多个观测台站,记录下所有测点单站观测的结果作为地下结构在地表反映的真实电性值,然后在每个单站测点的附近布设下另外3 个辅助观测站,并将此3 个辅助台站的观测结果作为该测点的多站观测值;将每个测点的多站观测值与理论真实值的阻抗估算结果进行对比分析,以总结不同模型、不同频段、不同间距的多站组合方式在地表不同观测点的分辨率变化规律。

3.2 仿真结果

3.2.1 阻抗曲线

由于根据公式(2)、(3)所求得的阻抗值为复数,为了显示方便,通常将其转换为视电阻率和相位两个实数值[7]。将陡坎上方的不同位置测点在同一频率的视电阻率值(或相位值)组合在一起,就可以得到一条完整的电性结构曲线。由模型I 绘制出的1 000 Hz阻抗曲线如图2 所示,其中图2(a)为视电阻率曲线,而图2(b)为相位曲线。图中实线为真实的阻抗曲线,虚线表示多站叠加的结果,不同线型代表着不同的站间距。从图2 可以看出,无论是视电阻率还是相位曲线,都能准确无误地反映出地下介质的陡坎畸变(Y =0 附近)。

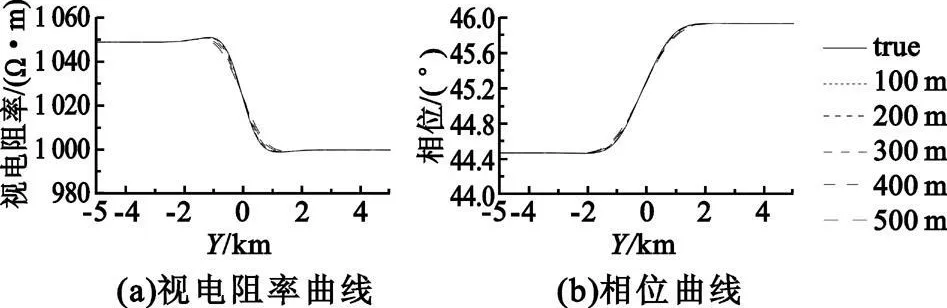
图2 模型I 的阻抗曲线(1000 Hz)Fig.2 Impedance curve of the model I(1000 Hz)

根据模型I 的表层电阻率可以计算出趋肤深度约为500 m,即此频率的电磁波尚未穿透表层,所以在图2 中视电阻率依旧呈现高阻值(在1 000 Ψ·m左右)。由于在不同电导率介质的分界面上会有电荷积累,由此产生的电场也将被表层的测站所记录,这就造成了Y 轴左右两侧电阻率值的差异。从图2中可以看出,当阻抗值随测站位置变化较为剧烈时,往往误差值较大;而且随着站间距的增加,误差值变得越来越大。

3.2.2 误差曲线

当地下介质的电性差异很大的时候,不同频率的阻抗值也将呈现很大的区别。如果多站叠加产生了几欧姆米的误差,其对于高阻层而言不会有太大影响,但对于低阻层却影响巨大,这可能会对地质构造做出完全错误的判断。相对误差概念更加适合地质反演解释,能够更准确地刻画大地电磁测深分辨率的变化情况。基于图1 的地质模型, 根据公式(2)、(3)可以得到理论阻抗值ZOαβ和多站叠加的阻抗值Zsupαβ,则相对误差定义为

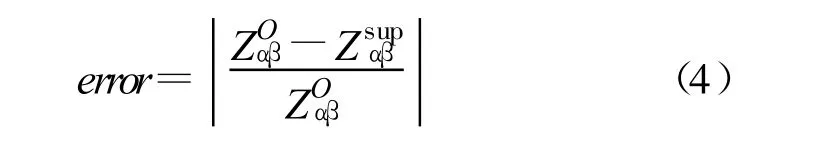
将模型的电性参数(见表1)代入仿真程序,可以得到地表任意测站在不同频段所记录到的电磁场值,根据公式(2)、(3)和(4),可以获取地表任意测点在不同频段的多站叠加相对误差值。可以看出,误差值随着站点位置和频率值两个参数发生变化。为了叙述方便,下面对于这两个参数将分别绘制误差曲线。

(1)随站点位置变化的误差曲线

模型I 的多站叠加误差曲线如图3 所示。为了与图2 相对应,图3 依旧截取了Y 从-5 km到5 km合计10 km的结果。图中上方为视电阻率的误差,下方为相位的误差,不同的线型代表着由于不同的台站间距所引起的误差。由于篇幅有限,此处仅选择了3 个频点的误差值作图,从左往右频率值逐渐降低。从图3 中可以明显看出,就误差值的数量级而言,高频部分的误差值较小,而低频部分的误差值较大。

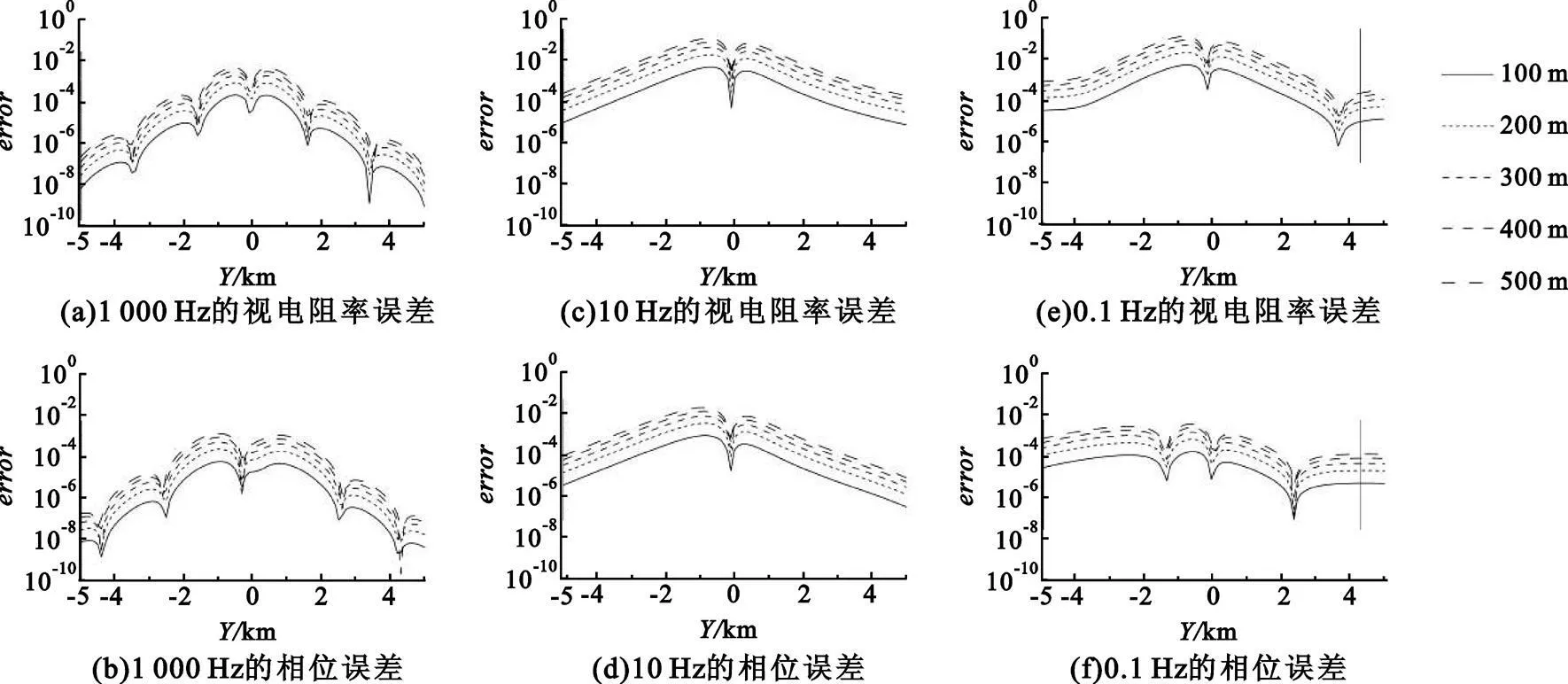
图3 模型I 在不同频率的多站叠加误差对比Fig.3 The comparison of multi-station superposition error of the model I at different frequency

(2)随频率变化的误差曲线

为了分析多站叠加误差随着频率的变化规律,特绘制图4。由于篇幅限制,此处依旧以模型I 为例作图。从图3 中可以看出,在陡坎阶跃处正上方的误差值一般较大,所以在图4 中,将选择Y 在0 km、+1 km和-1 km 3 个点位作图。

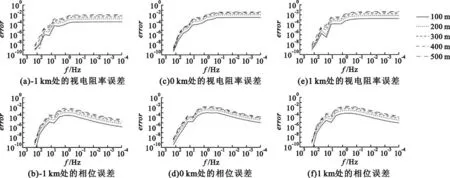
图4 模型I 在地表不同位置的多站叠加误差对比Fig.4 The comparison of multi-station superposition error of the model I in different position on surface

从图4 中可以明显看出,在地表不同点位所获得的误差结果虽然有所不同,但曲线整体的变化趋势还是较为一致。随着频率的逐渐降低,视电阻率误差越来越大,并最终趋向于一个稳定值;而相位误差则存在一个拐点,初始,随着频率的降低,相位误差越来越大,但经过拐点之后,误差值随着频率的降低而缓慢减小。

图5 所有模型在同一频率的多站叠加误差对比Fig.5 The comparison of multi-station superposition error of all models at the same frequency

(3)所有模型的误差对比

不同模型的误差对比结果见图5 所示,由于篇幅所限,所有模型均统一选取0.01 Hz的误差值进行绘图。从图中可以看出,无论是子模型I、II、III,还是子模型IV、V、VI,随着异常体埋深的逐渐增加,多站叠加的误差值越来越小。

3.3 多站叠加系统的误差分析

从图3、图4 和图5 的对比中可以看出,引起多站叠加误差的因素非常多,综合全部模型的所有误差结果,可以总结出以下规律。

(1)对于所有陡坎模型,增加台站间距都会使得误差变大。这主要是因为点位不同造成辅助台站的有用信号偏离了测点的真实信号,台站间距越大,辅助台站的有用信号与真实信号之间的差异将会越大。

(2)对于所有陡坎模型,高频部分误差会小于低频部分的误差。这主要是由大地电磁测深原理决定的:在电磁波没有穿透表层,且离异常体分界面较远时,误差值较小;当电磁波的趋肤深度接近异常体的埋深时,误差开始逐渐增大;随着低频电磁波的穿透深度越来越大,该误差最终趋向于一个稳定值。

(3)对于所有陡坎模型,异常体的埋深越浅,多站叠加可能产生的误差越大,尤其最终在低频部分,将可能呈现出较大的误差值。这主要是由于所有测站都位于地表,当其距离分界面越近时,所测得的异常场值也将越大。

(4)对于所有陡坎模型,在陡坎正上方地表数公里的范围内,可能会出现较大的误差。如果埋深较浅,则范围较小,但误差值较大;如果埋深较深,则范围较大,但误差值较小。这主要是因为在陡坎的跳变处,异常场的场强变化也变得较为剧烈。

(5)从本文的模型来看,电阻率的误差值一般大于相位的误差值。但是,当频率的穿透深度接近异常体的分界面时,相位的误差值会大于电阻率的误差值。该现象主要出现在相位误差的拐点频率附近。

4 结 论

通过对于陡坎模型的大地电磁多站叠加结果的误差分析,获得了不少的有用信息,这些信息对于具体的野外施工具有较高的参考价值。

(1)在进行大地电磁深部探测时,完全可以使用多站叠加的方法进行数据的采集与处理。对于任何情况,只要选择合适的台站间距,就能够将大地电磁的多站叠加误差值控制在合理的范围之内。

(2)对于大地电磁测深而言,台站间距设置得越小,由多站叠加引起的阻抗误差值也越小。对于埋深在1 km以内的不均匀体,300 m的台站间距可以保证任何情况下的最大误差值都不超过1%,这样完全不会影响到最终的勘测精度。

由于篇幅所限,本文仅详细讨论了大地电磁多站叠加结果在TM 极化模式下的阻抗误差变化情况。但由大地电磁的基本理论可知,对于浅层的不均匀体结构,TE 极化的多站叠加误差值必然小于TM 极化的多站叠加误差值[8]。对于某一多站观测方案而言,如果TM 极化的多站叠加结果都能满足观测任务的要求,那么TE 极化的多站叠加结果必定也能满足该观测任务的要求。

[1] Egbert G D.Processing and interpretation electromagnetic induction array data[ J] .Surveys in Geophysics, 2002, 23 (2-3):207-249.

[2] Simpson F, Bahr K.Practical Magnetotellurics [M] .New York:Cambridge University Press, 2005.

[3] Jiang Li, Xu Yixian.Comparisons of the magnetotelluric experimental results by Multi-site remote reference and Multi-site superposition[R] .Beijing:International Workshop on Gravity, Electrical &Magnetic Methods and Their Applications, 2011.

[4] Pedersen L B.Some aspects of magnetotelluric field procedures[J] .Surveys in Geophysics,1988,9(3-4):245-257.

[ 5] Kaufman A A,Keller G V.大地电磁测深法[M] .刘国栋,晋文光, 邓前辉, 等,译.北京:地质出版社,1987.

Kaufman A A, Keller G V.The magnetotelluric sounding method[M] .Translated by LIU Guo-dong, JIN Wen -guang, DENG Qian-hui, et al.Beijing:Geological Publishing House, 1987.(in Chinese)

[6] Weaver J T, Poll E H,Jones A G.Calculations of voltages for magnetotelluric modeling of a region with near-surface inhomogeneities[J] .Physics of the Earth and Planetary Interiors,1989, 53(3-4):287-297.

[7] Vozoff K.Magnetotellurics:Principles and practice [ J] .Earth Planet, 1990, 99(4):441-471.

[8] Berdichevsky M N.Marginal notes on magnetotellurics[ J] .Surveys in Geophysics,1999, 20(3):341-375.