一种新的卫星信号调制方式识别方法

杨 健,徐宏飞,陈 曦

(1.解放军73691 部队, 南京210014;2.南京理工大学 电子工程与光电技术学院,南京210094)

1 引 言

卫星通信凭借覆盖区域广、通信质量高的特点日益成为战场环境下的重要通信手段。卫星信号调制方式识别在军事领域具有重要意义和广泛的应用前景,如干扰识别、频谱管理、通信监视、电子对抗等。目前调制方式识别的方法很多,有基于信号参数统计[1]、基于小波变换[2]、基于高阶累积量[3]等,这些方法均要求了解信号的先验信息(如精确的中心频率和调制速率),而这些先验信息在信号调制方式未知的情况下难以得到。本文针对卫星通信中常用的调制方式,提出了一种无任何先验信息条件下的卫星信号调制方式识别方法,并详细说明了方法的步骤和原理。采用此方法对卫星实测信号进行识别表明,此方法对于卫星通信中常用的调制方式如QPSK、8PSK 等具有很好的效果,具有一定的实用性和有效性。

2 信号调制方式识别原理和流程

卫星信号调制方式的识别过程必须进行数据采集、信号预处理、参数提取、特征形成、信号识别这5个步骤,如图1 所示。

图1 调制方式识别基本流程Fig.1 Basic procedures of modulation mode recognitionfor satellite signals

2.1 信号预处理

卫星信号在射频被卫星天线接收,对其下变频后进行数据采集,采集的信号为卫星对应频率的带通信号,由于信道噪声、衰落等的影响,不能直接对其进行特征提取,必须首先对信号进行预处理,目的是减小噪声、提高信号的信噪比,从而使得提取到的信号特征准确、有效。本文中,信号预处理包括信号中心频率估计与窄带滤波、去除信号直流成分。

信号中心频率估计可以在时域[6]或频域进行。时域估计适用于低频信号,要求信号具有较高的信噪比,卫星信号显然不符合该条件。在频域对信号进行中心频率估计有多种方法,文献[5]提到对信号进行四次方运算后作快速傅里叶变换得到其四次方谱,在频谱中搜索幅度最大值,对应频率的四分之一即为信号的中心频率。该方法的问题是,对信号作四次方运算后,数据处理的计算量过大,而且在四次方谱中要得到原信号中心频率4 倍处的谱线,中频信号的采样频率应至少是原信号中心频率的8 倍,这个采样频率往往过高,使该方法的应用场合受限。

本文采用的是频域估计法[7]。设

则信号的中心频率可以按照下式估计:

信号在接收端由于接收机的影响,会产生直流成分。直流成分在后面混频等处理中会产生影响,因此在提取信号参数之前应该去除信号直流成分。

令 s(t)表示信号s(t)的均值:

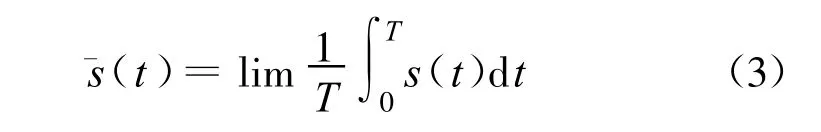
去除信号直流成分可以表示为

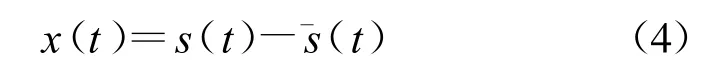
本文中,卫星下变频器输出中频信号为70 MHz,进行预处理之前,首先需要对该频段进行类似于频谱仪功能的频谱复现。对卫星下变频器输出的70 MHz、带宽36 MHz的信号进行数据采集后直接做快速傅里叶变换,得到该频段频谱图如图2 所示。

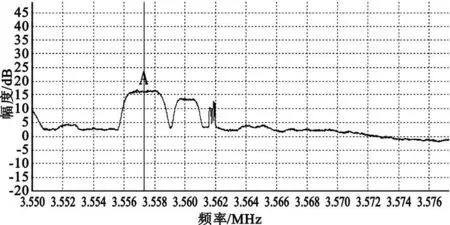
图2 通过傅里叶变换从采集数据中恢复的频谱图Fig.2 Spectrum reconstructed from samp le data by FFT

在此基础上,根据式(2)得到A 信号的中心频率为f c=3 557.318 MHz。对信号带宽的估计采用滑动窗平均法,这里采用长度为50 的滑动窗截取傅里叶变换后的频谱数据并作平均,设定门限为12 dB后,求得信号的3 dB 带宽为Bw =2.603 MHz。自适应选取通带略大于信号带宽的带通滤波器对70 MHz信号进行滤波;根据所求的信号中心频率和带宽,采用欠采样方法,控制采集卡以合适的采样频率完成数据采集。这里选择滤波器带宽为B =5.2 MHz,相应的采样时钟频率为fs=21.4 MHz。

采用欠采样方法对信号进行带通采样,采样后信号的中心频率随之改变。对采集数据做傅里叶变换恢复频谱,如图3 所示。

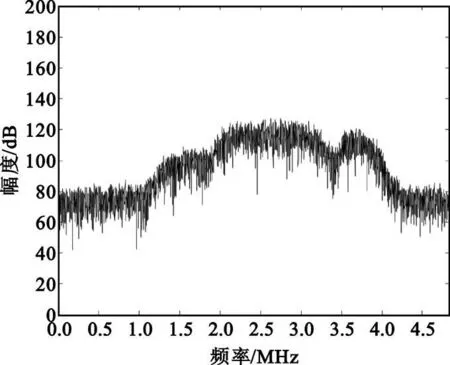
图3 带通采样后恢复的信号频谱Fig.3 Signal spectrum reconstructed after bandpass sampling

仍采用频域估计法,根据式(2)得到欠采样后信号的中心频率fc′=5.800 MHz。再根据式(4)去除信号的直流成分,这样就完成了信号预处理工作。

应当提到的是,采用频域估计法对于频谱对称的信号结果准确,而对于频谱非对称信号则会出现一定偏差,根据对卫星下行信号频谱的观测经验,多数信号为频谱对称信号,所以采用频域估计法求取信号中心频率是可行的。

信号带宽的估计值被用来设计对信号进行带通滤波时的截止频率,因此对带宽的估计值要求不高,可以适当放大带宽的估计值。

2.2 信号符号速率的提取

信号的符号速率是数字调制信号的一个非常重要的参数。准确提取信号的符号速率,才能确定后续信号处理的采样频率;如果符号速率估计错误,那么在此基础上进行码元判决得到的结果也是错误的,导致解调失败。所以,符号速率的正确提取是调制方式识别的关键环节之一。

文献[8] 将PSK 信号的瞬时相位解混叠后差分,利用相位差分序列峰值的最小间距来估计信号的符号速率。该方法适合估计低频信号的符号速率,当信号频率高于1 MHz时,估计误差大于5 kHz,不适合在本文场合使用。

文献[9]提供了利用小波变换估计MPSK 信号符号速率的方法。该方法利用小波变换多分辨率的特点在较低运算量的条件下得到准确的符号速率,不足是对于不同类型的调制方式,要求采用不同类型的母小波,也不适合在本文中运用。

延迟-相乘接收机可以估计信号的符号速率,原理是由该接收机的功率谱输出在频率fd处存在一条离散谱线,其幅度远大于附近的功率谱密度,这根谱线对应的频率值就是信号的码元速率,检测这根谱即可得到信号的符号速率。该接收机结构如图4 所示。

图4 延迟-相乘接收机结构图Fig.4 Structure of delay-multiply receiver

延迟Td取采样周期的1 000倍,得到输出的功率谱如图5 所示, 检测得到信号符号速率为Rs=2.499 MHz。利用延迟-相乘法估计信号的符号速率对于各种多种调制方式均有很好的效果,当信号信噪比较低时,可以通过增加延迟单元的长度抵消信噪比较低的不利影响,获得较准确的符号速率估计。

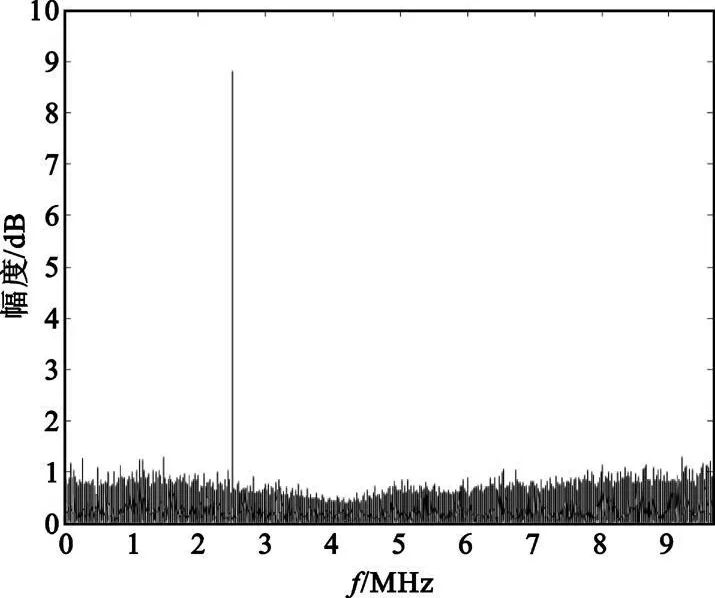
图5 延迟-相乘输出的功率谱估计Fig.5 The power spectrum estimation output by delay-multiply

2.3 特征形成与信号识别

在正确提取信号调制参数的基础上,采用相干解调法对采样信号进行解调,得到信号的I、Q 支路,利用延迟-相乘法得到的信号符号速率对采样信号进行相位恢复,即用符号速率对原序列内插,得到相位信息序列a 和b,按照信号输入方式双比特ab,得到恢复了的星座图,根据不同调制方式的星座图特征,即可判断出原卫星信号的调制方式。

3 仿真结果分析

采用本文方法对实测的卫星下行信号进行调制方式识别。卫星天线接收的C 频段射频信号经低噪声放大器后送入下变频器,下变频器输出的中频信号频率为70 MHz,带宽36 MHz。对中频信号进行预处理后,进行数据采集,按文中方法提取信号符号速率。利用此符号速率对原序列内插,得到的相位信息序列按照信号输入方式进行比特恢复,得到的星座图如图6 所示,根据图6(a)的星座图可判定该信号调制方式为QPSK,根据图6(b)的星座图可判定该信号调制方式为8PSK。

图6 不同调制方式信号恢复的星座图Fig.6 The constellation reconstructed from different signal modulation

识别不同的调制方式时,除解调方法上有所不同,前面的步骤均可通用。多次仿真结果表明,解调效果依赖于卫星下变频器输出信号的信噪比,信号的信噪比降低时,会影响信号调制方式识别的效果。利用延迟-相乘法提取的符号速率对信号相位序列内插时,由于信号信噪比的下降,使得原信号中符号“1”被误判决为符号“0”的几率增加,表现为解调后信号的误码率上升,根据相位序列恢复得到的星座图相位点出现扩散,信号信噪比降低到一定程度时,星座图相位点的扩散会使得无法识别该信号调制方式,如图7 所示。图6(a)星座图所示信号信噪比为10 dB,图6(b)星座图所示信号信噪比为12 dB,图7(a)星座图所示信号信噪比为6 dB,图7(b)星座图所示信号信噪比为5 dB。可见,当信号信噪比降低到5 dB以下时,星座图相位点的扩散使得无法正确识别调制方式。

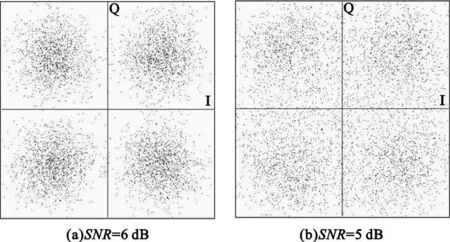
图7 不同信噪比时恢复的星座图Fig.7 Constellation in different signal′s SNR

4 结 论

本文介绍了一种在无任何先验信息条件下对卫星信号调制方式识别的新方法,详细说明了步骤和原理。该方法对实测卫星下行信号进行预处理后,通过延迟-相乘的方法检测信号符号速率,再经过内插恢复得到信号的星座图,根据不同调制方式的星座图特征对调制方式(QPSK、8PSK)加以识别,并通过实测数据验证了方法的实用性和有效性。

要得到信号的星座图,需要对信号进行解调分析。研究中发现,不同调制方式的卫星信号往往需要采用不同的解调方式,这增加了后端的复杂度,也增加了信号处理的时间。结合已提取的信号参数,进一步处理得到更多的信号特征,在对信号解调前即作出区分,将解调后的星座图作为一种验证手段,是降低信号解调复杂度的一种思路,相应的研究正在进行。

本文所提方法的特点是在无任何先验信息的情况下对卫星信号调制方式进行识别,可应用于无线电信号的监测、检测,对无线电监测、管理水平的提高具有一定意义。

[1] 杨小牛, 楼才义,徐建良.软件无线电原理与应用[M] .北京:电子工业出版社,2001.

YANG Xiao-niu, LOU Cai-yi, XU Jian -liang.Theory and App lication of Software Radio [M] .Beijing:Publishing House of Electronics Industry,2001.(in Chinese)

[2] 范海波, 杨志俊,曹志刚.卫星通信常用调制方式的自动识别[ J] .通信学报,2004,25(1):140-149.

FAN Hai-bo, YANG Zhi-jun,CAO Zhi-gang.Automatic recognition for common used modulations in satellite communication[J] .Journal on Communications, 2004, 25(1):140-149.(in Chinese)

[3] 李杨,李国通,杨根庆.通信信号数字调制方式自动识别算法研究[J] .电子与信息学报,2005,27(2):197-201.

LI Yang, LI Guo-tong, YANG Gen-qing.Automatic Digital Modulation Recognition Algorithm of Communication Signals[J] .Journal of Electronics and Information Technology,2005, 27(2):197-201.(in Chinese)

[4] 万坚, 李明,朱中梁.卫星数字调制混合信号的自动识别[ J] .电讯技术,2007,47(1):71-74.

WAN Jian, LI Ming, ZHU Zhong-liang.Automatic Modulation Recognition of Digital Mixed Signals in Satellite Communication Systems [ J] .Telecommunication Engineering,2007, 47(1):71-74.(in Chinese)

[5] 宋成森.数字通信信号调制方式识别与参数估计[ D] .杭州:浙江大学,2006.

SONG Cheng-sen.Modulation recognition and parameter estimation in digital communications[ D] .Hangzhou:Zhejiang University, 2006.(in Chinese)

[6] Hsue S Z, Soliman S S.Automatic modulation classification using zero crossing[J] .IEE Proceedings,1990(6):459-464.

[7] 宋辉.通信信号的特征分析、自动识别与参数提取[D] .南京:南京理工大学, 2003.

SONG Hui.The communication signal characteristics analysis, automatic identification and parameter extraction[ D] .Nanjing:Nanjing University of Science and Technology,2003.(in Chinese)

[8] Mammone R J, Rothaker R J.Estimation of carrier frequency, modu lation type and bit rate of an unknown modu lated signal[ J] .IEEE Communications,1987, 28(4):1-7.

[9] Chan Y T, Plews J W,Ho K C.Symbol rate estimate by thewavelet transform[ C]//Proceedings of 1997 IEEE International Symposium on Circuit and System.Hong Kong:IEEE,1997:177-180.