连体位置及刚度变化对双塔楼地震响应的影响
2012-03-15盛宏玉
汪 莉, 盛宏玉
(合肥工业大学土木与水利工程学院,安徽合肥 230009)
双塔楼连体建筑有利于防火,由于连体结构的存在多了疏散通道,一旦发生火灾人们可以通过连体通道转移到安全地带,减少了人员伤亡。连体通道的设置方便了人们的交流,两栋楼里的人们通过连体可以便捷地互通,从而节约了大量的宝贵时间。还可以在连体上设置休闲地带,使人们在工作疲劳之时能得到更好的休息和调整。
连接体的存在使得原来彼此独立的单体变成了连体结构,结构的动力特性和抗震性能发生了很大变化。对于双塔楼连体结构的动力特性和抗震性能,已有很多研究成果:文献[1]以一实际高层建筑连体结构为背景,采用弹塑性动力时程分析方法对其进行抗震分析,探讨高层建筑连体结构在罕遇地震作用下的动力响应,重点讨论了在罕遇地震下结构的侧移、内力及塑性铰的发展变化;文献[2]结合我国南方某连体大厦的施工方案,主要介绍了连体结构的形式,并对这个连体结构的施工工艺进行了详细的阐述和探讨;文献[3]以绍兴环球纽约国际中心工程为例,对结构进行了多遇地震下弹性计算分析、时程分析、中震不屈服分析,为结构技术设计和采取有效抗震加强措施提供了依据;文献[4]结合一非对称高层连体结构,研究在多点输入下的地震响应;文献[5]分析了连体结构在竖向地震作用下的响应。但是关于连体刚度及位置变化对结构地震响应的影响的研究还不是很多。本文采用有限元分析软件SAP2000对某对称双塔楼连体结构进行动力时程分析,通过计算分析和结果比较进一步了解连体位置及刚度变化对结构的抗震影响。
1 建立有限元模型
模态分析是用来确定结构振动特性的方法,它是结构动力分析的一个重要方面。结构的振动特性主要包括固有频率、振型等,求解的是经典的特征值问题,可表示为:

其中,ωi、φi、K、M分别为第i阶模态的圆频率、振型向量、刚度矩阵和质量矩阵。通过模态叠加原理可以求解结构的线性动力响应。
通常情况下采用时程分析法求解结构的动力响应[6]。在地震作用下,多自由度弹性体系的振动微分方程为:
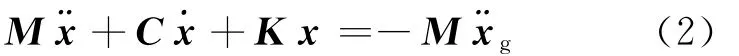
其中,C为体系的阻尼矩阵;¨x为质点的加速度矢量;˙x为质点的速度矢量;x为质点的位移;¨xg为地面加速度矢量。
时程分析法就是根据选定的地震波和结构恢复力特性曲线,在每一个很短的时间间隔Δt内,利用数值积分的手段求解方程(2)的方法。本文所用的SAP2000程序采用的是HHT法[7],H HT法本质上是Newmark方法的发展,它引入α参数并修改结构动力方程,如(3)式所示,使用Newmark方法进行求解。
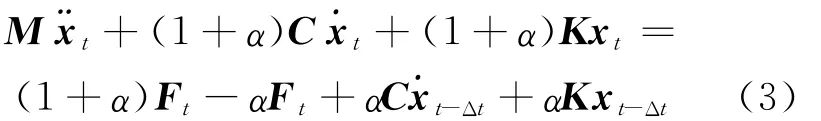
本文算例为15层钢筋混凝土框架结构,采用有限元软件SAP2000对其进行离散化,结构的空间模型如图1所示。其横纵方向柱距均为6 m,连廊跨度为9 m,层高均为3 m,角柱截面为600 mm×600 mm,中柱截面500 mm×500 mm,边梁截面为300 mm×500 mm,框架梁截面为250 mm×500 mm,次梁截面为200 mm× 500 mm,连体梁截面为400 mm×700 mm,板厚取100 mm,混凝土强度等级采用C30,钢筋采用HRB335级。建筑类别为乙类建筑,设防烈度为7度,场地为Ⅱ类场地,设计地震分组为第1组,特征周期为0.35 s,地面粗糙度为B类,基本风压为0.4 k N/m2,结构阻尼比为0.05[8]。在地震响应分析时考虑了基本风压的影响,并将其视为常量。本文选取一条适合于Ⅱ类场地的El-Centro波,峰值加速度为341.7 cm/s2,从2个塔楼并列的方向(X方向)输入地震波。El-Centro波的加速度时程曲线如图2所示。

图1 结构有限元模型图
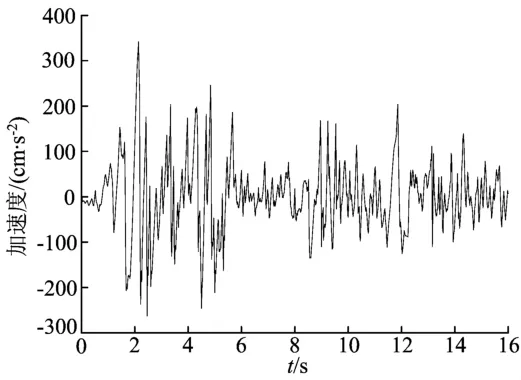
图2 El-Centro波加速度时程曲线
算例1 按照图1所示模型,连廊位于14~15层,其刚度为基本刚度,计算参数按结构原型的设计资料选取。
算例2 改变连廊位置,将其设在9~10层,连廊刚度为基本刚度,其余参数按照算例1选取。
算例3 改变连廊位置,将其设在4~5层,连廊刚度为基本刚度,其余参数按照算例1选取。
算例4 保持连廊位置不变(位于14~15层)改变连廊刚度,连体梁截面取为500 mm× 1 000 mm,其余参数按照算例1选取。
算例5 保持连廊位置不变(位于14~15层)改变连廊刚度,连体梁截面取为600 mm× 1 500 mm,其余参数按照算例1选取。
2 算例分析
根据SAP2000中模态分析的结果,分别提取不同算例前12阶自振周期并作对比,见表1所列。
由表1可知:除了算例3,其余算例在第4阶振型时振动周期迅速减小,越往高阶振动周期减小越缓慢。随着连廊位置的降低,结构的自振周期逐渐变小,结构趋刚。随着连廊刚度的增大,结构的低阶自振周期逐渐变大,但变化幅度不大,可能是因为连体梁刚度变化不大。
在El-Centro波的作用下,结构发生了一定的地震响应。不同算例的X向顶点位移时程变化如图3所示,结构的X向基底剪力如图4所示。
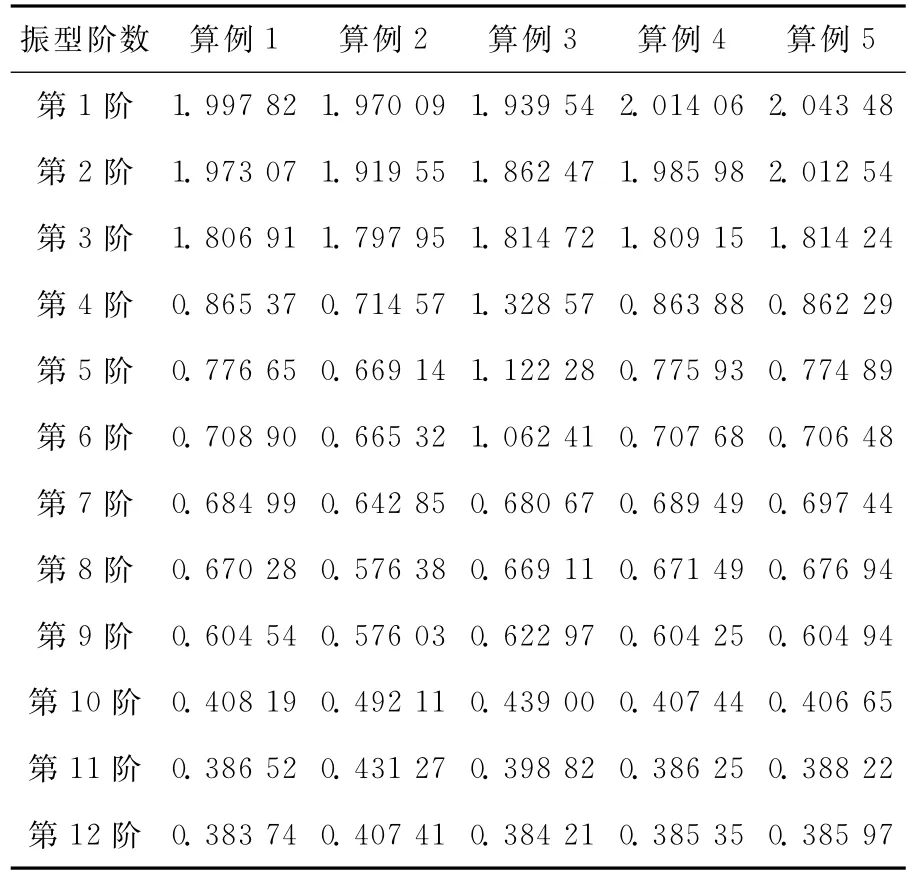
表1 不同算例结构的自振周期对比 s
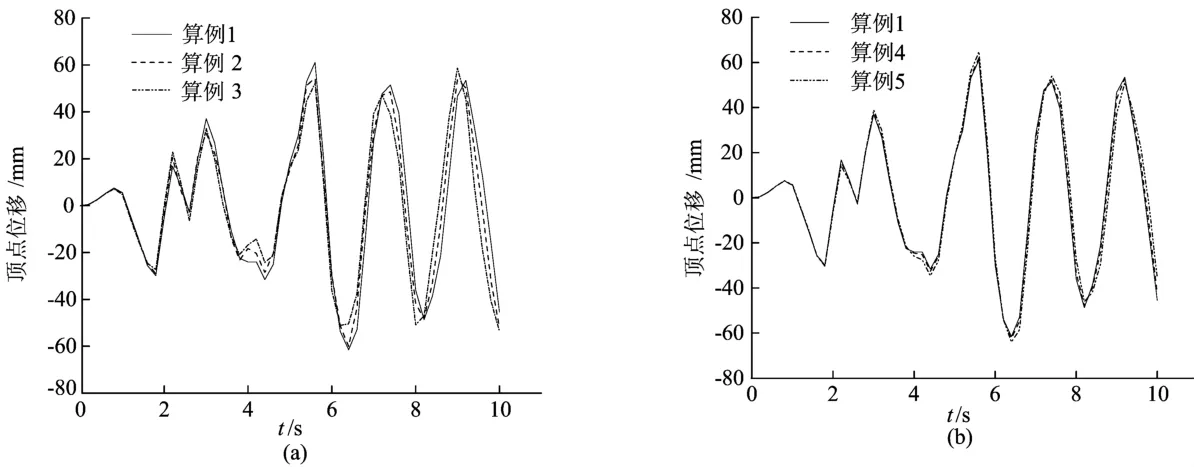
图3 顶点位移时程曲线
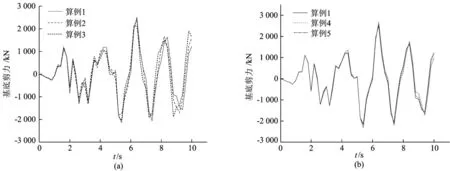
图4 基底剪力时程曲线
为了清晰地将不同算例结构的地震响应进行对比,表2列出了各算例顶点位移的最小值和最大值,表3列出了各算例基底剪力的最小值和最大值。
由表2可知:X方向顶点位移最小的是算例3,X方向顶点位移最大的是算例5,Y方向顶点位移最小的是算例2,Y方向顶点位移最大的是算例5。Y方向的顶点位移比X方向的位移小很多。随着连廊位置的变化,顶点位移逐渐减小,X方向最大顶点位移减小幅度最大为10.9%;随着连廊刚度的变化,顶点位移逐渐增大,X方向顶点位移增大幅度最大为6.0%。
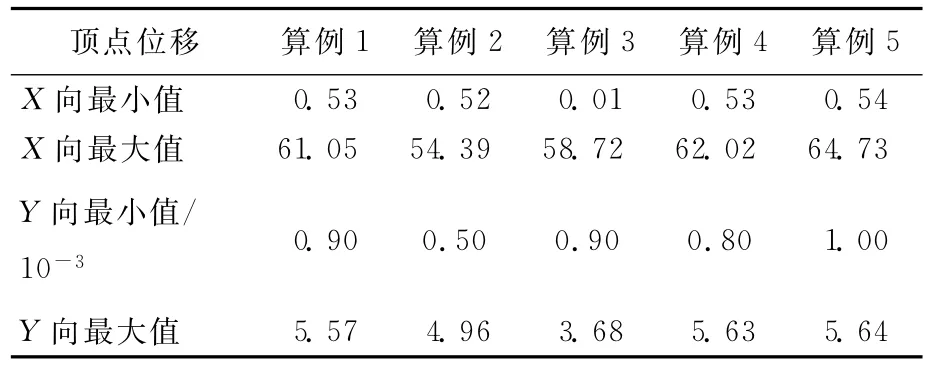
表2 不同算例结构的顶点位移对比 mm
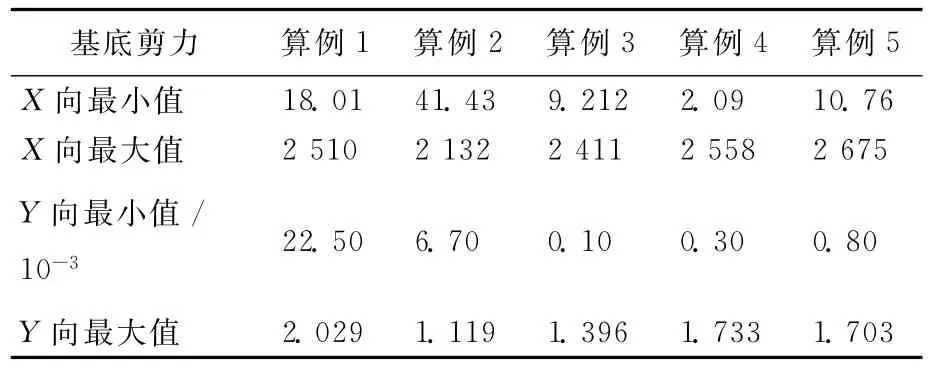
表3 不同算例结构的基底剪力对比 k N
由表3可知:X方向基底剪力最小的是算例4,X方向基底剪力最大的是算例5,Y方向基底剪力最小的是算例3,Y方向基底剪力最大的是算例1。Y方向的基底剪力比X 方向的基底剪力小很多。随着连廊位置的变化,X方向最大基底剪力在减小,减小幅度最大为15.1%,随着连廊刚度的变化,X方向最大基底剪力在增大,增大幅度最大为6.6%。
本文在分析地震响应的同时考虑了风荷载作用,并与不考虑风荷载作用的情况做了对比。算例1与不考虑风荷载作用时顶点X向加速度对比如图5所示。
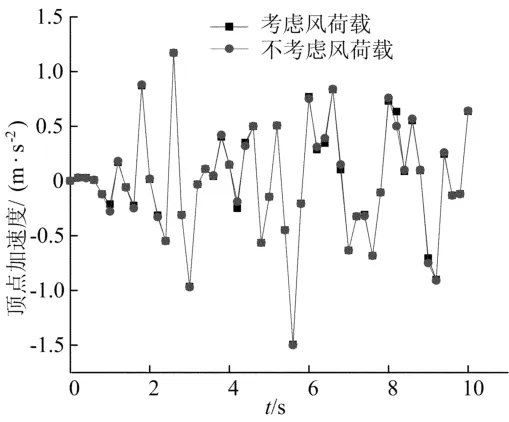
图5 顶点X向加速度时程曲线
3 结 论
(1)等高对称的双塔楼连体结构前3阶自振周期很接近,数值降低变化不大;从第7阶后自振周期变化趋于平稳;由于连廊的位置和刚度对高阶的自振周期影响不大,设计时可主要考虑对前几阶周期的影响。
(2)随着连体位置的下降,顶点的最大位移逐渐减小,连廊位于9~10层的算例最小;结构基底剪力最大值逐渐增大,连廊位于9~10层的算例最小。随着连体刚度的变化,顶点的最大位移、最大基底剪力都在增大。Y方向顶点位移、基底剪力很小,对研究结构的地震响应影响不大,可以不予考虑。
(3)以顶点位移为控制指标时,算例2最为合理;以基底剪力为控制指标时,算例2最为合理。
(4)在地震响应分析时考虑风荷载与不考虑风荷载2种情况下,顶点X向加速度时程变化曲线基本相同。风荷载对结构地震响应的影响很小,设计时可以忽略不计。
[1] 李海旺,梅志强.某高层建筑连体结构的抗震分析[J].山西建筑,2008,34(1):5-6.
[2] 霍建利.高层建筑连体结构施工技术的应用[J].科技创新导报,2009(7):24.
[3] 恽 波,乐建新,裘 涛.双塔楼高层建筑结构设计[J].浙江建筑,2010(4):11-14.
[4] 安东亚.非对称超高层连体结构多点输入地震响应研究[J].防灾减灾工程学报,2010,30(Z1):82-88.
[5] 张 力,石洪林,李世超.连体结构在竖向地震作用下的分析[J].低温建筑技术,2006(6):73-75.
[6] 淦克丽,盛宏玉,叶献国.巨型框架减振结构的动力时程分析[J].合肥工业大学学报:自然科学版,2010,33(1):81-84.
[7] 北京金土木软件技术有限公司,中国建筑标准设计研究院. SAP2000中文版使用指南[M].北京:人民交通出版社,2006:306-324.
[8] GB 50011-2001,建筑抗震设计规范[S].
