模糊线性微分系统的近似解析解

王 磊

（1.辽宁工程技术大学基础教学部，辽宁葫芦岛 125105；2.辽宁工程技术大学理学院，辽宁阜新 123000）

由于在社会科学以及工程领域的运动问题研究中模糊性的大量存在，模糊微分方程的研究越来越受到关注［1－5］。而模糊线性微分系统（模糊微分方程组）的研究则是近几年被提出的［6］；文献［7］利用λ－水平截集研究模糊线性微分系统初值问题；文献［8］从测度论的角度研究了一阶模糊线性微分系统解的结构；文献［9－10］将λ－水平截集表示成复数，从而把模糊线性微分系统转化成经典的常微分线性系统，分别研究了模糊初值和系数矩阵为模糊矩阵2种情形下系统的解；文献［11］利用一种新的扩展原理研究了一阶微分方程组模糊初值问题；文献［12］利用特征值和特征向量法研究了由结构元法线性生成的模糊线性微分系统的解析解。

以上方法都是求模糊微分系统的解析解，然而由微分方程理论可知只有少数的微分系统才有解析解，所以有必要研究模糊微分系统的近似解析解。因此，本文利用结构元方法将模糊微分系统转化成分明的线性微分系统，进而利用变分迭代法［13－14］给出方程的近似解析解。

1 预备知识

定义1 设E为实数域R上的模糊集，若隶属函数E（z），z∈R满足：①E（0）＝1；②在区间［－1，0）上E（z）是单增右连续函数，在区间（0，1］上是单降左连续函数；③ 当－∞＜z＜－1或 1＜z＜＋∞时，E（z）＝0，且E（－z）＝E（z），称E为R上的对称模糊结构元［15］。

定理1 设E是R上的任意模糊结构元，又设函数f（t）在区间［－1，1］上是单调有界的，＾f（t）是f（t）的延拓集值函数，则＾f（E）是R上有界闭模糊数，且＾f（E）的隶属函数为E（f－1（t）），这里f－1（t）是f（t）关于变量t和y的轮换对称函数（若f（t）是连续严格单调的，则f－1（t）是f（t）的反函数）［15］。

定义2 设二元函数g（t，y）＝f（t）＋ω（t）y，其中f（t）和ω（t）在T⊆R上有界，且ω（t）非负，易知函数g（t，y）关于y在［－1，1］上单调有界，对于给定的对称结构元E，称（1）式为模糊结构元E线性生成的关于变量t的模糊值函数［15］，即

对于给定t∈T，f（t）和ω（t）≥0都为常数，则（1）式为由模糊结构元E线性生成的模糊数。

定理2 设模糊值函数~x（t）由对称模糊结构元E线性生成，即~x（t）＝f（t）＋ω（t）E，且ω（t）非负，若函数f（t）和ω（t）可导［15］，则

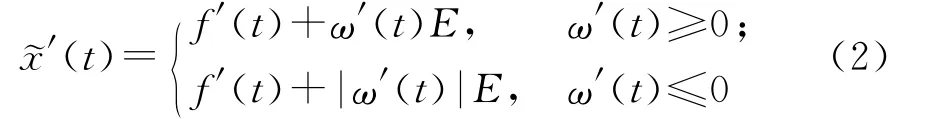
定理2表明，对于模糊结构元E线性生成的模糊值函数~x（t），其导函数也是由结构元E线性生成的模糊值函数。

2 模糊线性微分系统的变分迭代法

2.1 线性生成的模糊线性微分系统

线性微分系统：

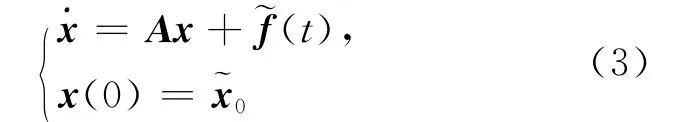
其中，A＝（aij）n×n∈Rn×n；），…，。

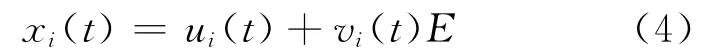
其中，ui（t）、vi（t）为未知函数，且vi（t）≥0，有

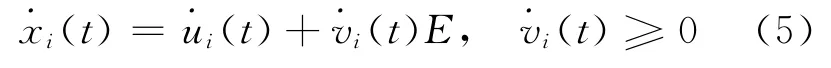
将方程（4）、（5）带入系统（3），得2个分明的线性微分系统：

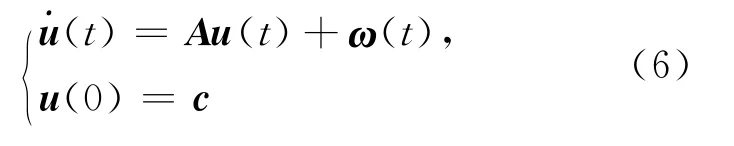
和

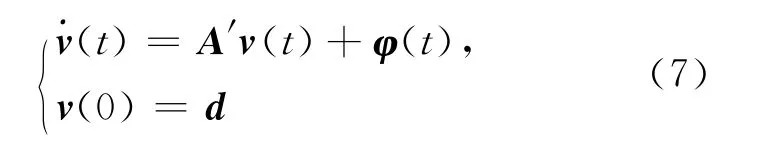
其中，c＝（c1，c2，…，cn）T；d＝（d1，d2，…，dn）T；A′＝（a′ij）n×n（i，j＝1，2，…，n）；ω（t）＝（ω1（t），ω2（t），…，ωn（t））T；φ（t）＝（φ1（t），φ2（t），…，φn（t））T，且

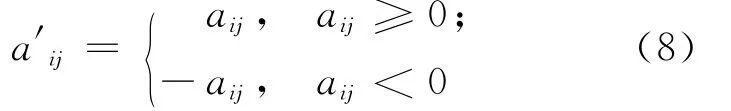
于是，系统（3）的求解便转化为对分明的线性微分系统（6）和（7）的求解，文献［12］利用特征值和特征向量法［9］给出了系统（6）和（7）的解。然而，大多数微分方程往往很难或不可能获得其解析解，有时即使能求出解析解，也因表达式过于复杂而不实用，因此下面利用变分迭代法给出系统（6）和（7）的近似解析解。

2.2 分明线性微分系统的变分迭代法

为了说明变分迭代算法［13－15］的基本思想，考虑如下的非线性方程：

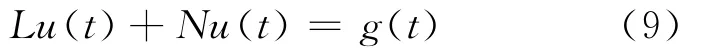
其中，L为线性算子；N为非线性算子；g（t）为已知的连续函数。利用变分迭代算法的思想为（9）式构造一个校正泛函如下：

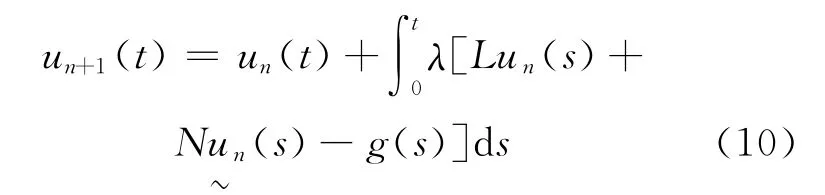
其中，λ为广义拉氏乘子，可用变分理论最佳识别；un（t）为初始近似解（可以包含待定常数或待定函数）为限制变分量，即＝0。

下面给出如下的一阶分明线性微分系统的变分迭代算法：

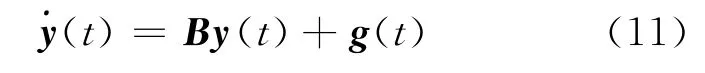
其中，y（t）＝（y1（t），y2（t），…，yn（t））T；g（t）＝（g1（t），g2（t），…，gn（t））T；B＝（bij）n×n∈Rn×n。考虑系统（11）的第i个方程：

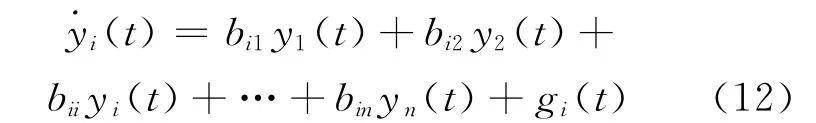
构造校正泛函如下：

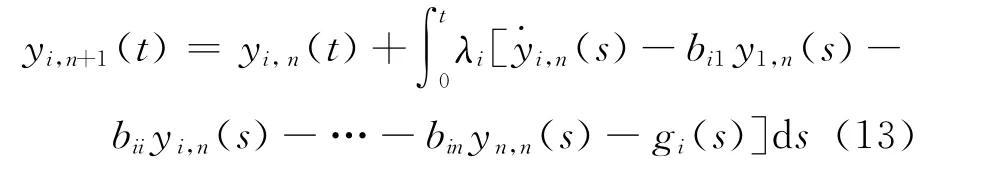
其中，yi，n（t）表示第i个方程的第n次近似解。令上述校正泛函取驻值，有

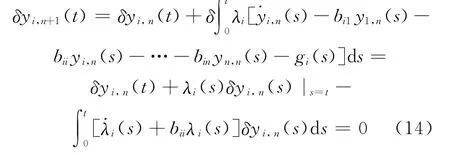
于是，得驻值条件：

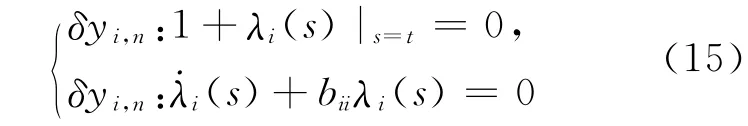
由常微分方程理论，广义拉氏乘子λi可识别为：

于是系统（11）的第i个方程的近似解表示为：

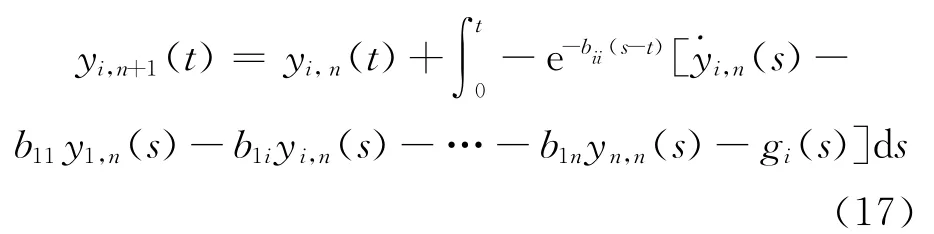
令i＝1，2，…，n，得系统（11）近似解的变分迭代算法的矩阵为：

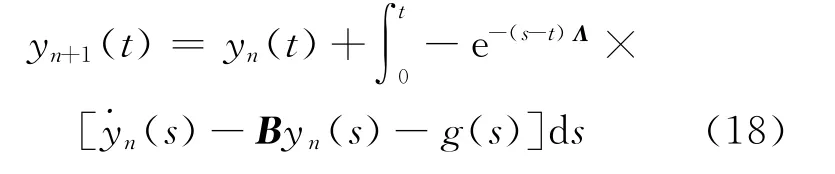
其中，Λ＝diag［b11，b22，…，bnn］。

于是，根据算法（18）求得系统（6）和（7）的近似解，进而求得原模糊系统（3）的模糊近似解。

3 算 例

例1 考查如下的模糊线性微分系统：

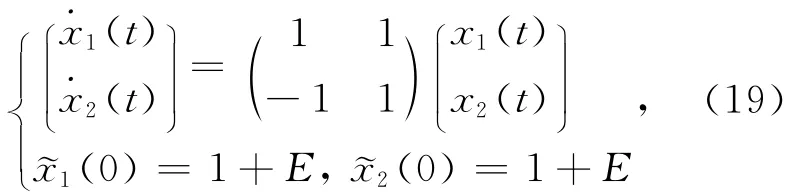
其中，E为三角模糊结构元。

解 根据前面讨论，系统（19）可转化为：

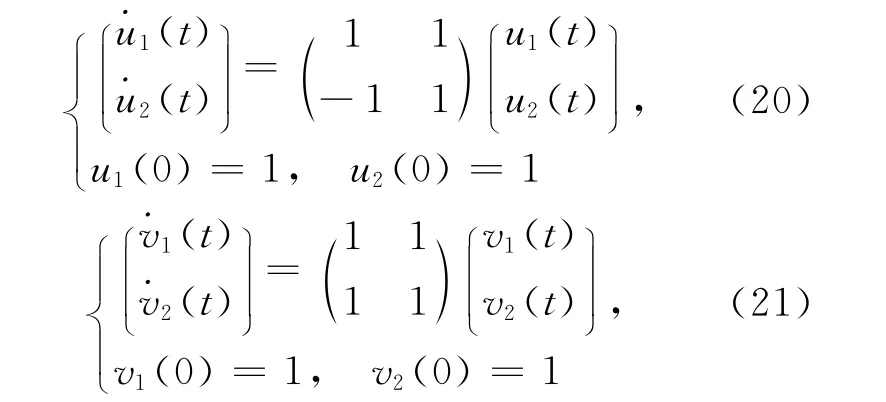
利用特征值和特征向量法［9］得系统（20）和（21）的解析解为：

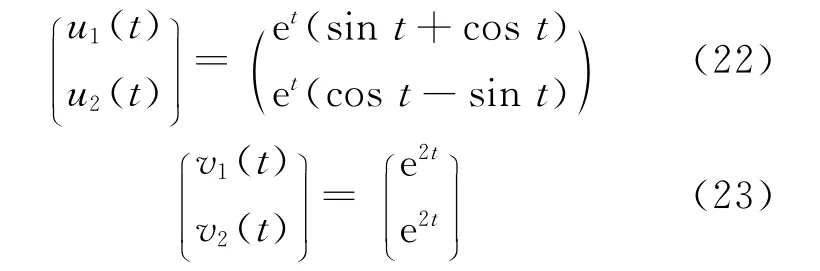
于是系统（19）的模糊解为：

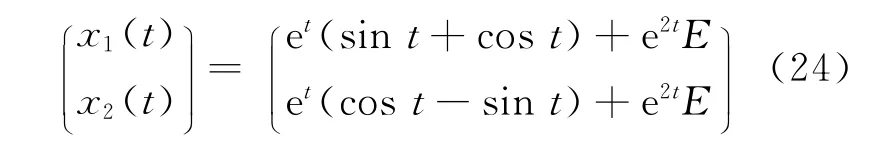
根据（18）式的变分迭代算法，进行6次迭代计算得系统（20）和（21）的近似解为（25）式、（26）式。其中分别表示u1（t）、u2（t）、v1（t）、v2（t）的近似值。

于是系统（19）的模糊近似解为（17）式。

取t∈［0，1］，近似解与精确解的误差见表1所列。其中，u1（t）与（t）的误差采用的计算公式为，其余类似。表1中的误差反映出逼近效果较好。

表1 近似解与精确解的误差

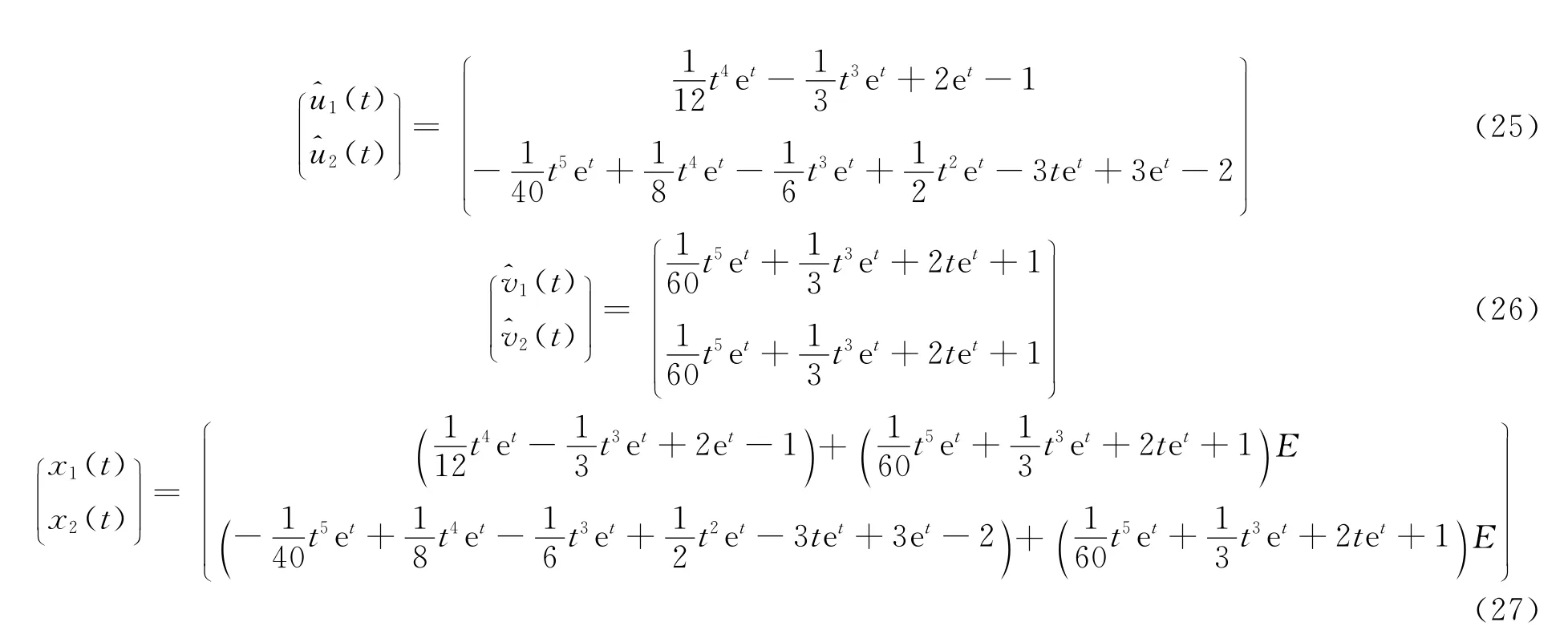
将t∈［0，1］进行10等分，图1a给出了近似解＾u1（t）、＾u2（t）和精确解u1（t）、u2（t）的比较，图1b给出了＾v1（t）、＾v2（t）和v1（t）、v2（t）的比较，反映出逼近效果较好，说明了变分迭代法的有效性。

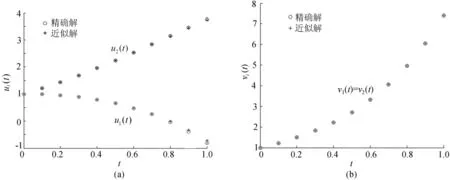
图1 例1近似解与精确解比较

例2 考察下面的捕食者－猎物模型［13］：

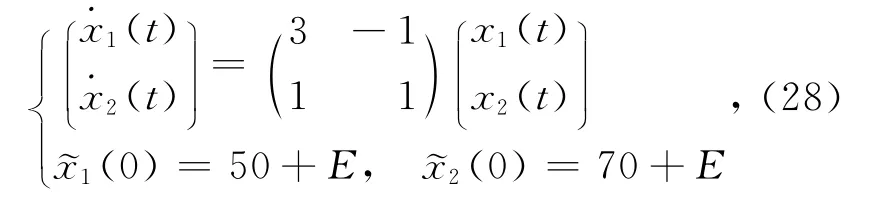
其中，E为三角模糊结构元。

解 利用特征值和特征向量法［9］得解析解：

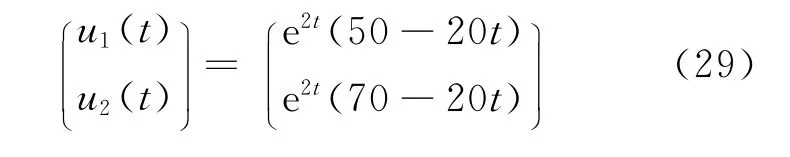
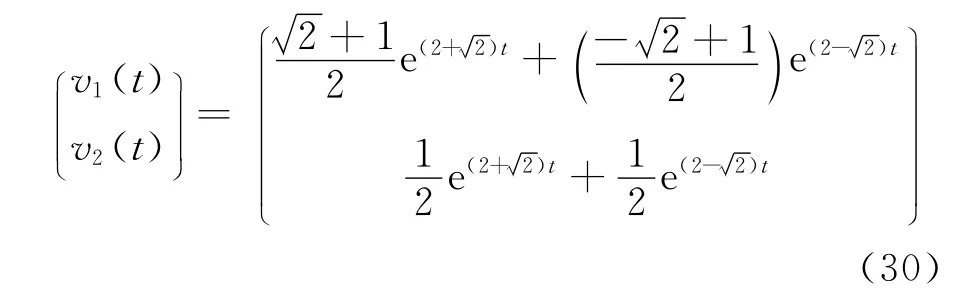
由（18）式的变分迭代算法，进行6次迭代计算得近似解为（31）式、（32）式。将t∈［0，1］进行10等分，图2给出了近似解和精确解的比较，进一步说明了变分迭代法的有效性。

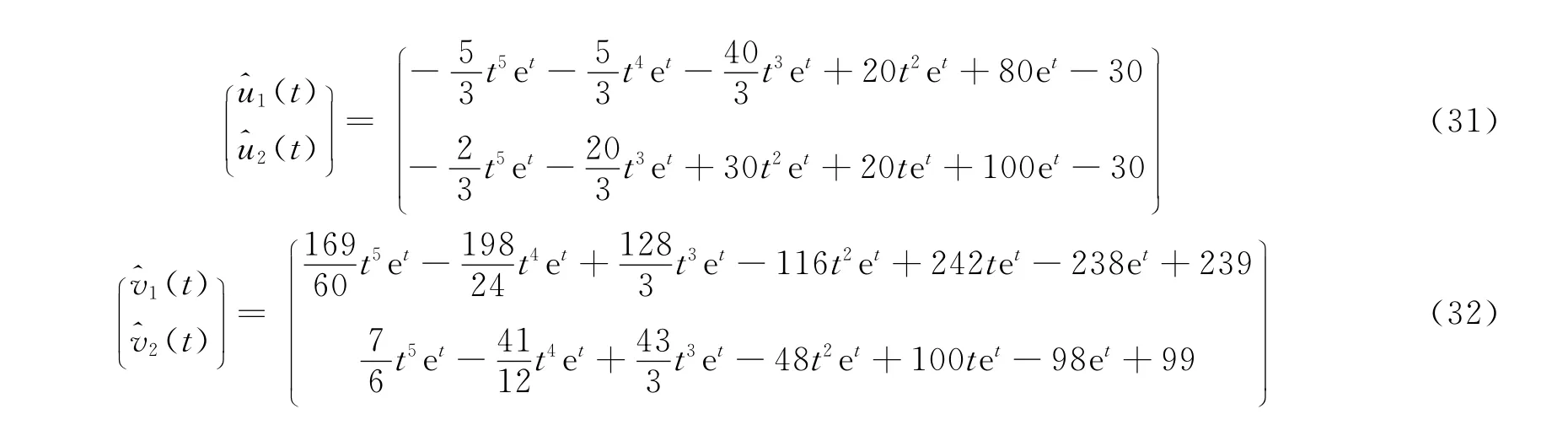
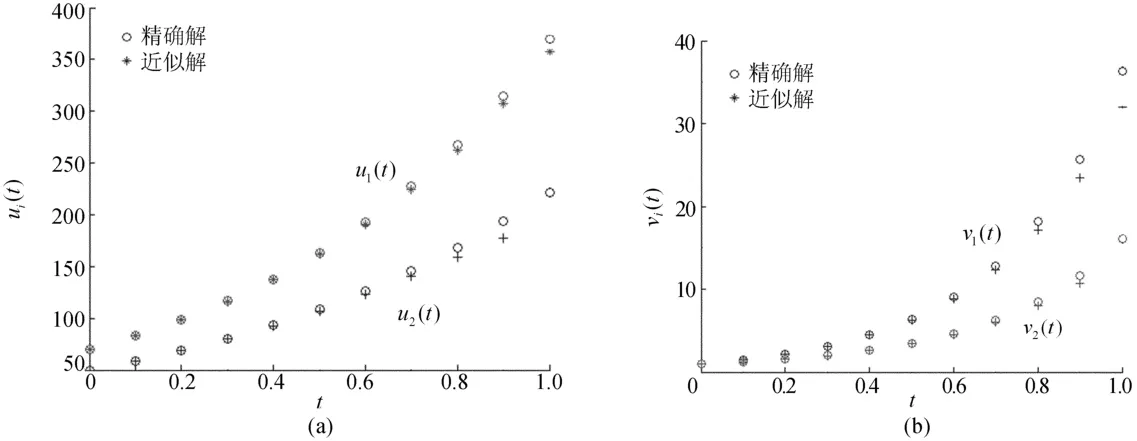
图2 例2近似解与精确解比较

4 结束语

本文利用结构元方法将模糊线性微分系统的模糊初值问题转化成同解的分明线性微分系统的值问题，构造了求解分明线性微分系统的变分迭代法，给出了模糊线性微分系统的模糊近似解。实际计算中可根据逼近精度需要选择迭代次数。

［1］ Wu C X，Song S J.Existence and uniqueness of solutions to the Cauchy problem of fuzzy differential equations［J］. Fuzzy Sets and Systems，2000，110：55－67.

［2］ Bede B，Rudas I J，Bencsik A L.First order linear fuzzy differential equations under generalized differentiability［J］. Information Sciences，2007，177（7）：1648－1662.

［3］ Misukoshi M，Chalco－Cano Y，Rom＇an－Flores H，et al. Fuzzy differential equations and the extension principle［J］. Information Sciences，2007，177：3627－3635.

［4］ 王 磊，郭嗣琮.一阶线性模糊微分方程的解［J］.模糊系统与数学，2011，25（3）：113－118.

［5］ 王 磊，郭嗣琮.一阶线性模糊微分方程的模糊结构元解法［J］.合肥工业大学学报：自然科学版，2011，34（10）：1576－1579.

［6］ Seikkala S，Vorobiev D.Towards the theory of fuzzy differential equations［J］.Fuzzy Sets and Systems，2002，125：231－237.

［7］ Buckley J J，Feuring T，Hayashi Y.Linear system of first order ordinary differential equations：fuzzy initial equation［J］.Soft Computing，2002，6：415－421.

［8］ Nieto J J，Rodrguez－Lpez R，Georgioud D N.Fuzzy differential systems under generalized metric space approach［J］. Dynamic Systems and Applications，2008，17：1－24.

［9］ Xu J P，Liao Z G，Hu Z N.A class of linear differential dynamical systems with fuzzy initial condition［J］.Fuzzy Sets and Systems，2007，157：2339－2358.

［10］ Xu J P，Liao Z G，Nieto J J.A class of linear differential dynamical systems with fuzzy matrices［J］.Journal of Mathematical Analysis and Applications，2010，368：54－68.

［11］ 王 磊，郭嗣琮.一阶线性模糊微分方程组的模糊初值问题［J］.辽宁工程技术大学学报，2010，29（5）：749－751.

［12］ 王 磊，郭嗣琮.线性生成的完全模糊线性微分系统［J］.系统工程理论与实践，2012，32（2）：341－348.

［13］ 何吉欢.变分迭代算法：一种新的非线性分析方法［J］.上海力学，1998，19（3）：260－264.

［14］ He J H，Wu X H.Variational iteration method：New development and applications［J］.Computers and Mathematics with Applications，2007，54：881－894.

［15］ 郭嗣琮，苏志雄，王 磊.模糊分析计算中的结构元方法［J］.模糊系统与数学，2004，18（4）：68－75.