基于判别分析的高速公路交通安全实时评价指标

徐铖铖 刘 攀 王 炜 蒋 璇

(东南大学交通学院，南京210096)

交通事故是道路环境特征、交通流特征、驾驶员行为与车辆特性共同作用的结果.由于难以定义在某种道路特征或交通流特征下交通事故一定会发生，因而交通安全中利用风险来描述发生事故的不确定性.传统交通安全中利用事故频次或者事故率来量化事故风险，并通过交通事故预测模型建立事故频次(或事故率)与某一较长时间段内(通常为1年)交通参数平均值(如年平均日交通量等)、交通设施特征(如车道数等)、环境条件(如路面状况等)等因素之间的关系［1-7］.这些模型通过预测一条道路或某些路段在未来一段时间内的期望事故频次(或事故率)来量化事故风险，因而可以用来鉴别事故黑点、评价交通流变化和各种交通设施对于降低事故风险的作用.

由于以往事故预测模型采用较长时间段交通流参数的平均值进行建模，无法反映交通流短时间变化对事故风险的影响，因而难以对道路交通安全状况进行实时评价.随着动态交通控制系统(如高速公路可变限速控制系统、高速公路匝道控制系统等)在高速公路上的不断应用，海量高精度实时交通流数据的获取不再困难.已有研究表明高速公路交通事故风险与交通流运行中某些实时状态参数(如速度差、交通密度和上下游断面速度差等)之间存在显著关系［8-16］.因而为了实时评价交通流变化对高速公路事故风险的影响，本文采用高精度交通流数据建立高速公路交通安全实时评价指标，用以实时评价高速公路交通安全状况和预测交通事故的发生.

1 数据来源与特征

由于国内高速公路交通流检测设备的布设密度相对较低，交通流数据的采集精度相对较低，以及历史交通流数据保存不完整等原因，本文提取了美国加州I-880 N 高速公路上的实时交通流和交通事故数据.研究路段长约35 km，单向共有47 组交通流线圈检测器，各个线圈之间距离的平均值约为0.8 km.提取了I-880 N 研究路段从2010年1—12月的交通事故和实时交通流数据，这些数据中共包含509 起交通事故.

I-880 N 研究路段上交通流线圈检测器采集的数据包括速度、流量和占有率3 个参数.原始交通流数据的采集间隔为30 s，本文采用5 min 汇集间隔对原始交通流数据进行处理，计算各个交通流参数的平均值和标准差，在已有研究中也通常采用5 min 作为汇集间隔［8-10］.交警部门记录的交通事故发生时间往往晚于实际的交通事故发生时间，因而这里需要根据交通流参数的变化来估计交通事故的实际发生时间［8-10］.交通事故的发生会造成上游车辆的突然减速并形成拥堵，因而通过观察事故发生前一段时间上游线圈速度和占有率的变化，可以对交通事故发生时间进行校准.如图1所示，460号交通事故记录的发生时间为7:56，上游线圈的速度和占有率在7:50 开始出现连续性突变，因而将460 号交通事故发生时间校准为7:50.本文研究实时交通流参数对交通事故的影响，因而只提取了6:30—18:30 这段时间的交通事故.已有研究表明从夜里到清晨这段时间道路流量很小，交通事故主要是由驾驶员的不合理驾驶行为而不是危险交通流特征造成的［10］.

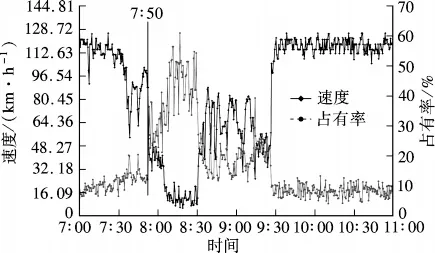
图1 事故发生时间校准

采用配对病例-对照方法提取研究数据，其中病例为交通事故发生前的交通流特征，对照为没有发生事故条件下的交通流特征.对照和病例的比例采用了最常用的4∶1 比例［16］，对照组数据的选取考虑了如下条件:①对照组所在日期与对应事故所在日期不同;②与事故发生时间对应;③与事故发生地点对应;④对照组当日在该点处没有发生交通事故.提取了2 组相邻线圈的交通流数据，这2 组线圈分别在事故发生地点的上游和下游(见图2).

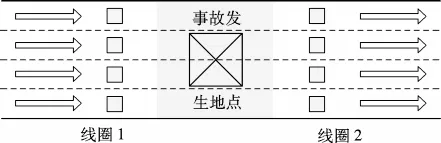
图2 研究所需线圈示意图

本文提取了事故发生前5 min 的交通流数据，同时对应于每起事故还提取了4 组没有发生事故条件下的交通流数据.例如989 号事故发生在桩号26.84 处，发生时间为2010年7月20日13:15.提取2010年7月20日13:10—13:15 事故发生地点上下游2 组线圈的交通流数据(见图2)作为一个病例，并在该处随机选取4 d 从13:10—13:15 的交通流数据作为4 个对照，并且这4 d 在该处都没有交通事故发生.事故组(病例组)共包含509 个样本，而非事故组(对照组)共包含2 036 个样本.按4∶1 的比例将数据随机分成训练样本和验证样本.其中训练样本包含407 个事故数据和1 628 个非事故数据，验证样本包含102 个事故数据和408个非事故数据.

2 数学模型

2.1 Fisher 判别分析

利用Fisher 判别分析方法建立实时交通流参数的线性组合，以判别可能导致交通事故发生的危险交通流状态.Fisher 判别分析的基本原理为将原来在高维空间各个类别的自变量组合投影到低维空间，从而使各个类别在低维空间的重合最小［17］.图3以一个二元分类问题为例说明Fisher 判别分析的基本原理，2 个类别的自变量组合被投影到坐标轴D1和坐标轴D2上，可以看出坐标轴D2上类别A 和类别B 的重合区域要远小于坐标轴D1上类别A 和类别B 的重合区域.因此，D2的判别性能要高于D1.Fisher 判别分析的目的是找到重合区域最小的低维投影空间.

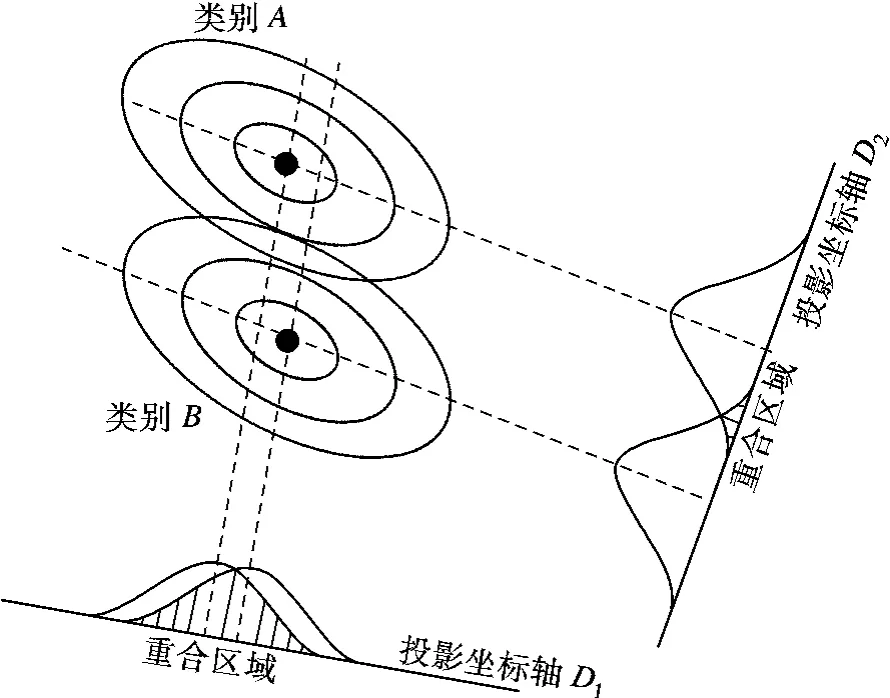
图3 Fisher 判别分析基本原理示意图［17］

Fisher 判别分析能够将一个高维问题(维数为自变量数)转换为小于等于G－1 维的低维问题，其中G 为结果变量选择项的数目.由于本文研究的结果变量只涉及2 个选择项，即可能引起交通事故的危险交通流特征和正常条件下的安全交通流特征，因此这里只需要一个判别函数.该判别函数为显著影响交通事故风险的实时交通流参数的线性组合，其表达式如下:

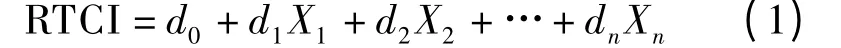
式中，RTCI 为高速公路交通安全实时评价指标;d0为判别函数的常数项;d1，d2，…，dn为判别函数各个解释变量的系数;X1，X2，…，Xn为解释变量.该判别函数能够将与交通事故相关的实时交通流参数转变为一个判别函数值，本文将该判别函数值定义为高速公路交通安全实时评价指标，用来实时评价高速公路交通安全状况和预测交通事故的发生.

2.2 条件logistic 回归

条件logistic 回归模型常用于分析基于配对病例-对照方法提取的研究数据［8，16］，该模型可以消除混杂因素对研究结果的影响.如前所述，本文在数据处理过程中将4 组非事故数据与1 组事故数据进行配对，因而可以采用条件logistic 回归模型来分析事故组和非事故组对应的RTCI 值.由条件logistic 回归模型估计的比值比可用来量化RTCI值对交通事故风险的影响，即每单位RTCI 值的变化对交通事故风险的影响.结果变量Y 为二元变量，即Y=1 代表事故发生，Y =0 代表没有事故发生.对于第j 个配对组，解释变量x1，x2，…，xp对应的交通事故发生条件概率P 为［8］

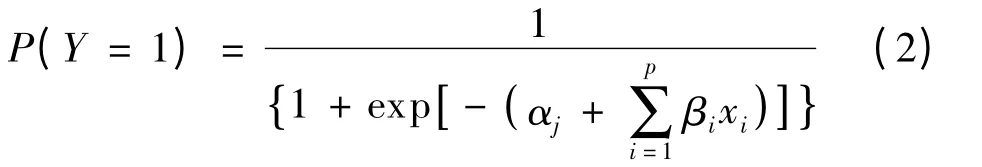
式中，αj为各个配对组的常数项，在条件logistic 回归模型中αj不参与估计;xi为解释变量，即RTCI;βi为解释变量，即RTCI 对应的系数.

用来估计解释变量系数βi的条件似然函数表达式为

式中，N 为配对的组数;c 为每个配对组中对照的数量;xj0i，xjki分别为第j 个配对组中病例样本和第k 个对照样本的解释变量xi值.

3 结果与讨论

3.1 模型建立

已有研究表明许多交通流参数与交通事故风险都存在显著关系［8－16］，这些变量用来作为Fisher判别分析的备选变量.本文采用如下步骤选择用于建立高速公路交通安全实时评价指标的变量:

①计算各个备选变量之间的相关系数，建立多组备选变量组合，其中各组中包含尽可能多不相关的变量.

②对各组备选变量组合执行Fisher 判别分析，产生各个组合对应的判别函数，剔除不显著的判别函数.

③检验各个判别函数中每个解释变量的判别能力，剔除不显著的解释变量.

④对比分析各个判别函数的判别精度，选取判别精度最高的判别函数建立高速公路交通安全实时评价指标.

模型利用统计分析软件SPSS 的判别分析模块进行估计［17］.其中，判别精度最高的判别函数包含6 个解释变量，表达式如下:

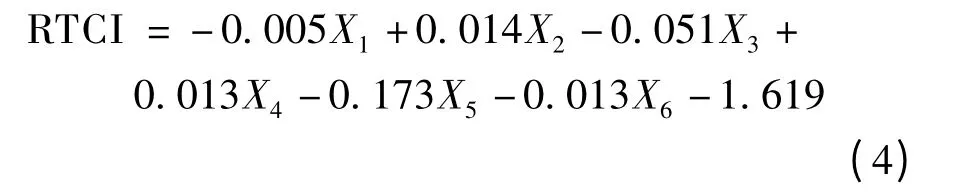
式中，X1为上游线圈交通流量在5 min 内的平均值，辆/(30 s·车道);X2为上游线圈的平均速度，km/h;X3为上游线圈的速度标准差，km/h;X4为下游线圈的平均速度，km/h;X5为下游线圈的占有率标准差，%;X6为上下游线圈速度差的绝对值，km/h.

t 检验用来检验RTCI 表达式中各个解释变量在事故组和非事故组中是否存在显著差异.表1给出了各个变量的描述性统计分析和t 检验的结果.所有t 检验都高度显著，表明各个解释变量在事故组和非事故组中都存在显著差异.

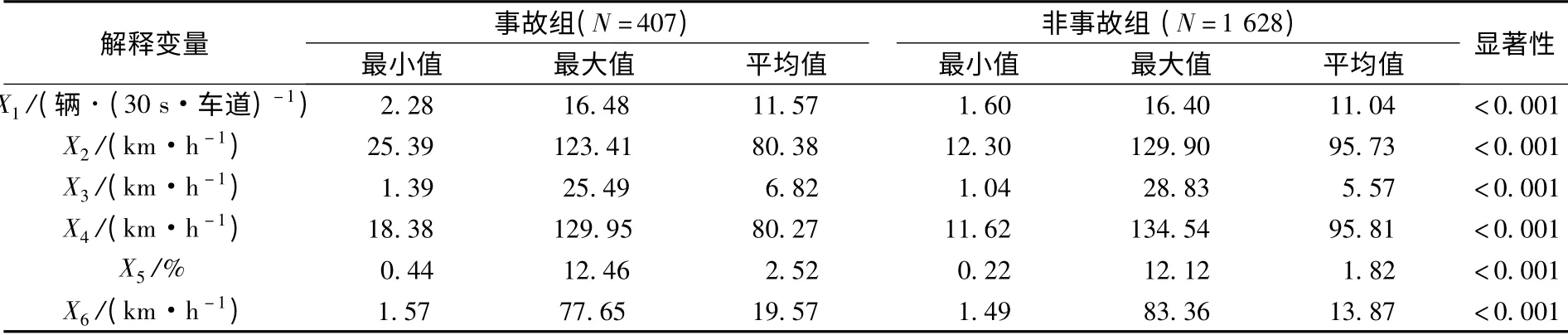
表1 解释变量的描述性统计分析和t 检验结果

RTCI 的阈值为事故组和非事故组形心(group centroids)的加权平均值.事故组和非事故组形心分别为－0.539 和0.135，因而RTCI 判别危险交通流特征的阈值为－0.54 +0.135 ×4 =0.即当RTCI ＜0 时，代表危险交通流状态，有可能导致交通事故的发生;当RTCI ＞0 时，代表正常交通流状态，处于较安全状态.

3.2 预测精度

表2给出了RTCI 值对高速公路交通事故的预测精度.在训练样本中，63.4%的事故样本被成功预测，68.0%的非事故样本被成功预测.这表明Fisher 判别分析对训练样本有较好的拟合精度.在验证样本中，RTCI 值在102 个事故样本中预测了67 个事故，在408 个非事故样本中预测了268 个非事故.RTCI 值对验证样本的总预测精度达到65.7%，表明RTCI 值在高速公路交通事故预测方面有较好的精度.总样本中事故和非事故样本的比例为1∶4，从总样本中随机抽取一个样本，该样本是事故的概率为20%.相对于随机选取，RTCI 值可以将事故预测精度从20%提高到65.7%.

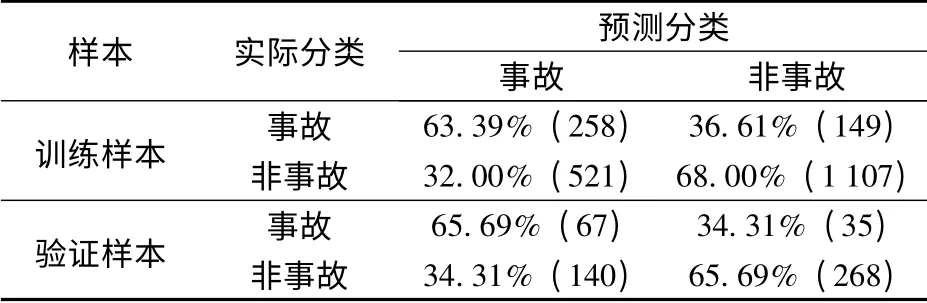
表2 RTCI 事故预测精度

3.3 RTCI 值与事故风险的关系

为了利用RTCI 实时评价高速公路交通安全状况，还需量化RTCI 与交通事故风险之间的定量关系.本文采用条件logistic 回归方法量化RTCI对交通事故风险的影响，将由式(4)计算得到的RTCI 值作为条件logistic 回归的解释变量.条件logistic 回归的估计结果表明，RTCI 值对交通事故风险有显著影响.RTCI 的系数为－1.031，表明RTCI 值越小，发生交通事故的概率越大.RTCI 的比值比(odds ratio)代表RTCI 每增加1 个单位对交通事故风险的影响，计算公式如下:

因而比值比OR =eβ1=0.357，比值比的倒数e－β1=2.803，代表RTCI 每减小1 个单位，交通事故风险将提高1.8 倍.

下面以实例简要说明RTCI 在实时评价高速公路交通安全方面的应用.如研究路段上的594 号事故发生在2010年5月21日8:38，该起事故发生地点当天RTCI 值的变动如图4所示.RTCI 值在8:17 开始持续下降，表明此时的事故风险在逐渐增加.从8:17 到该起事故的发生时间8:38，RTCI值从0.57 下降到－1.73，表明在8:38 时的事故风险是8:17 时的10.7 倍(2.803(0.57－(－1.73)).在事故发生之后RTCI 继续下降，表明事故风险继续增加，有引起二次交通事故的危险性.

图4 RTCI 值的变化与交通事故的发生

4 结语

利用高精度交通流数据建立了高速公路交通安全实时评价指标，并用于交通事故实时预测.采用Fisher 判别分析方法，建立实时交通流参数的线性组合以判别危险交通流状态，该线性组合被定义为RTCI.研究结果表明，该指标对交通事故的预测精度为65.7%，且该指标减小1 个单位，交通事故风险将增大1.8 倍.RTCI 值可作为高速公路实时事故风险的间接评价指标，用于动态交通控制系统中实时评价交通安全状况.但是在工程实践应用之前，还需要研究交通事故与RTCI 值之间的关系，探索RTCI 值减小带来事故风险增加的原因.另外，由于国内高速公路现有数据不能满足建立RTCI 的要求，本文选用了美国加州I-880 N 高速公路数据进行研究，因而还需利用未来国内高速公路的高精度交通流数据进一步测试该指标的性能.

References)

［1］Lord D，Manar A，Vizioli A.Modeling crash-flowdensity and crash-flow-V/C ratio for rural and urban freeway segments［J］.Accident Analysis and Prevention，2005，37(1):185-199.

［2］El-Basyouny K，Sayed T.Comparison of two negative binomial regression techniques in developing accident prediction models ［J］.Transportation Research Record，2006，1950:9-16.

［3］Hiselius L W.Estimating the relationship between accident frequency and homogeneous and inhomogeneous traffic flows ［J］.Accident Analysis and Prevention，2004，36(2):149-163.

［4］Greibe P.Accident prediction models for urban roads［J］.Accident Analysis and Prevention，2003，35(3):273-285.

［5］Memon A Q.Road accident prediction models and the influence of traffic flow，road length，road class and vehicle class on accidents ［C/CD］//Proceedings of the 87th Annual Meeting of the Transportation Research Board.Washington DC，2008.

［6］钟连德，孙小端，陈永胜，等.高速公路V/C 与事故率关系研究［J］.北京工业大学学报，2007，33(1):33-40.

Zhong Liande，Sun Xiaoduan，Chen Yongsheng，et al.Research on the relationship between V/C and crash rate on freeway［J］.Journal of Beijing University of Technology，2007，33(1):33-40.(in Chinese)

［7］崔红军，魏连雨，庞建勋.道路条件与交通安全的研究方法［J］.西安公路交通大学学报，2001，21(4):36-39.

Cui Hongjun，Wei Lianyu，Pang Jianxun.Research method of road condition and traffic accident［J］.Journal of Xi′an Highway University，2001，21(4):36-39.(in Chinese)

［8］Abdel-Aty M，Uddin N，Abdalla F，et al.Predicting freeway crashes based on loop detector data using matched case-control logistic regression［J］.Transportation Research Record，2004，1897:88-95.

［9］Abdel-aty M，Uddin N，Pande A.Split models for predicting multi-vehicle crashes during high-speed and lowspeed operating conditions on freeways［J］.Transportation Research Record，2005，1908:51-58.

［10］Abdel-Aty M，Pande A.Identifying crash propensity using specific traffic speed conditions［J］.Journal of Safety Research，2005，36(1):97-108.

［11］Oh J，Oh C，Ritchie S，et al.Real-time estimation of accident likelihood for safety enhancement［J］.Journal of Transportation Engineering，2005，131(5):358-363.

［12］Oh C，Oh J，Ritchie S.Real-time hazardous traffic condition warning system:framework and evaluation［J］.IEEE Transactions on Intelligent Transportation Systems，2005，6(3):265-272.

［13］Lee C，Saccomanno F，Hellinga B.Analysis of crash precursors on instrumented freeways［J］.Transportation Research Record，2002，1784:1-8.

［14］Lee C，Hellinga B，Saccomanno F.Real-time crash prediction model for application to crash prevention in freeway traffic［J］.Transportation Research Record，2003，1840:67-77.

［15］Hossain M，Muromachi Y.Evaluating location of placement and spacing of detectors for real-time crash prediction on urban expressways ［C/CD］//Proceedings of the 89th Annual Meeting of the Transportation Research Board.Washington DC，2010.

［16］Zheng Z，Ahna S，Monsere C.Impact of traffic oscillations on freeway crash occurrences ［J］.Accident Analysis and Prevention，2010，42(2):626-636.

［17］张文彤.SPSS11 统计分析教程［M］.北京:北京希望电子出版社，2002:177-189.