基于EMD－小波随机消噪模型的GPS/INS组合导航

王 坚 李增科 高井祥 王金岭

(1 中国矿业大学国土环境与灾害监测国家测绘局重点实验室，徐州221116)

(2 中国矿业大学环境与测绘学院，徐州221116)

(3 澳大利亚新南威尔士大学测绘与空间信息学院，澳大利亚悉尼2052)

优化导航模型及误差补偿算法是提高GPS/INS(global positioning system/inertial navigation system)组合导航精度的主要方式.陀螺仪及加速度计除受到元件本身固有观测精度的影响，INS 原始观测数据还受到系统协同作用带来的高频噪声的影响，导致导航精度降低，已引起国内外学者们的广泛关注［1］.引入新的数据处理理论，发展精度更高的导航模型具有重要研究意义.Nassar［2］采用高阶AR 模型，比较了Yule－Walker 法、协方差法和Burg 法在AR 模型参数求取方面的优劣.吴富梅等［3］将小波阈值消噪引入GPS/INS 组合导航，对观测数据进行消噪预处理.Guo 等［4］设计Butterworth 低通滤波对INS 原始数据滤波，消除了高频噪声，得到更高精度的观测数据.上述模型都可明显提高GPS/INS 组合导航系统的定位精度.本文在分析INS 原始观测数据误差源的基础上，利用经验模态分解的自适应和完全数据驱动的特征，提出INS 随机误差的经验模态小波分解模型，提高了GPS/INS 组合导航的精度.实测数据分析表明了本文方法的有效性.

1 系统误差分析

从频域的角度，可清晰地描述GPS/INS 组合系统的误差分布及建模过程［5－6］.根据文献［5］的研究，组合系统的误差可分为长周期与短周期误差，如图1所示，其中fs为采样频率.通过组合导航算法及INS 计算可消除大部分误差项(见图2)，但由于导航算法及模型线性化等原因，仍存在残余的长周期及短周期误差.文献［5］通过采用滤波方法对INS 原始数据滤波，预先消除残余误差，提高了导航精度.

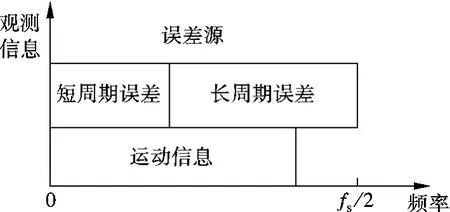
图1 GPS/INS 组合系统的误差分析［5］

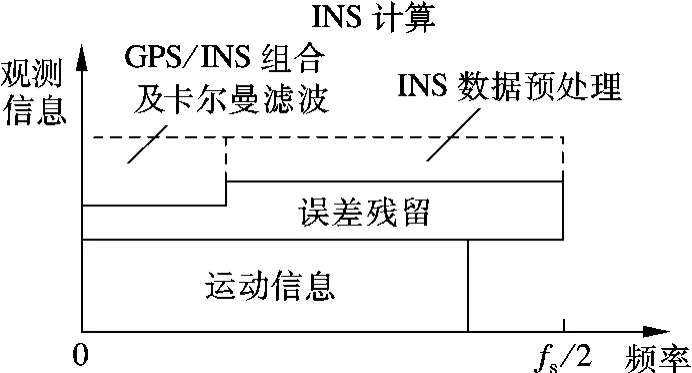
图2 误差消除后的数据信息［5］

2 组合导航模型

本文中惯性导航系统模型采用的状态参数为24 维，包括9 个导航解误差(xnav)、6 个加速度误差模型参数(xacc)、3 个陀螺漂移(xgyro)、3 个重力误差(xgrav)及3 个天线误差(xant，由GPS 天线与INS 间的杆臂效应造成)［7-8］.载体运动过程中杆臂效应变化很小，在本模型中将杆臂效应作为偏心常数处理:

式中，δrN，δrE，δrD为位置误差;δvN，δvE，δvD为速度误差;δψN，δψE，δψD为姿态误差;▽bx，▽by，▽bz为加速度偏心;▽fx，▽fy，▽fz为加速度尺度因子;εbx，εby，εbz为陀螺漂移;δgN，δgE，δgD为重力误差;δLbx，δLby，δLbz为天线误差.

状态转移矩阵表达式为

式中，F 为系统状态转移矩阵;w 为系统噪声矩阵.

取GPS 和INS 输出的位置之差作为观测值，构造观测量z(t)［9］:

式中，rGPS(t)为GPS 的位置观测值;rINS(0)，vINS(0)为INS 的初始位置和速度;α(t)为INS 所测得的加速度;rINS(t)为INS 的位置计算值.则卡尔曼量测方程为

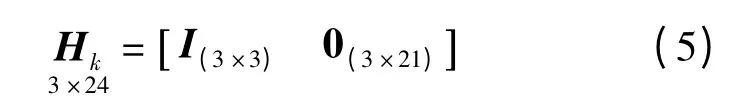
式中，Hk为观测矩阵;xk为状态矩阵;vk为观测噪声，满足高斯白噪声特性.

3 EMD-小波随机消噪模型

3.1 经验模态分解

EMD 将信号分解为满足以下条件的固有模态函数(intrinsic mode function，IMF)［10］:①零点数目与极值点数目相同或至多相差1;②函数关于局部平均对称.最终将信号表示成若干IMF 与单调残差函数的和.一维信号x(t)的分解可表示为

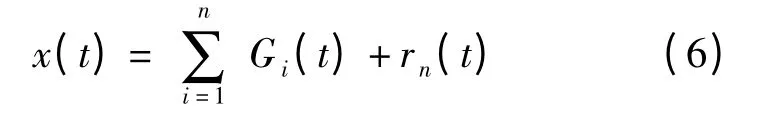
式中，Gi(t)表示第i 个IMF;rn(t)为单调残差函数.EMD 算法采用所谓的“筛”完成，基本步骤为:

①求取信号x(t)的极值点;

②分别由极小值点与极大值点得包络线emin(t)和emax(t);

③计算上下包络的平均值emean(t)=(emin(t)+emax(t))/2;

④提取细节d(t)=x(t)－emean(t);

⑤令x(t)=d(t)，重复进行步骤①～④，直到d(t)为零均值，此时得到的d(t)即为一个IMF;

⑥计算残差m(t)=x(t)－Gi(t);

⑦重复运算直到残差不含IMF 函数.

对EMD 分解过程进一步进行多尺度描述，定义EMD 求取IMF 的算子与求取残差的算子分别为Fimf(·)与Fres(·)，则这2 个算子定义了类似高频滤波与低频滤波的过程.Fimf(·)算子包括EMD 分解过程的步骤①～⑤，获得该尺度的高频部分;Fres(·)指步骤⑥，计算对应分解尺度的残差，即对应尺度的低频部分.对低频部分可继续进行分解，从而实现多尺度的分解过程.原始第0 层尺度信号x0(t)采用原始信号x(t)表示，第i 尺度到第i+1 尺度的分解式可表示为

重构式为

与基于滤波器的分析技术不同，此方法引入极值点距离进行局部尺度的确定，使得分解具有自适应和完全数据驱动的特征.EMD 结果表明这种分解过程是符合物理意义的，可得到近似周期，分解的经验模态量满足瞬时频率特征(Hilbert 谱)分析的条件，便于分析信号的瞬时特征用于特征提取.

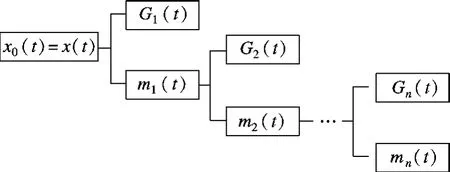
图3 EMD 多尺度分解结构示意图

3.2 EMD－小波模型

基于EMD 与小波降噪模型［11］，提出INS 原始观测数据的随机消噪模型.首先，对观测数据(三轴速度增量及三轴角速度)x(t)进行EMD 分解，得到时变但平稳的单分量信号;其次，确定高频IMF(根据需要可以选择不同数量的IMF)进行小波降噪［12］，发挥小波降噪对平稳含噪信号的处理能力［13］，本文选择前5 个IMF 进行小波阈值滤波去噪;最后，将降噪后的IMF 与没有经过去噪的IMF 相加获得重构后的信号［14－15］.图4给出基于EMD 的小波阈值降噪流程图，其中，imfi(i =1，2，…，n)为经验模态各分解层的模量，^x(t)为经过小波EMD 阈值降噪后的数据信号.

图4 EMD 与小波降噪模型

为确定高频IMF，定义如下尺度标准化模量的累积均值［16］:

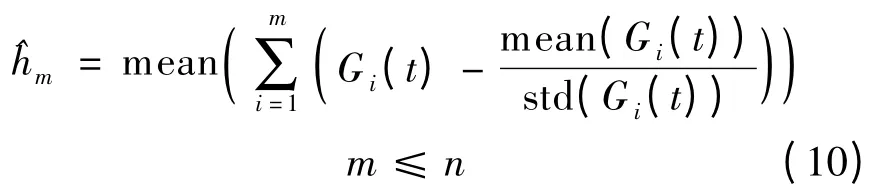
式中，mean(Gi(t)为Gi(t)的平均值;std(Gi(t))为Gi(t)的标准差.如果偏离零值，则尺度m 之前的模态分量为高频IMF.从信号中提取的趋势项可由下式给出［17］:

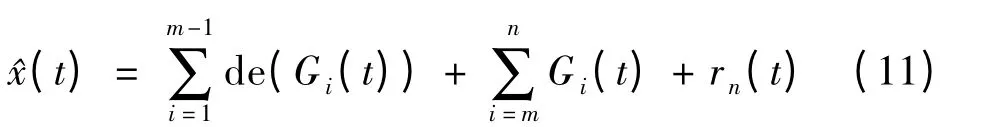
式中，de(·)表示小波消噪.EMD 滤波去噪法与小波方法都能最大限度地削弱测量的随机误差，但EMD 滤波去噪比小波方法更直接，且不受测不准原理及小波函数选择的影响［18］，当噪声较大时小波去噪稳定性略优于EMD.将两者有效结合，更能发挥EMD 的自适应和完全数据驱动的特征，增强滤波效果［19］.

4 基于EMD-小波的组合导航技术路线

引入EMD［20］－小波模型，提出基于EMD－小波消噪的GPS/INS 组合导航技术路线［21－22］(见图5).首先采用GPS 观测的1 Hz 和2 Hz 的数据求解动态导航解，并对前一历元及本历元间100 Hz的INS 原始观测数据累积，然后采用EMD－小波消噪模型对累积的INS 原始观测数据去除高频噪声，对消噪后的数据进行INS 导航计算，得到位置和速度解.最后采用GPS 及INS 计算结果进行导航系统误差计算，通过闭环反馈，实现导航解求解.为验证EMD－小波方法的滤波效果，滤波前后GPS/INS 组合导航Kalman 滤波器选用相同的滤波参数.

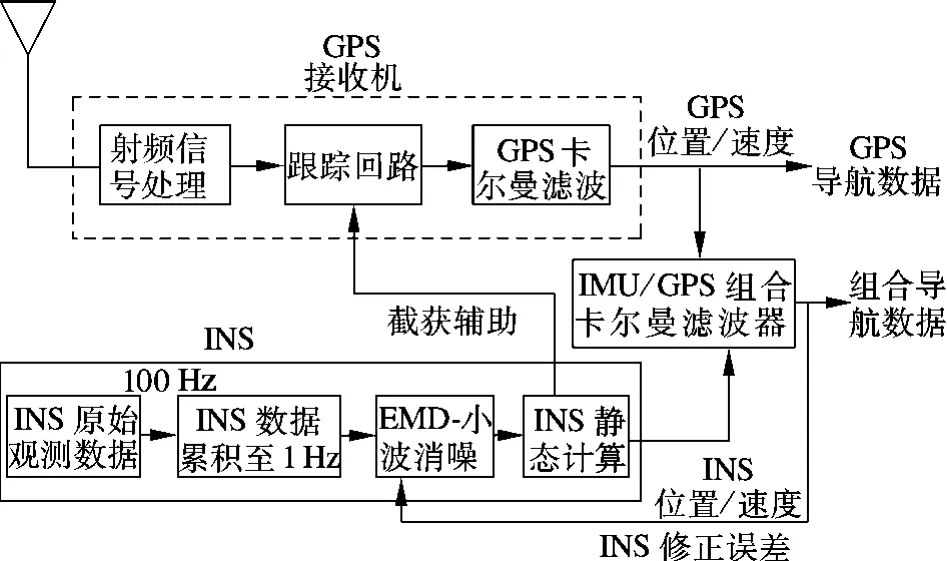
图5 基于EMD-小波的组合导航

5 实例分析

运用本文提出的组合导航技术路线对实测数据进行分析，数据采集于2005年新南威尔士大学校园.陆用车辆分别在一个大范围和相对较小的范围按相同轨迹作重复运动.整个载体运动较为平滑，但在拐弯处和小范围内运动时载体状态变化较大.采用2 台徕卡530GPS 接收机和1 台DQI－NP惯性测量单元进行实验.其中，1 台接收机架设在已知点上作为静止参考基站，另1 台接收机作为流动站和惯性测量单元一起安置在运动车辆顶端.DQI－NP 惯性测量单元的陀螺偏心和尺度因子分别为5(°)/h，500 ×10－6;加速度计的偏心和尺度因子分别为5 ×10－4g，800 ×10－6.INS 采集频率为100 Hz，GPS 采样周期为1 s，为对比滤波对INS 导航算法精度的影响，更新周期分别选用1 s 和2 s［23］.

采用经验模态分解原始观测数据，以Z 方向的角速度观测值(见图6(a))为例说明INS 观测数据的分离过程.首先对Z 方向的加速度观测序列进行11 个尺度的分解，得到11 个模量与1 个趋势项(见图7).根据尺度标准化模量的累积均值确定前5 个分量为序列的高频部分，运用小波消噪处理1～5 模量(imf1～imf5)，消噪后的结果如图8所示.小波消噪后模态分量(imf′1～imf′5)替代消噪前的模态分量(imf1～imf5)，并与趋势项重构，形成消噪后的观测数据(见图6(b)).

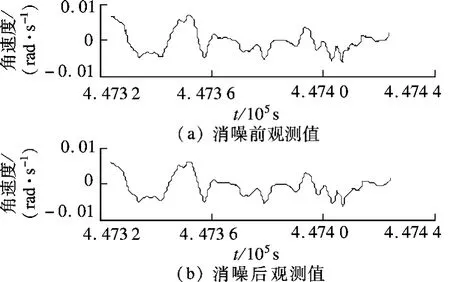
图6 Z 方向角速度观测值

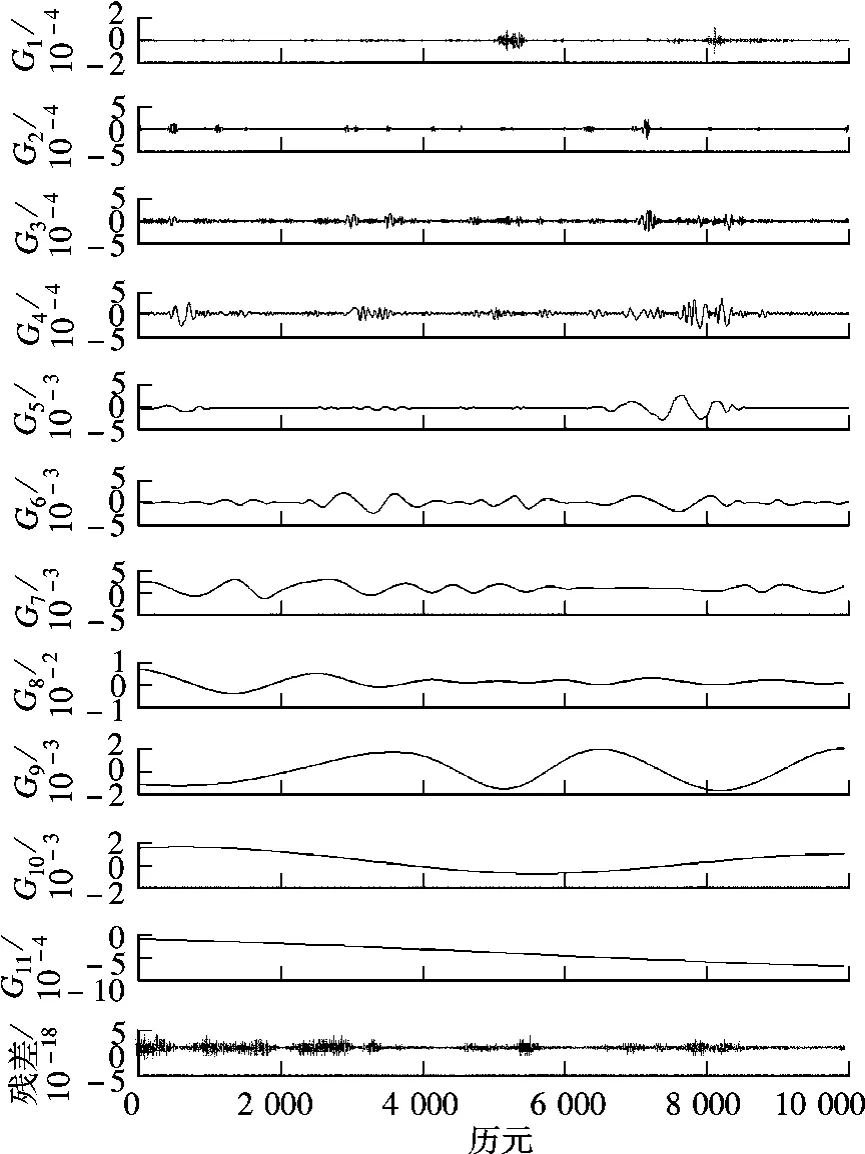
图7 Z 方向角速度的EMD 分解

根据图5进行组合导航计算，图9(a)是组合周期为1 s 时导航计算值和参考值(RTK 值)的陆地运动轨迹比较图，图9(b)、(c)、(d)分别是在X，Y，Z 方向上导航计算值与参考值的比较.

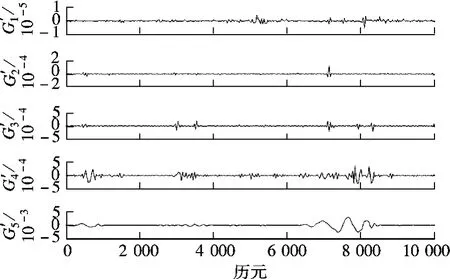
图8 基于EMD 的小波消噪

图9 组合导航运动轨迹比较

在更新周期内，将滤波前后INS 自主导航计算值和GPS－RTK 参考值比较，求得两者的差值.图10和图11分别是组合周期为1 s 和2 s 时，滤波前后自主导航值和参考值的残差.从图10和图11可看出，相对于滤波前，经过EMD 小波消噪后的残差值更接近于0，说明通过基于EMD 的小波消噪消除INS 中的误差来提高自主导航精度是可行的，从而能够进一步提高GPS/INS 组合导航精度.

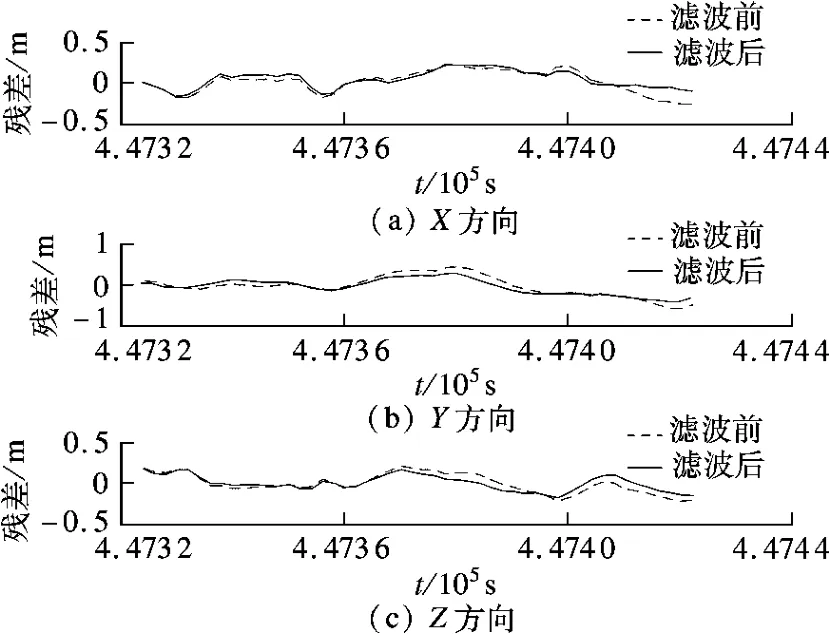
图10 导航计算值的残差值(组合周期为1 s)

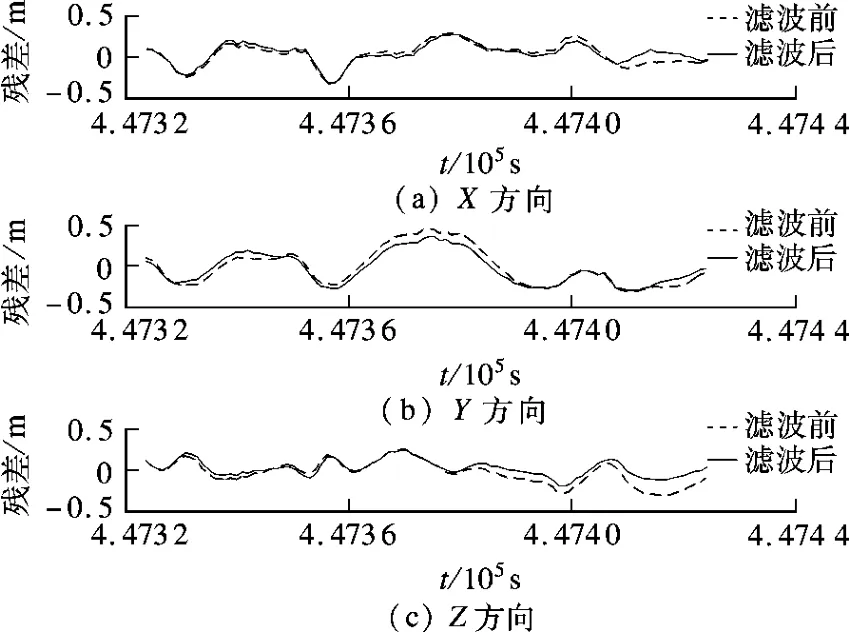
图11 导航计算值的残差值(组合周期为2 s)

表1和表2分别是组合周期为1 s 和2 s 时滤波前后的位置误差比较.通过比较两者的均方根误差，可以看出滤波后的导航解要优于滤波前.组合周期为1 s 时，X，Y，Z 方向上导航精度分别提高了9.07%(11 mm)、13.89%(30 mm)、35.14%(50 mm)，残差最大值在3 个方向上分别减小了2.62%(9 mm)、19.54%(78 mm)、31.23%(100 mm);组合周期为2 s 时，X，Y，Z 方向上导航精度分别提高了17.82%(24 mm)、23.46%(60 mm)、22.48%(27 mm)，残差最大值在3 个方向上分别减小了14.34%(36 mm)、28.85%(160 mm)、17.48%(42 mm).以上实验结果表明，通过小波滤波可以有效地消除INS 原始观测数据的噪声，从而提高组合导航精度.图12给出更新周期为1 s 时，在GPS 的447 416 和447 417 历元之间，滤波前后INS 自主导航解在X，Y，Z 方向的对比图.由于这些数据是在导航过程中截取的，因此存在一个初始差值.可以看出，随着时间的推移，消噪前后的导航解的差值不是定值，而是有增大的趋势，说明EMD－小波模型在消噪过程中取得了良好的效果.

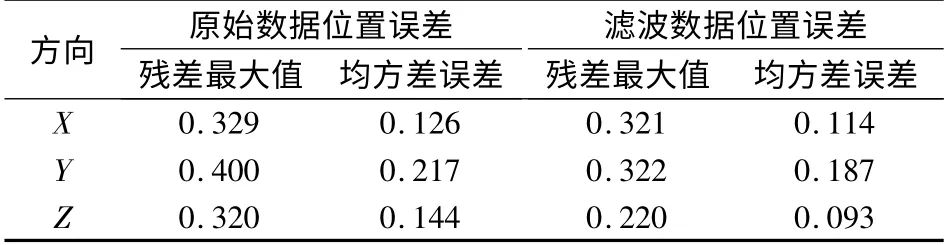
表1 滤波前后的位置误差(组合周期为1 s)m

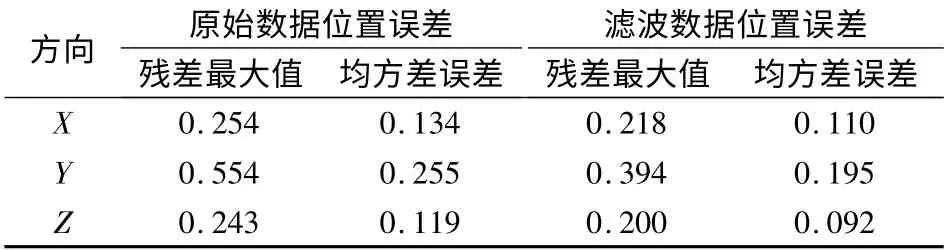
表2 滤波前后的位置误差(组合周期为2 s)m

图12 INS 导航解比较

为进一步研究本文模型在不同GPS 中断情况下对组合导航精度的影响，在数据处理过程中分别设置4 s 和6 s 的GPS 中断，即GPS 对数据的更新周期为4 s 和6 s，结合前述组合周期为1 s 和2 s的实验，比较各中断周期在X，Y，Z 方向上的精度提高情况，结果如表3所示.

表3 不同GPS 中断时间滤波前后的精度提高 %

由表3可看出，对于不同的GPS 中断时间，EMD－小波滤波方法对位置解算精度提高都起到了一定的效果.当中断时间较短时(1 s 和2 s)，滤波效果比较明显;中断时长增加(4 s 和6 s)，滤波效果有明显减弱.随着INS 自主导航时间变长，偏心等误差产生积累，成为影响INS 解算精度的主要因素，而随机误差的影响减弱.说明在GPS 信号产生中断，INS 自主导航过程中，既需要削弱随机噪声，又应减少系统误差的积累，从而更好地提高导航精度.

6 结语

在分析GPS/INS 组合系统的误差特性基础上，提出基于EMD－小波模型的GPS/INS 组合导航技术路线，并通过实测数据验证了模型的可行性.试验数据计算表明，采用本文模型在INS 原始观测数据消噪的基础上，再进行组合导航计算能明显提高导航精度.但由于EMD－小波模型实时计算需要在导航过程中采用滑动的方法对INS 数据进行累积，然后降噪，因而增加了导航的计算复杂度.

References)

［1］Hasan A M，Samsudin K，Ramli A R，et al.A review of navigation systems(integration and algorithms)［J］.Australian Journal of Basic and Applied Sciences，2009，3(2):943－959.

［2］Nassar S.Improving the inertial navigation system(INS)error model for INS and INS/DGPS applications［D］.Calgary，Canada:Department of Geomatics Engineering，University of Calgary，2003.

［3］吴富梅，杨元喜.基于小波阈值消噪自适应滤波的GPS/INS 组合导航［J］.测绘学报，2007，36(2):124－128.

Wu Fumei，Yang Yuanxi.GPS/INS integrated navigation by adaptive filtering based on wavelet threshold de－noising［J］.Acta Geodaetica et Cartographica Sinica，2007，36(2):124－128.(in Chinese)

［4］Guo H，Yu M，Liu J，et al.Butterworth low－pass filter for processing inertial navigation system raw data［J］.Journal of Surveying Engineering，2004，130(4):175－178.

［5］Bruton A M，Schwarz K P，Skaloud J.The use of wavelets for the analysis and de－noising of kinematic geodetic measurements［C/CD］//Proceedings of the IAG Symposia.Birmingham，UK，2000.

［6］Skaloud J.Optimizing georeferencing of airborne survey systems by INS/DGPS［D］.Calgary，Canada:Department of Geomatics Engineering，University of Calgary，1999.

［7］Titterton D H，Weston J L.Strapdown inertial navigation technology［M］.2nd ed.Lexington，MA，USA:MIT Lincoln Laboratory，2004.

［8］秦永元.卡尔曼滤波与组合导航原理［M］.西安:西北工业大学出版社，1998.

［9］万振刚，周百令，马云峰，等.自适应联合H∞滤波器及其在组合导航系统中的应用［J］.东南大学学报:自然科学版，2004，34(5):623－626.

Wan Zhengang，Zhou Bailing，Ma Yunfeng，et al.Adaptive federated H∞filter and its application in integrated navigation system［J］.Journal of Southeast University:Natural Science Edition，2004，34(5):623－626.(in Chinese)

［10］王坚，高井祥，王金玲.基于经验模态分解的GPS 基线解算模型［J］.测绘学报，2008，37(1):10－14.

Wang Jian，Gao Jingxiang，Wang Jinling.GPS baseline solution based on empirical mode decomposition［J］.Acta Geodaetica et Cartographica Sinica，2008，37(1):10－14.(in Chinese)

［11］章飞，周杏鹏，陈小惠.基于小波变换的粒子滤波目标跟踪算法［J］.东南大学学报:自然科学版，2010，40(2):320－325.

Zhang Fei，Zhou Xingpeng，Chen Xiaohui.Particle filter target tracking algorithm based on wavelet transform［J］.Journal of Southeast University:Natural Science Edition，2010，40(2):320－325.(in Chinese)

［12］吴富梅，杨元喜.基于小波变换和序贯抗差估计的捷联惯导初始对准［J］.武汉大学学报:信息科学版，2007，32(7):617－620.

Wu Fumei，Yang Yuanxi.SINS initial alignment based on wavelet transform and sequential robust adjustment［J］.Geomatics and Information Science of Wuhan University，2007，32(7):617－620.(in Chinese)

［13］Jin W，Zhang G，Hu L.Radar emitter signal recognition using wavelet packet transform and support vector machines［J］.Journal of Southwest Jiaotong University，2006，14(1):15－22.

［14］Ingle V K，Proakis J G.Digital signal processing using MATLAB［M］.New York:PWS Publishing Company，1997.

［15］李振兴，徐洪洲.基于经验模态分解的小波阈值降噪方法研究［J］.计算机仿真，2009，26(9):325－328.

Li Zhenxing，Xu Hongzhou.A wavelet threshold denoising algorithm based on empirical mode decomposition［J］.Computer Simulation，2009，26(9):325－328.(in Chinese)

［16］Flandrin P，Gonçalvès P，Rilling G.Detrending and denoising with empirical mode decompositions［C］//12th European Signal Processing Conference.Vienna，Austria，2004.

［17］杜修力，何立志，侯伟.基于经验模态分解(EMD)的小波阈值除噪方法［J］.北京工业大学学报，2007，33(3):265－272.

Du Xiuli，He Lizhi，Hou Wei.A study of wavelet threshold denoising based on empirical mode decomposition(EMD)［J］.Journal of Beijing University of Technology，2007，33(3):265－272.(in Chinese)

［18］戴吾蛟，丁晓利，朱建军，等.基于经验模式分解的滤波去噪法及其在GPS 多路径效应中的应用［J］.测绘学报，2006，35(4):321－327.

Dai Wujiao，Ding Xiaoli，Zhu Jianjun，et al.EMD filter method and its application in GPS multipath［J］.Acta Geodaetica et Cartographica Sinica，2006，35(4):321－327.(in Chinese)

［19］Wang J，Wang J，Roberts C.Reducing GPS carrier phase errors with EMD－wavelet for precise static positioning［J］.Survey Review，2009，41(312):152－161.

［20］Huang N，Shen Z，Long S，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non－stationary time series analysis［J］.Proceedings of the Royal Society，1998，454(1971):903－995.

［21］杨元喜.自适应动态导航定位［M］.北京:测绘出版社，2006.

［22］Han S，Wang J.Land vehicle navigation with the integration of GPS and reduced INS:performance improvement with velocity aiding［J］.Journal of Navigation，2010，63(1):153－166.

［23］Ding W，Wang J，Chris R.Improving covariance based adaptive estimation for GPS/INS integration［J］.Journal of Navigation，2007，60(3):517－529.