转子－轴承－密封系统的多因素动力行为研究＊

王 弢 帅 健 刘焰明

（武汉理工大学能源与动力工程学院1） 武汉 430063） （中国石油大学机电学院2） 北京 102249）

转子－轴承－密封系统中，诸多影响转子系统的动力学行为及其振动状态的因素已经逐渐得到人们的重视，对于诸如发电机组、船舶推进轴系等旋转机械，其中的动密封装置，例如迷宫密封、机械端面密封等，已有一些学者进行了相关的研究［1－3］，而机械端面密封对于转子振动特性的研究鲜见文献资料报道，但是，机械密封动静环之间的密封液膜产生的密封力对转子动力学行为的影响是不容置疑的［4－7］．本文将就转子－轴承－密封系统开展相关研究．

1 转子－轴承－密封系统动力学方程

采用短轴承支撑的刚性Jeffcott转子．图1为转子－圆盘－机械密封系统，假定转子为单圆盘系统，两端支撑在滑动轴承上，油膜力fx，fy作用在左轴承处轴颈上，油膜力，，密封力Fx，Fy作用在右轴承处轴颈上．

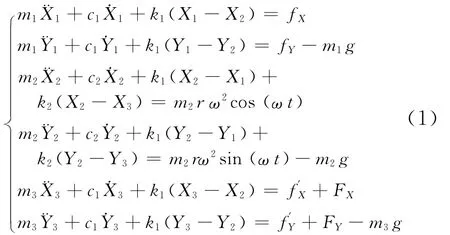
式中：m1为左轴承处轴颈质量；m2为圆盘质量；m3为右轴承处轴颈质量；c1，c2分别是轴承与圆盘处结构阻尼；k1，k2分别为圆盘两侧转轴的刚度；c为轴承间隙；x1，y1为左侧轴颈位移；x2，y2为圆盘位移；x3，y3为右侧轴颈位移；r为圆盘质量偏心距；ω为转子转动角速度．Fx，Fy为动静环之间液膜对转轴X，Y方向的合力．

本文中，密封力采用Muszynska模型．

油膜力fx，fy采用短轴承非线性油膜力模型，表达式为

图1 非线性转子－轴承－密封系统

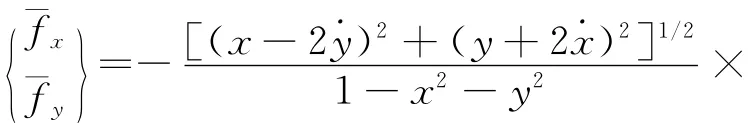
2 数值计算结果分析

假定系统的参数：m1为100kg；m2为80kg；m3为300kg；右轴承半径为40mm、长度为200mm；左轴承半径为60mm、长度为60mm；轴颈间隙为0．2mm；圆盘质量偏心为0．06mm；轴承结构阻尼c1为5 000N·s·m－1；圆盘结构阻尼c2为2 000N·s·m－1；润滑介质粘度为0．018Pa·s，圆盘左侧转轴刚度k1为1×107N／m；右侧转轴刚度k2为1×107N／m．

以右轴承为例分析，图2为轴颈中心分岔图，当转速过低时，转子作周期运动，ω＝150rad／s时的轴心轨迹图，poincare映射图如图3所示．当ω＝247rad／s时，转子进入拟周期运动，其轴心轨迹图，poincare映射图如图4所示，当ω＝330 rad／s时，转子进入3倍周期运动，轴心轨迹图，poincare映射图如图5所示，当ω＝361rad／s时，转子进入混沌运动，轴心轨迹图，poincare映射图如图6所示，当ω＝464rad／s时，转子进入5倍周期运动，轴心轨迹图，poincare映射图如图7所示，当ω＝481rad／s时，转子进入倍周期运动，轴心轨迹图，poincare映射图如图8所示，当ω＝625rad／s时，转子进入拟周期运动，轴心轨迹图，poincare映射图如图9所示．

图2 轴颈中心分岔图

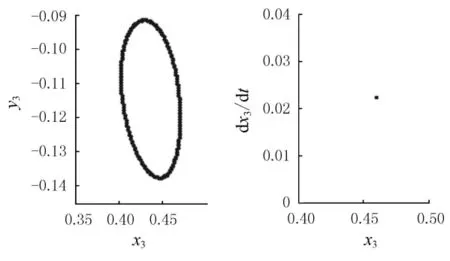
图3 轴颈中心轨迹图、poincare映射图（ω＝150rad／s）

图4 轴颈中心轨迹图、poincare映射图（ω＝247rad／s）

图5 轴颈中心轨迹图、poincare映射图（ω＝330rad／s）

图6 轴颈中心轨迹图、poincare映射图（ω＝361rad／s）

图7 轴颈中心轨迹图、poincare映射图（ω＝464rad／s）

图8 轴颈中心轨迹图、poincare映射图（ω＝481rad／s）

图10 为ω＝330rad／s时轴颈中心振幅随密封压差变化图，当密封内外压差增大时，轴颈中心的振幅逐渐减小，当p＝0．2MPa时，发生3倍周期分岔，当压差增大达到0．48MPa时，系统发生12倍周期分岔，当压差继续增大到0．67MPa时，振幅不再增大，此时通过增大压差来抑制转子的振动已经没有意义．

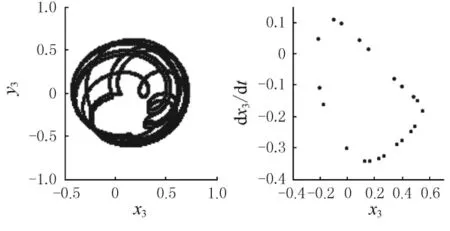
图9 轴颈中心轨迹图、poincare映射图（ω＝625rad／s）

图10 轴颈中心轨迹与压差的变化关系

图11 为ω＝330rad／s时右轴颈中心振幅随圆盘质量偏心的变化图，当偏心率逐渐增大时，轴颈中心振幅首先逐渐减小，然后逐渐增大，并随之发生分岔行为，可能进一步导致混沌运动的产生，造成系统的不稳定．

图11 轴颈中心轨迹与圆盘质量偏心的变化关系

3 结 论

1）转子－轴承－密封系统在一定的偏心率作用下随转速的增加具有产生混沌运动的能力，混沌运动容易引起系统产生失稳并可能导致疲劳损坏，因此设计时应该避免．

2）增加密封内外压差降会促进转子的稳定，但过大的密封压差不仅没有现实意义，而且还会对工作环境带来更高的要求．

3）随着偏心量的增大，系统将会发生分岔，变得不稳定．

［1］李松涛，许庆余．迷宫密封－滑动轴承－转子系统的非线性动力稳定性［J］．航空学报，2003，24（3）：1－5．

［2］叶建槐，刘占生．非线性转子－密封系统稳定性与分岔［J］．航空动力学报，2007，22（5）：1－3．

［3］陈予恕，于 千，侯书军．非线性转子－密封系统的稳定性和 Hopf分岔［J］．振动工程学报，1997，10（3）：1－4．

［4］徐 华，朱 均．机械密封对转子轴承系统动力学性能的影响［J］．西安交通大学学报，2004，38（7）：1－3．

［5］李 永．转子－轴承－密封系统的非线性振动与分岔［D］．大连：大连理工大学，2007．

［6］武新华，张新江，薛小平，等．弹性转子－轴承系统的非线性动力学研究［J］．中国机械工程，2001，12（11）：1221－1224．

［7］杨令康，朱汉华，贺立峰．转子－轴承系统的润滑与碰摩特性分析［J］．武汉理工大学学报：交通科学与工程版，2011，35（3）：595－598．