基于任务安全性的亚轨道飞行器返回轨迹优化

王文虎，李新国

(西北工业大学航天学院，陕西西安 710072)

引言

对于可重复使用的亚轨道飞行器(Suborbital Launch Vehicle，SLV)返回段而言，首要任务就是能够安全返回地面。因而，从安全性角度出发，进行返回轨迹优化是非常必要的。文献［1-2］提出的方法都对动力学模型进行了降阶处理，虽然简化了返回问题的复杂性、加快了轨迹生成的速度，但文献［3］指出模型降阶处理会降低任务的安全性。

本文针对亚轨道飞行器，采用高斯伪谱法进行了基于任务安全性的返回轨迹优化研究，并验证了可行性与最优性。为了增加任务的安全性，动力学模型考虑地球旋转影响;为了满足实际控制能力约束，利用伪控制量作为控制变量;在考虑终端约束及性能指标时引入“末端进场走廊”(Final Approach Corridor，FAC)，摒弃了传统再入分段、末端区域能量管理(TAEM)段、航向校正圆锥(HAC)等概念，实现了从初始状态到自动着陆界面全程轨迹优化。

1 高斯伪谱法

近年来，随着计算机技术的快速发展、求解大规模稀疏非线性规划问题(NLP)算法的逐步成熟和伪谱法的出现，为快速、准确地进行飞行器轨迹优化提供了有效途径。

伪谱法是一种正交配点法，因其求解精度高、收敛速度快、具有很好的鲁棒性而备受关注［4］。常见的伪谱法包括:勒让德伪谱法(LPM)、拉道伪谱法(RPM)和高斯伪谱法(GPM)。Huntington［4］对三种伪谱法在精度和计算效率等方面进行了比较，结果表明高斯伪谱法具有更高的求解精度和收敛速度，并且在处理含初始和终端约束的问题上具有优势。高斯伪谱法基本原理如图1所示。

图1 高斯伪谱法基本原理示意图

在时域(－1，1)内选 Legendre-Gauss(LG)点作为配点。LG点与初始、末端时刻点构成最优控制问题的离散点，将状态变量和控制变量在这些点上离散。以初始时刻点与LG点为节点构造Lagrange插值多项式来逼近状态变量;以LG点为节点构造Lagrange插值多项式(或其他多项式)来逼近控制变量。在配点处状态变量的导数可由全局插值多项式求导来近似，从而将微分方程约束转换为一组代数约束。而性能指标中的积分项以及终端状态可由高斯求积公式计算得到。经上述离散化方法，原始最优控制问题就转化为非线性规划问题，而后通过有效的大规模稀疏NLP求解器即可求解。具体高斯伪谱法的连续最优控制问题离散化方法可参见文献［5］，在此不再赘述。

2 返回轨迹优化

2.1 动力学模型

考虑地球旋转影响，假定飞行器侧滑角为零，SLV无动力返回动力学方程［6］为:

为加快优化速度和有效地利用自动微分技术，密度ρ(r)、当地声速c(r)以及升阻力系数(CL，CD)均采用拟合模型。

2.2 状态及控制变量的选取

对于再入轨迹优化问题，最为常见的是将X=［r，θ，φ，V，γ，ψ］T∈R6作为状态变量，而 U=［α，σ］T∈R2为待优化的控制变量。这属于无惯性控制，是一种假定不存在命令延迟的理想情况。从实际系统考虑，控制舵面偏转限制必然使得攻角α、倾侧角σ存在带宽和速率限制，这在发生控制舵面故障的情况下更为明显。出于任务安全性的考虑，在模型中考虑α和σ的角速率限制。令

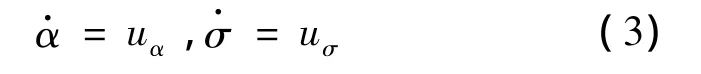
式中，uα，uσ称为“伪控制量”，作为优化时的最优控制变量，可以对其加以限制来满足实际控制能力约束。将式(1)与式(3)联立，可得新的方程及状态变量 X=［r，θ，φ，V，γ，ψ，α，σ］T∈R8，而新的控制量为U=［uα，uσ］T∈R2。

2.3 优化性能指标与各类约束

2.3.1 末端进场走廊(FAC)

目前亚轨道飞行器返回主要沿用航天飞机再入的分段策略，即再入段、末端区域能量管理段和自动着陆段，这有利于降低各段轨迹设计与制导的难度，但各段需采用不同的制导方法。对于基于最优控制理论的制导方法，只是给定期望的终端条件，寻求一条满足各种约束的最优轨迹，而能量管理、航向调整实质上是通过轨迹优化自动实现的。考虑到亚轨道飞行器返回初始高度较低，因而可以尝试合并再入段与TAEM段，从返回初始状态到自动着陆界面采用统一的轨迹优化与最优制导方法。

为了描述性能指标与终端约束，引入“末端进场走廊”(FAC)的概念［6］，如图 2所示。FAC 是在返回段终端速度、速度倾角与速度方位角、着陆场位置及方向给定情况下，能够保证飞行器安全返回的终端位置(经度、纬度、高度)的范围。FAC生成方法与具体飞行器特性、着陆场信息(如位置、跑道长度)等有关。

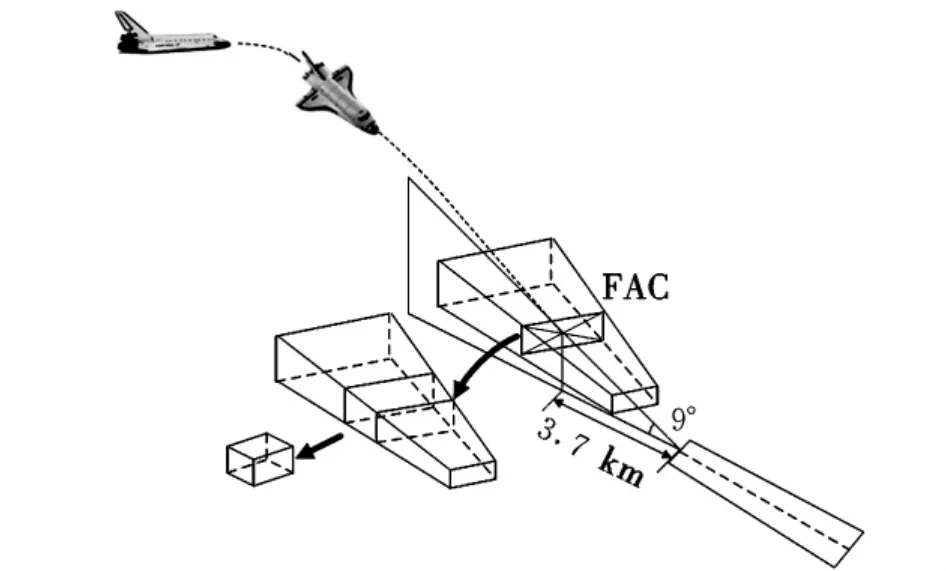
图2 末端进场走廊

2.3.2性能指标与终端约束

终端约束要求在满足其他各类约束条件下飞行器能够准确捕获FAC，即:

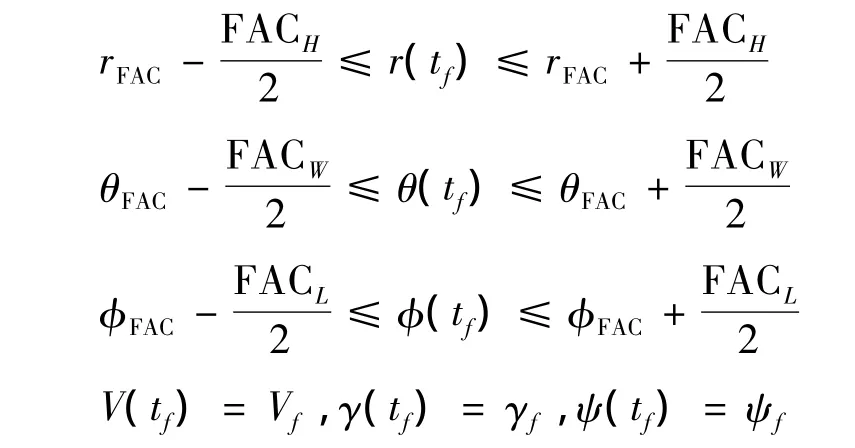
式中，rFAC，θFAC，φFAC分别为 FAC 中心的地心距、经度、纬度;FACL，FACW，FACH分别为三维 FAC的长、宽、高。

选择如下性能指标:

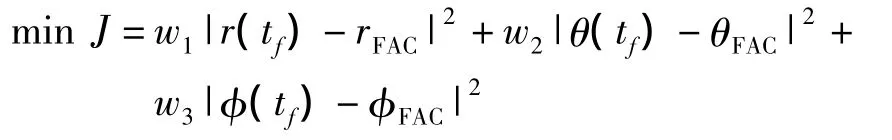
式中，w1，w2，w3为权重系数，这里选 w1=w2=w3=1，使得终端位置与末端进场走廊中心位置距离最小。

2.3.3其他约束

返回过程还需满足状态、控制量约束和过载nz、动压q、热流密度等路径约束。

3 优化算例与结果分析

3.1 优化算例

本文采用X-33总体参数及气动模型进行仿真计算［6］。

返回初始状态与终端条件约束如下:

3.2 优化结果

为便于比较，分别对不采用伪控制量和采用伪控制量两种方法进行了优化，优化结果如表1所示。

表1 优化结果比较

从表1可以看出，选用30个LG点，两种方法优化时间分别为7.240 s和9.543 s，而同样算例的文献［6］则需要25 s。本文算法在Matlab平台下实现，雅克比矩阵通过自动微分方法计算，如采用C代码、解析雅克比矩阵等手段，优化速度可进一步提高。性能指标为10－17量级，表明终端时刻飞行器非常接近FAC中心。

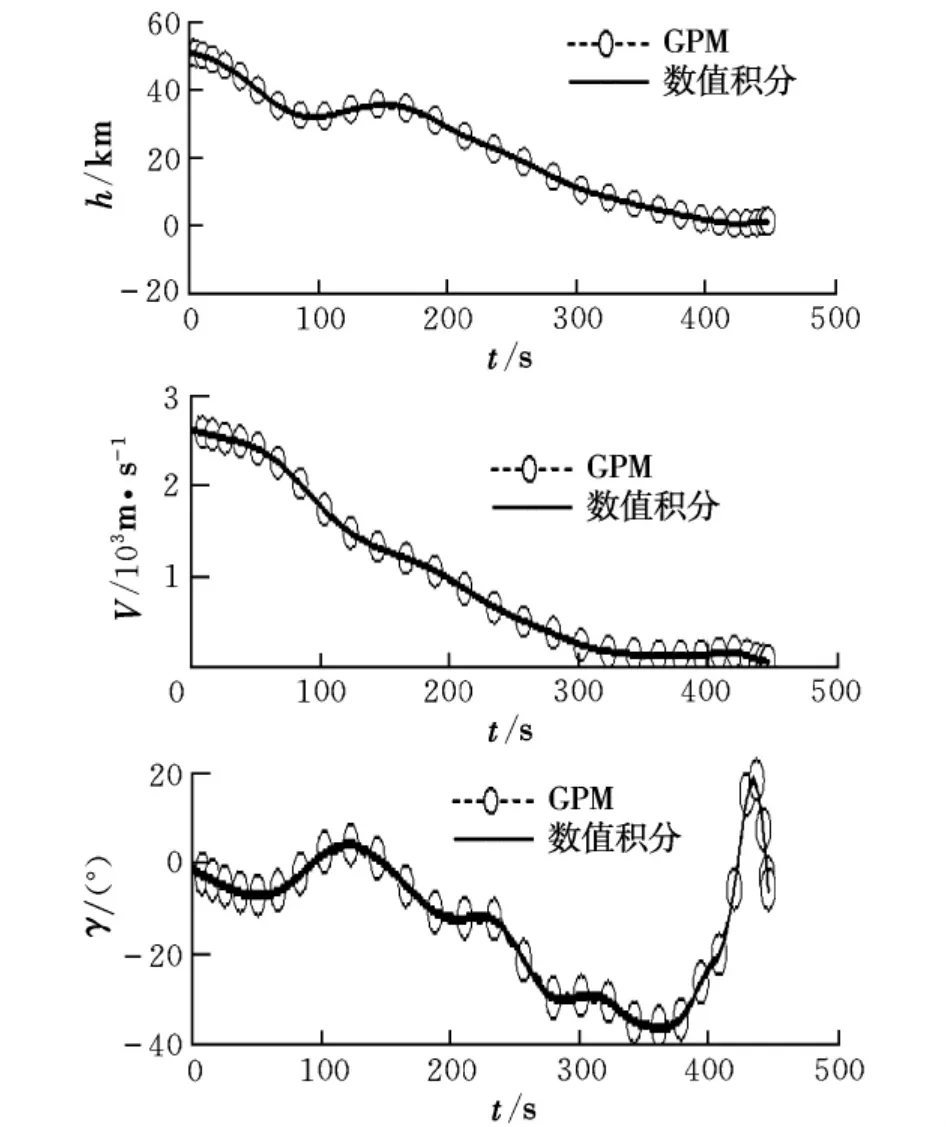
图3 状态量变化曲线

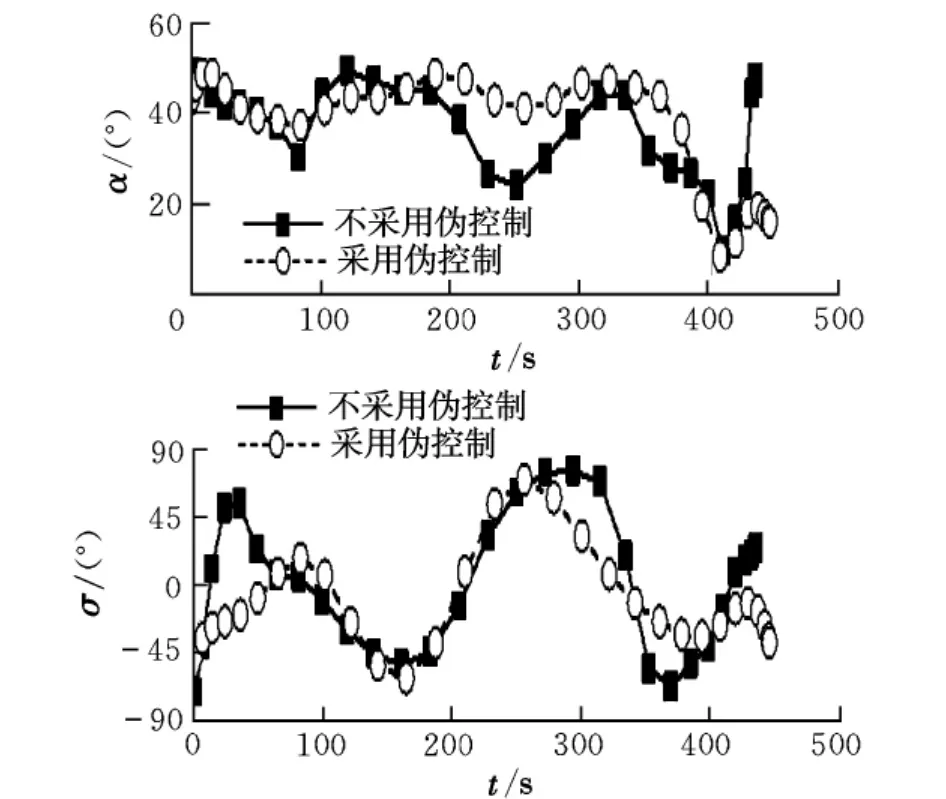
图4 控制量变化曲线

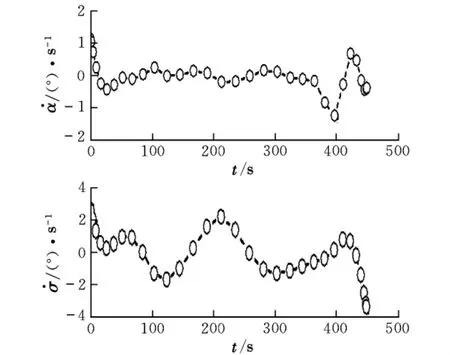
图5 伪控制量变化曲线

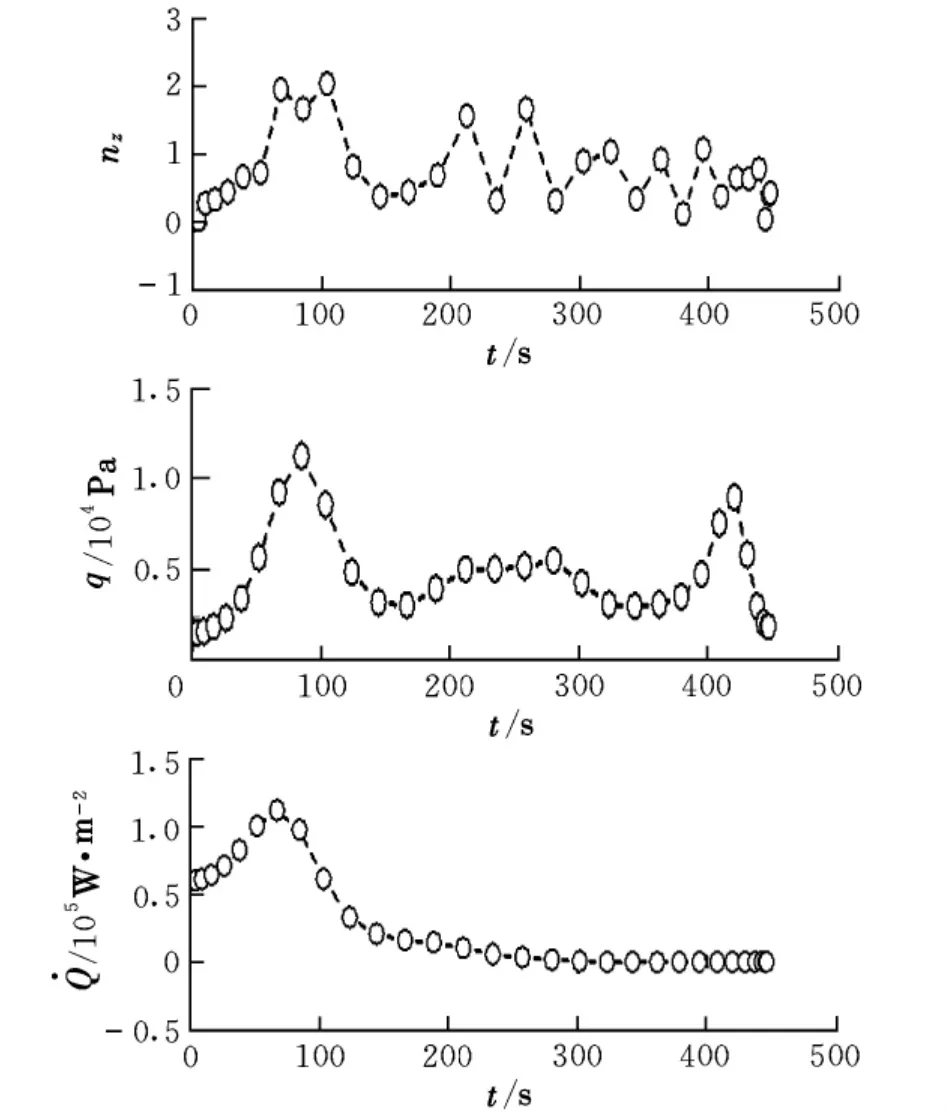
图6 路径约束变化曲线

图3～图6分别为状态量、控制量、伪控制量和路径约束变化曲线。图3中的h=r－Re表示飞行高度。从图3中可以看出，GPM优化与数值积分结果非常吻合，表明所得结果是可行的。从图4可以看出，采用伪控制量方法，攻角、倾侧角曲线更为平滑。从图5可以看出，伪控制量(即控制量攻角和侧滑角的变化率)均在要求的±5(°)/s范围内。图6表明，返回过程满足法向过载、热流密度及动压路径约束。

3.3 可行性与最优性验证

对于采用离散化方法求解连续最优控制问题而言，验证解的可行性与最优性是非常必要的。可行性通过数值积分结果与优化结果相比较来验证，积分时的控制量由最优离散控制量插值得到。GPM可以根据协态映射原理估算LG点处的协态信息，从而求得哈米尔顿函数值以检验解的最优性。本文研究对象属于存在路径约束、终端时刻自由的最优控制问题，且为自治系统，因此对应的哈密尔顿函数应恒为零，这是最优轨迹应满足的一阶最优性必要条件。

图7为Hamiltonian函数变化曲线。可以看出Hamiltonian函数接近于零，实际数据在10－11量级，可以认为所得结果接近最优解。

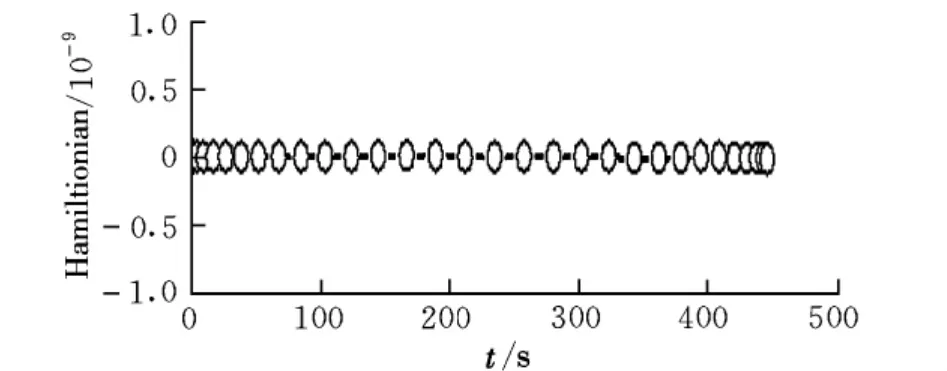
图7 Hamiltonian函数变化曲线

3.4 SLV返回三维飞行轨迹

图8为仿真得到的亚轨道飞行器三维飞行轨迹与地轨迹。

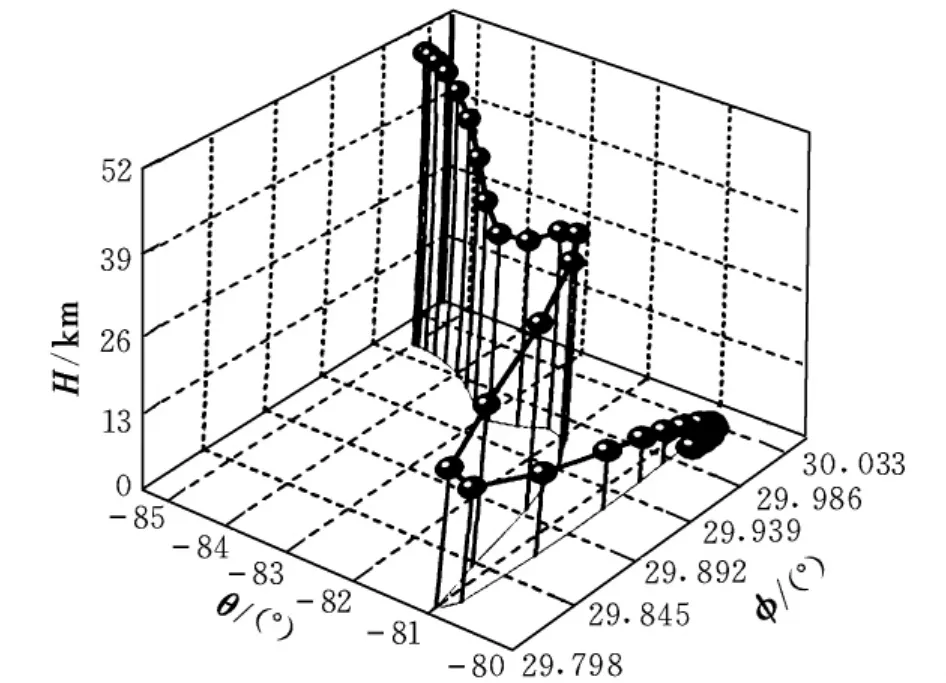
图8 三维飞行轨迹与地轨迹

尽管本文没有采用末端区域能量管理段、HAC等概念，但从图8中三维飞行轨迹可以看出，实际上全程返回段都存在能量管理机制。在返回段开始，由于能量管理能力有限，只有小的S机动;返回中段，大约从20～30 km高度开始，进行大的S转弯来消耗能量;返回末段，在小范围能量管理的同时进行航向调整。这与传统的再入分段策略大致相同，从另一个角度验证了所得结果的可行性。

4 结束语

本文利用高斯伪谱法进行了亚轨道飞行器返回轨迹优化。为增加任务安全性，在模型中考虑地球自转影响以及伪控制量约束。在描述性能指标与终端约束时，引入“末端进场走廊”概念。仿真结果表明，在满足控制能力约束、路径约束等条件下，GPM能够快速准确地生成捕获FAC中心的SLV返回轨迹。后续研究工作可考虑采用更为有效的初值猜想机制、解析雅克比矩阵等手段提高计算效率。

［1］ Mease K D，Chen D T，Teufel P，et al.Reduced-order entry trajectory planning for acceleration guidance［J］.Journal of Guidance，Control and Dynamics，2002，25(2):257-266.

［2］ Shen Z，Lu P.On-board entry trajectory planning expanded to sub-orbital flight［C］//AIAAGuidance，Navigation，and Control Conference and Exhibit.Austin，Texas，2003:1-13.

［3］ Fahroo F，Doman D B，Ngo A D.Modeling issues in footprint generation for reusable launch vehicles［C］//Proceedings of the 2003 IEEE Aerospace Conference.Big Sky，MT，2003:1-9.

［4］ Huntington G T，Benson D，Rao A V.A comparison of accuracy and computational efficiency of three pseudospectralmethods［C］//AIAA Guidance，Navigation，and Control Conference and Exhibit.Hilton Head，South Carolina，2007:1-25.

［5］ Huntington G T.Advancement and analysis of a gauss pseudo spectral transcription for optimal control problems［D］.Cambridge，MA:Massachusetts Institute of Technology，2007.

［6］ Singh B，Bhattacharya R.Optimal guidance of hypersonic vehicles using B-splines and galerkin projection［C］//AIAA Guidance，Navigation，and Control Conference and Exhibit.Honolulu，Hawaii，2008:1-11.