高超声速临近空间飞行器非开普勒轨道研究

李海林，吴德伟

(空军工程大学电讯工程学院，陕西西安 710077)

引言

临近空间是当前航空航天领域发展的研究热点，临近空间飞行器的发展对于未来空天一体化作战、防空防天反导都将产生革命性的影响［1-4］。尤其是高超声速临近空间飞行器的研究和应用，不仅是航空航天技术领域的一次飞跃，更是军事变革的尖刀。对此，国内外学者及著名研究机构纷纷投入大量科研力量，主要集中在总体设计技术、材料与热防护技术、动力装置、导航制导与控制技术和飞行轨迹等领域［5］。

临近空间介于航空领域和航天领域之间，临近空间飞行器的飞行轨迹既不像航空飞行器那样可以灵活自如地“任意”改变，也不像航天飞行器那样固定在一定轨道运行。所以，针对临近空间飞行器飞行轨迹的研究就不能简单定义为航迹规划或轨道确定。本文论述了高超声速临近空间飞行器飞行轨迹，并把非开普勒轨道的研究引入高超声速临近空间飞行器的研究范畴，从基本原理上揭示了高超声速临近空间飞行器与航空、航天飞行器的不同之处。

1 非开普勒轨道模型

航天器的开普勒轨道可由如下限制性二体问题运动方程［6］解得:

式中，r为从天体(记为m1)到航天器(m2)的位置矢量;天体引力常数μ=Gm1，G为万有引力常数，这种情况只考虑m1对m2的引力。这是一个建立在以天体质心为原点的惯性坐标系中的航天器轨道动力学方程。

相对于开普勒轨道，非开普勒轨道是指不符合开普勒三定律的天体或航天器的运行轨道，以及不符合二体问题解的天体或航天器的运行轨道。广义上定义为一切不符合理想开普勒三定律的轨道都是非开普勒轨道。但开普勒轨道和非开普勒轨道都必定符合一定的动力学原理，因为天体或航天器的运动不是无缘无故的任意行为，而是有内因或外因作用的，必有规律可寻。因此，应用牛顿力学可以导出高超声速临近空间飞行器非开普勒轨道的动力学方程［7］为:

式中，fh为作用在航天器上除天体中心引力以外的所有外力产生的加速度。式(2)与式(1)不同的是等号右边不为零，表明fh的方向与r同向，且固定不变。事实上，还有很多非开普勒轨道的fh的方向与r并不同向。

从文献［2］得出的非开普勒轨道动力学方程式(2)不具有代表性，只代表了与航天器上除天体中心引力以外的所有外力产生的加速度的方向一致的一部分开普勒轨道。由式(2)进一步推导得出更具有广泛代表性的方程如下:

式中，k为某个常系数;τd为某个力的单位矢量;rd为r的单位矢量。式(3)中fh的方向是τd和rd的矢量方向，方向并不确定。当k=1，τd和rd方向相同，式(3)与式(2)等同。

高超声速临近空间飞行器的运动轨迹遵循非开普勒轨道原理。这是由于临近空间的空气非常稀薄，万有引力定律和开普勒宇宙定律在该区域难以适用，使得遵循万有引力定律的航空飞行器不能在其中飞行，遵循开普勒宇宙定律的航天飞行器，由于受重力作用过大，难以维持其飞行轨道。因此，式(3)适用于高超声速临近空间飞行器，本文将具体论述这一观点。

2 非开普勒轨道弹跳的飞行机理

众所周知，航天器通过大气层返回地面时，再入大气层时的速度方向与当地水平线的夹角为θ，称为再入角［8］，再入角的大小直接影响到航天器在大气层里所受的气动力加热、过载和返回时的航程。以往为了使航天器能够返回地面，想尽办法控制再入角度，使其能够进入大气层安全回到地面。现在高超声速临近空间飞行器就是利用航天器返回原理的反原理进行的，亦使飞行器再入大气层时的速度方向与当地水平线相切，只能在大气层的边缘飘逸跃迁，而不进入大气层，从而保持在大气层外不断飞行。

高超声速临近空间飞行器的飞行机理如图1所示。当进入大气层时，高超声速临近空间飞行器周围的大气开始压缩，形成强大阻力，程序控制高超声速临近空间飞行器的速度V1的大小和方向，使再入角θ较小或为零。由于受大气阻力D影响，在当地水平基准的法线方向增加一个速度增量ΔV，若不考虑其他因素，根据牛顿定律，高超声速临近空间飞行器将改变原来的运动方向，朝向V1和ΔV的合成矢量方向V2运动，从而使高超声速临近空间飞行器在大气层边缘从航迹1跃迁到航迹2。

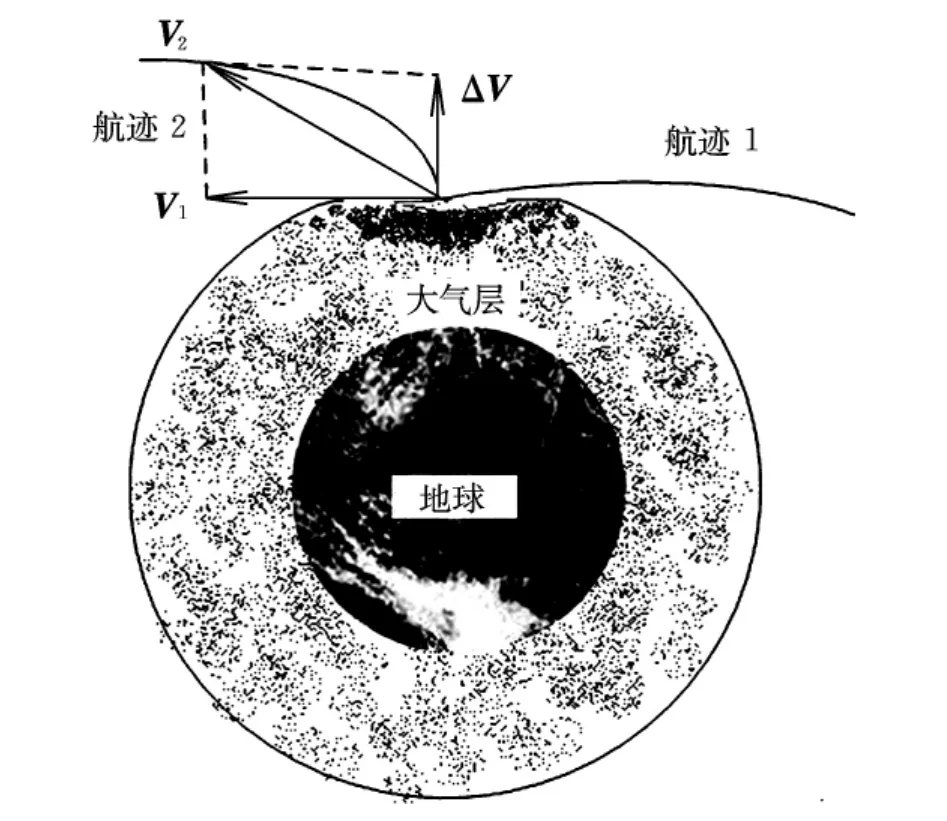
图1 飞行机理

当高超声速临近空间飞行器沿航迹2跃迁到一定距离后，受重力影响和发动机工作，程序控制高超声速临近空间飞行器再次改变运动方向，使高超声速临近空间飞行器以特定的速度朝向大气层运动，运动到大气层边缘，又会受大气阻力D影响跃迁出去。如此往复，发动机只需要适当时候进行很少工作，再加上重力的影响，就能保证高超声速临近空间飞行器在大气层边缘绕地球作弹跳式循环运动。

3 非开普勒轨道分析

3.1 巡航段非开普勒轨道动力学方程

高超声速临近空间飞行器飞行过程可分为三个阶段:发射段、巡航段和再入段。发射段的目标是将飞行器以指定的速度送入指定飞行高度，可以使用地基或天基发射方式实施。巡航段是主要的飞行阶段，飞行器在一定高度范围内进行巡航高速飞行。再入段是指飞行器改变飞行轨迹，使当地速度倾角快速变小，与大气发生碰撞，使飞行器弹跳或进入大气层对目标进行攻击。本文主要对无动力再入段进行分析。高超声速临近空间飞行器巡航段受力如图2所示。

图2 高超声速临近空间飞行器巡航段受力分析

设飞行器作角速度为ω的匀速圆周运动，FG表示法向方向的力，即地球对飞行器的万有引力，FS表示切向方向的力，即发动机推力，则飞行器的合加速度等于法向加速度加切向加速度:

由此可见，式(8)与式(3)相同，说明高超声速临近空间飞行器运行轨道是非开普勒轨道。

3.2 再入段非开普勒轨道动力学方程

实际上，飞行器在受到多个力作用的情况下，同样可以分解为以上两个方向的力。式(3)和式(8)同样适用。高超声速临近空间飞行器再入大气层时，受力情况如图3所示。图中，Cx表示气动阻力;Cy表示气动升力;FG表示地球对飞行器的万有引力;¯FS表示飞行器发动机推力。

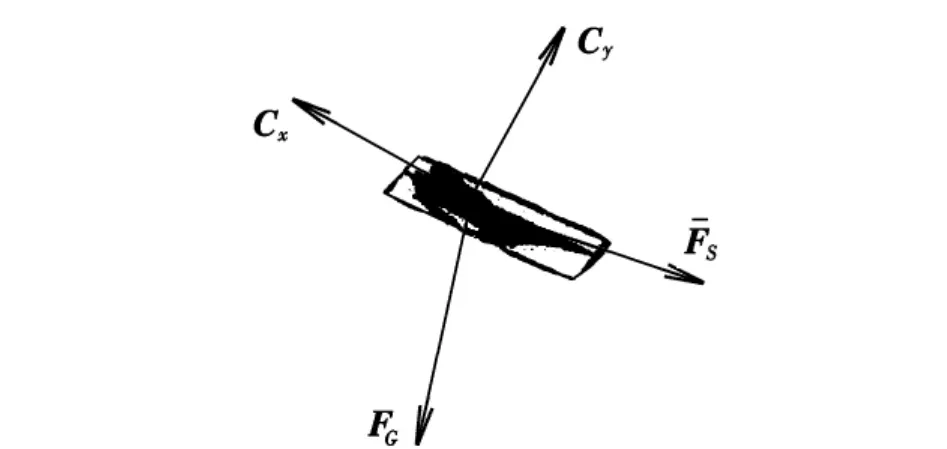
图3 高超声速临近空间飞行器再入段受力分析

由牛顿力学知识可得，高超声速临近空间飞行器所受合力FH为:

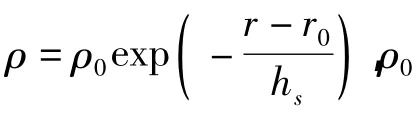
3.3 再入瞬间受力分析

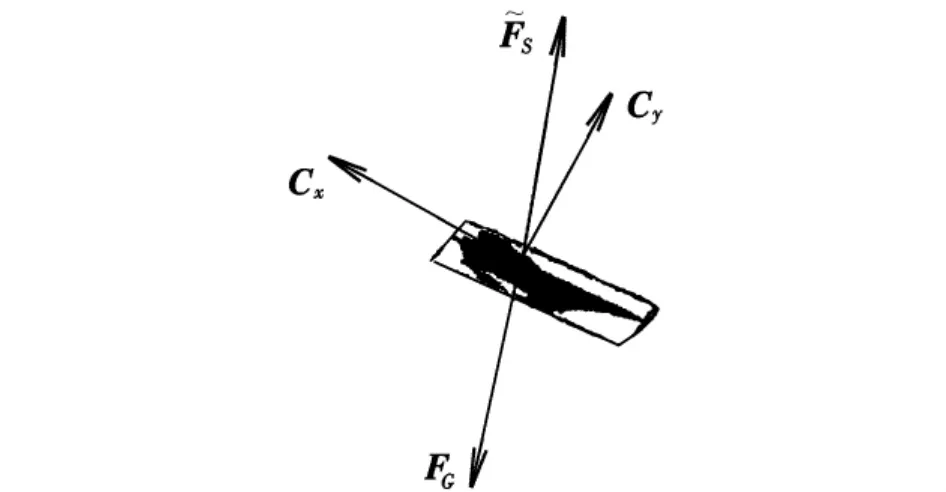
图4 再入瞬间受力分析

质点的动量表示式为:

此式只在飞行器碰撞大气层瞬间成立。

4 仿真算例与结果分析

4.1 仿真条件及参数

以高超声速再入滑翔临近空间飞行器为仿真对象，飞行器参数采用美国的空天试验机X-33的数据［9］，质量为900 kg，迎角和航迹偏航角分别为 20°和8.5°;仿真计算取再入点初始速度7 km/s，高度30 km，再入角－2°;设热流密度、动压和过载约束分别为2 000 kW/m2，500 kPa和4;要求终端高度为30 km，Ma ＞6;海平面大气密度 ρ0=1.225 kg/m3，地球质量、平均半径和自转角速度分别为5.98×1024kg，6 371.004 km 和 15(°)/h。

4.2 仿真结果及分析

经过计算，飞行器轨道变化曲线如图5所示。高超声速临近空间飞行器非开普勒轨道动力学方程求解r所得轨道曲线与文献［10］中的质心运动方程求解结果基本一致，从而说明了非开普勒轨道机动模型方程的正确性。

图5 轨道曲线

不考虑惯性的影响，把飞行器看作刚性体，再入瞬间飞行器的加速度必定在一定值以上才能保证飞行器发生弹跳，从而实现高超声速临近空间飞行器无动力非开普勒轨道弹跳式远距离常时间飞行。不考虑惯性影响飞行器的加速度曲线如图6所示。

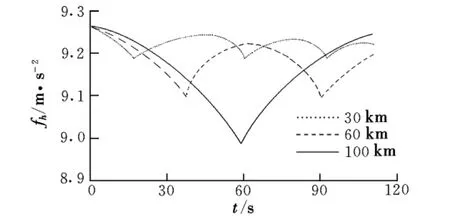
图6 飞行器加速度曲线

飞行器向下运动，加速度由大逐渐变小，当运动到高度H=100 km时为再入瞬间，必须使fh≥8.99 m/s2，λ＜1，飞行器向上弹跳运动，使加速度发生跳转，开始由小逐渐变大。飞行器向下运动，加速度由大逐渐变小，当运动到高度H=60 km时为再入瞬间，必须使fh≥9.10 m/s2，λ＜1，飞行器向上弹跳运动，使加速度发生跳转开始由小逐渐变大。飞行器向下运动，加速度由大逐渐变小，当运动到高度H=30 km时为再入瞬间，必须使fh≥9.19 m/s2，λ＜1，飞行器向上弹跳运动，使加速度发生跳转开始由小逐渐变大。

5 结束语

高超声速临近空间飞行器已经成为当今世界军事较量和科学研究的热点，涉及新材料、新飞行轨道动力学、新热防护等问题。本文着重讨论了高超声速临近空间飞行器非开普勒轨道弹跳飞行问题，并利用非开普勒动力学方程与质心运动方程进行了仿真对比，验证了非开普勒轨道动力学模型的准确性，同时仿真结果证明了该方法的可行性。

［1］ 薛永江，李体方.临近空间飞行器发展及关键技术分析［J］.飞航导弹，2011，(2):53-54.

［2］ Charles R M，Vincent LR.Preliminary X-43 flight test results［J］.Acta Astronautica，2005，57(28):266-276.

［3］ Charles R M，Vincent L R，Robert J S，et al.Hyper-X:foundation for future hypersonic launch vehicles［J］.Acta Astronautica，2005，57(28):614-622.

［4］ Mark C D，Terry W J.X-43A flight-test-determined aerodynamic force and moment characteristics at Mach 7.0［J］.Journal of Spacecraft and Rockets，2008，45(3):472-484.

［5］ 黄伟，罗世彬，王振国.临近空间高超声速飞行器关键技术及展望［J］.宇航学报，2010，31(5):1260-1265.

［6］ 肖业伦.航空航天器运动的建模［M］.北京:北京航空航天大学出版社，2003:75-76.

［7］ 陈记争，袁建平，方群.航天器在推力作用下非开普勒运动的动力学建模［C］//空间非开普勒轨道动力学与控制专题研讨会.北京:装备技术学院出版社，2008:53-54.

［8］ George H K.A navigation solution involving changes to course and speed ［J］.Navigation，1996，43(36):469-482.

［9］ Jason L S，David D，David W.Periodic optimal cruise of an atmospheric vehicle［J］.Journal of Guidance，1985，8(16):31-38.

［10］李菁菁，任章，黎科峰.高超声速飞行器再入段的动力学建模与仿真［J］.系统仿真学报，2009，21(2):534-537.