一种瞬时圆周加速度制导律设计

李伟，王志刚，蒋奇英

(1.西北工业大学航天学院，陕西 西安 710072;2.第二炮兵青州士官学校202教研室，山东 青州 262500)

引言

制导律的选择对导弹能否精确打击目标至关重要，而制导律的设计需要从导弹的飞行性能、作战空域、技术措施、制导精度、制导设备、战术使用等方面进行综合考虑与衡量［1］。

随着现代控制理论的发展，最优控制、滑模变结构控制、预测控制等诸多非线性控制方法也开始用于制导律设计，一些学者还研究了跟踪某条特殊轨迹来产生制导指令的几何曲线制导律［2］。其中最优制导律、变结构制导律、预测制导律由于制导形式过于复杂，制导参数难以选择，不适合工程运用。几何曲线制导律制导形式简单，且减少对测距信息的要求，扩展了导引头的选取范围。

针对导弹和目标速度恒定的情况，Manchester等［3-4］根据平面弹道的几何特性提出了一种具有终端角度约束的圆周制导律。其基本思想为:假定在每一时刻，导弹和目标的位置均处于同一个圆上，且所需的终端速度方向位于目标点的切线上(故每一时刻均可确定出唯一的圆)，因此只要控制导弹沿该圆飞行，即可命中目标。文献［5］中将圆周加速度概念应用到三维方案弹道跟踪，但其攻击目标是固定的，这在实际应用中存在很大弊端。

本文依照导弹质心和目标质心相对位置关系，将文献［6］中所提出的一种圆周加速度非线性制导律推广到三维情况下攻击运动目标的任务中，设计的制导律不但能够准确命中目标，而且弹道较为平直。

1 瞬时圆周加速度制导原理

介绍瞬时圆周加速度制导原理前，需要引入一个新的坐标系——相对弹道坐标系Oxryrzr。原点O选取在导弹的质心上;Oxr轴与导弹质心相对目标质心的速度矢量vr重合;Oyr轴位于包含相对速度矢量vr的铅垂平面内，且垂直于Oxr轴，向上为正;Ozr轴按右手定则确定。

制导原理如图1所示。在任一瞬时，Oxr为导弹质心相对目标质心速度矢量方向;OT为目标的质心;O1为以OOT(线段r)为弦、以Oxr为外切线的圆的圆心，其半径为R;η为垂直相对速度矢量的半径与Ozr轴的夹角，其中OO1在Oyrzr平面内;η1为弦OOT与相对速度矢量的夹角;O2为目标质心OT在Oxrzr平面内的投影，O2O3垂直于Oxr轴。

图1 瞬时圆周加速度制导原理图

2 制导方程推导

将图1中平面OO1OT取出放大后如图2所示。

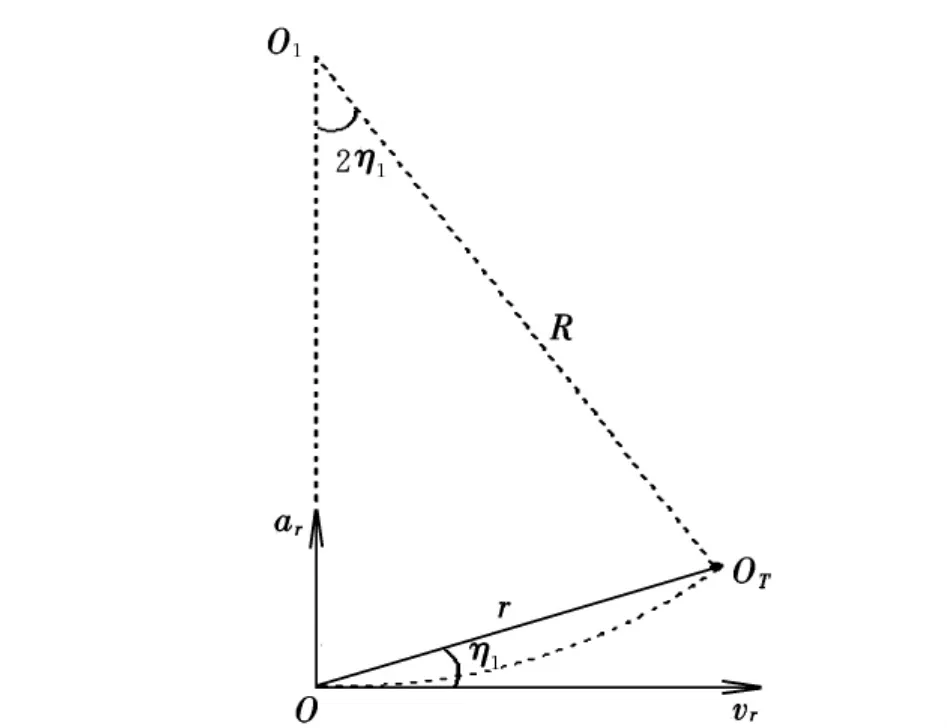
图2 制导原理的几何关系

根据图2所示几何关系，可得:

若要解算式(9)和式(10)，还需要 vr，yTr，zTr和r，其中r为弹目相对距离，可参见文献［7］通过弹目相对运动方程求解得到。

导弹质心和目标质心相对速度的大小和相对地面坐标系的方位为:

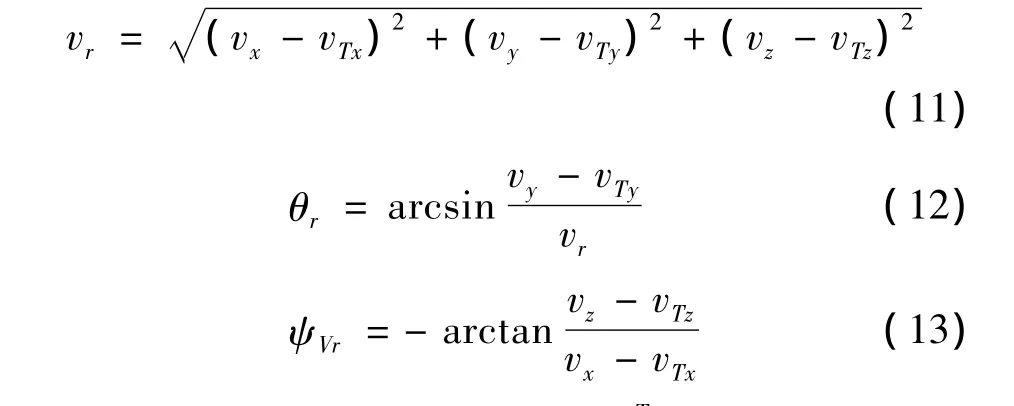
式(11)～式(13)中，［vxvyvz］T为导弹速度矢量v在地面坐标系中的分量;［vTxvTyvTz］T为目标速度矢量vT在地面坐标系中的分量。各分量的求解参见文献［7］。

导弹质心和目标质心之间的相对位置关系如图3所示。

图3 导弹和目标相对位置关系

图3中，坐标系Axyz为地面坐标系，定义见文献［7］，导弹和目标的相对距离在地面坐标系中的分量可由下式表示:

式中，qε为视线高低角;qβ为视线方位角。

弹目相对距离在相对弹道坐标系中的投影可通过地面坐标系与相对弹道坐标系之间的转换矩阵求得，即:

式中，L(θr，ψVr)为地面坐标系和相对弹道坐标系之间的转换矩阵，具体为:

参照上述公式可以求解出在相对弹道坐标系下的加速度指令，但不能直接应用在导弹动力学方程中，需要将相对弹道坐标系中的加速度指令投影至弹道坐标系中才可以使用。因此需要做两次坐标转换，首先由相对坐标系转至地面坐标系，再由地面坐标系转至弹道坐标系，即:

3 仿真计算

假设导弹空中发射攻击地面运动的武装车辆。武装车辆以匀速vT=11 m/s的速度沿着地面坐标系z轴负方向运动，武装车辆质心的起始位置坐标为xT=3 500 m，yT=1.5 m，zT=0 m。导弹仿真初始参数如表1所示，三维弹道仿真曲线如图4所示。

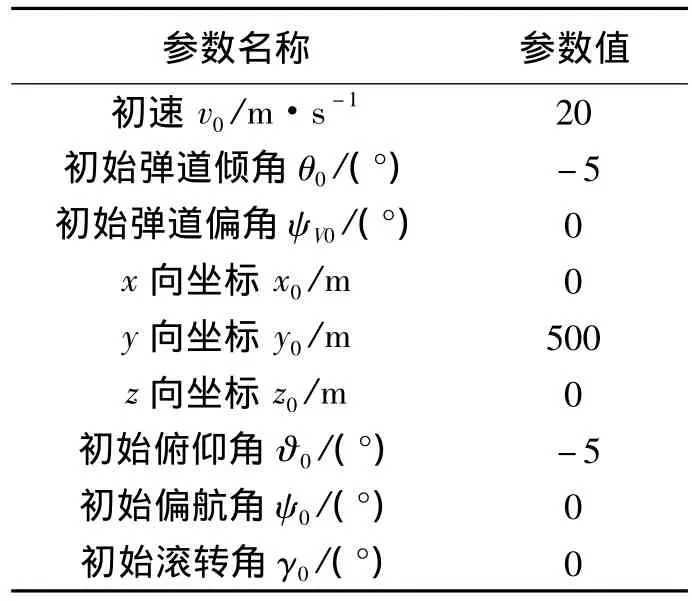
表1 导弹仿真初始参数

图4 三维弹道仿真曲线图

图5～图7给出了瞬时圆周加速度制导的弹道特性。在整个过程中，弹道角、姿态角和过载变化平滑，表明该制导方法可以得到较为平直的弹道。

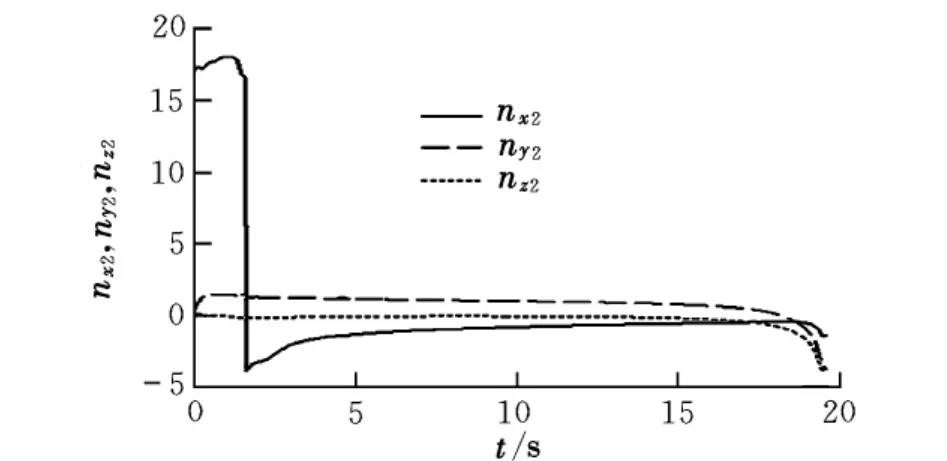
图7 过载仿真曲线

仿真结果主要参数如表2所示。

表2 仿真结果主要参数

可以看出，导弹最终命中目标，脱靶量仅为1.0 m，满足最终精确制导的要求。

4 结束语

本文介绍了瞬时圆周加速度的制导原理，并推导了制导方程。以某型导弹为例进行了弹道仿真，结果表明所设计的制导方法在攻击移动地面车辆时能够准确命中目标，而且弹道较为平直，对实际的弹目追踪问题具有一定的参考价值。

［1］ 王亚飞，方洋旺，周晓斌.比例导引律研究现状及其发展［J］.火力与指挥控制，2007，32(10):8-12.

［2］ 蔡洪，胡正东，曹渊.具有终端角度约束的导引律综述［J］.宇航学报，2010，31(2):315-323.

［3］ Manchester IR，Savkin A V.Circular navigation guidance law for precision missile/target engagement［C］//Proceedings of the 41st IEEE Conference on Decision and Control.Las Vegas，USA，2002.

［4］ Manchester IR，Savkin A V.Circular navigation missile guidance with incomplete information and uncertain autopilot model［J］.Journal of Guidance，2004，27(6):1078-1083.

［5］ 王旭刚，王中原，李小元.一种非线性方案弹道跟踪算法［J］.弹道学报，2010，22(4):23-26.

［6］ Sanghyuk P，John D，Jonathan PH.A new nonlinear guidance logic for trajectory tracking［R］.AIAA-2004-4900，2004.

［7］ 李新国，方群.有翼导弹飞行力学［M］.西安:西北工业大学出版社，2004.