飞行仿真中基于人类思维模式的飞机轨迹算法

高大鹏

（中国民用航空飞行学院计算机学院 四川 广汉 618307）

0 介绍

轨迹算法，实际上是求出在任一时刻飞机的位置，求出各个时刻的位置，就可以知道飞机的轨迹了。

在二维雷达仿真的软件中，有两种飞机轨迹算法比较常用。这两种算法实现简单，但都与实际的轨迹有较大的偏差。为了使轨迹更加接近真实和智能化，设计了一种按照人类思维模式进行建模的飞行算法。

1 常用算法介绍

1.1 飞机完全按照预设航线飞行的算法

在算法中，飞机在雷达上的轨迹与预设的航线重合，算法实现过程如下。

设飞机飞行时间为t，速度为v，则飞行距离s=tv。预设航线由一些关键点(x1,x2,… ,xn)依次用线段连接而构成。关键点存储为一个线性表l。设每个关键点的经纬度为(loi，lai)，可以得到一个递归距离序列di：

其中，dis是求两个关键点距离的函数，di为x1到xi点的距离。

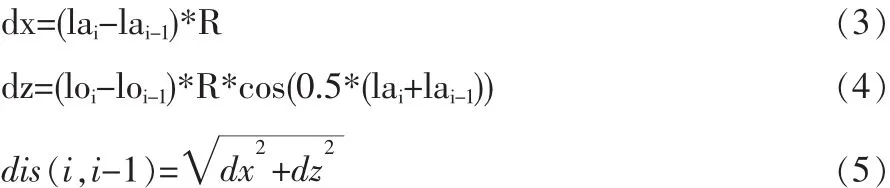
当di≤s≤di-1时，表明飞机在xi，xi-1之间，令d=dis(xi,xi-1)， d0=s-di-1，xi，xi-1的经纬度为(loi，lai)，(loi-1，lai-1)。则易得飞机的经纬度(lo，la)：

通过算法的实现，飞机严格在预设航线上移动，可以精确计算出飞机到达某一点的时间。但是飞机在转弯时违背了物理特性，没有转弯过程，转弯半径为零。

每隔3 min采集一次降雨强度、风速、覆冰重量，按时间先后顺序，分别记为P=(p(1), p(2), p(3), ……, p(10)); W=(w(1), w(2), w(3), ……,

1.2 以关键点为目标的算法

该算法描述如下：

如图1所示，p点为飞机当前位置，xi为下一个目标点，飞机飞行方向与x轴的夹角为b。p与xi的连线与x轴的夹角为a。已知当前飞机位置（lo，la）、方向heading和速度v，根据目标的位置（lo1，la1），求得下一次显示的位置、方向和速度。

首先，a和b的范围都规整为0～2π。由于民航飞机每秒转向为2°，而雷达仿真屏幕每2秒刷新一次，故可设每次转向4°。方法为：转向时，查看a-b的值，如果小于4°，则令b= a。否则，如果xi点在p点左边，则左转，令b=b＋4°，反之则右转,令b=b-4°。

得到了新的航向b后，求取下一次显示的经纬度，易得公式如下：

其中，R是地球半径。通过以上计算，可以得到飞机在任意时刻的方向和位置。算法符合物理特性，实现比较简单，但是容易发现，飞机在飞行过程中，离预设航线都有一定的距离。

图1 位置示意图

3 基于人类思维模式的轨迹算法

以上算法，都具有缺点，算法一不符合物理特性，算法二在飞行时飞机偏离航线。新算法的设计不但针对这些不足，而且是按照人类的思维模式来进行的假设。

3.1 假设

（1）为了节省燃油和时间，飞行员总是尽量选择最近的路线；

（2）为了飞行安全，飞行员总是尽量靠近预设航线；

（3）当目标点不可达时，飞行员会在遵照上两条假设的前提下，忽略目标点，前往下一个目标点；

（4）飞行员都能很好地驾驶飞机，不会出现误操作现象。

3.2 算法描述

如图2所示，飞机的轨迹一直都在预设轨道上，只有在转弯时，才偏离轨道。而且转弯半径是通过飞机的性能和速度计算出来，符合实际的飞行轨迹。

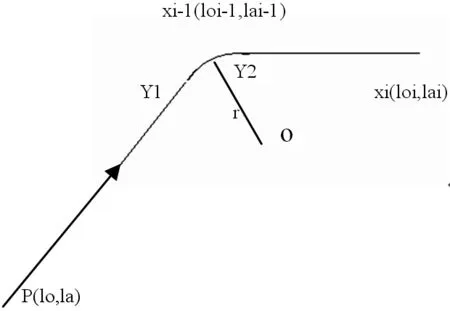
图2 飞机轨迹图

容易证明，按照这条路线，是最近的。故按照图2的轨迹飞行，满足上述假设条件。

3.3 算法实现

本算法实现简单。其本质就是计算半径为r的圆与不同夹角的外切点。

如图2所示，如果线段k1(P,xi-1)与线段k2(xi-1,xi)相交于xi-1点，设两条线段相交的夹角为2a。圆心为o，半径为r的圆，同时与k1和k2相切。得到的飞行轨迹为三个部分的连接。这三个部分为：线段(P,Y1)，圆弧(Y1,Y2)，线段(Y2,xi)。故只需求出Y1和Y2的坐标即可。

根据平面几何知识，易得到Y1，Y2的坐标。

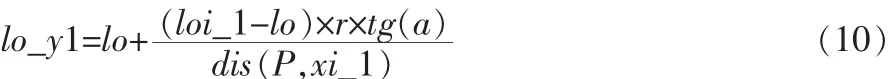
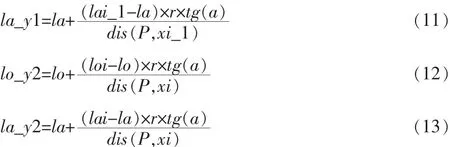
（10）到（13）式中，Y1的经纬度为(lo_y1，la_y1)，Y2的经纬度为(lo_y2，la_y2)。式中其它变量与图2中对应。Dis函数由（5）式说明。

至此，算法得到了完整的飞行轨迹。下图3为程序截图。

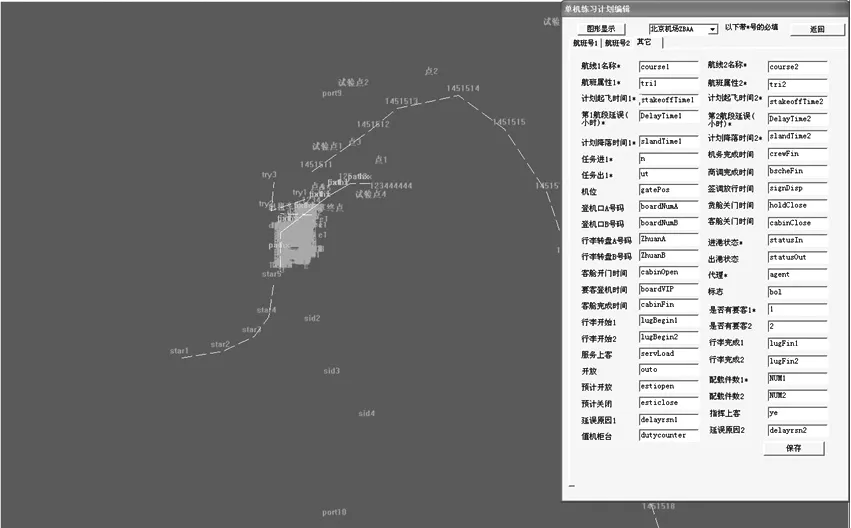
图3 程序运行截图

4 结论与未来的工作

飞行仿真是一个严肃的工作，仿真的真实程度对飞行员和航空管制员的训练效果直接相关。飞行仿真越真实，训练效果就越好。

所以在实现仿真过程中，应尽量使实验效果贴近现实。

采用本文提出的方法，飞行轨迹与现实中的飞机飞行轨迹最为接近，可以达到更好的仿真效果。

［1］骆慈孟.空域、飞行程序与机场建设[J].空中交通管理，1995，2.

［2］蔡东闽.空域评估系统及其仿真研究[D].南京航空航天大学，2002.

［3］卢敏.基于GIS飞行程序的设计[D].北方工业大学，2006.

［4］中国民用航空总局第191号令.CCAR-140民用机场运行安全管理规定[S].2007.