钢丝绳约束加固砖砌体短柱轴压性能的有限元分析

张建波

（同济大学土木工程学院 中国 上海 200092）

0 引言

纤维复合材料(FRP)加固砌体结构和混凝土结构是近年来蓬勃发展的一种新型加固方式。它以其优异的材料性能，方便快捷的施工方式，良好的加固效果而越来越受到人们的关注。但其本身存在的两个重要问题需要考虑，首先是粘结剂的耐高温性能不足，需要切实的防火措施；其次，FRP与其它加固材料相比要更加昂贵。而钢丝绳约束加固砌体柱的方法不仅保留了纤维加固的优点，且避免了纤维加固的两个不足，有望在加固工程中得到应用（图1）。然后，目前关于钢丝绳约束加固砌体柱的研究很少。本文通过Ansys有限元模拟，对钢丝绳约束加固砌体柱短柱的轴压性能作初步分析。

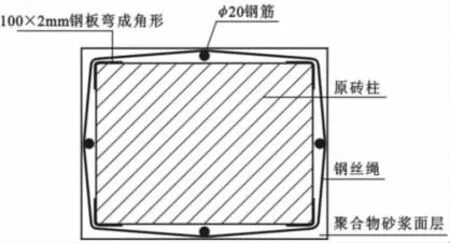
图1 钢丝绳约束加固方法示意图

1 有限元模型

1.1 单元选择

砌体是由砌块和砂浆组成的二相复合材料，对其进行有限元分析常有两类模型：分离模型和均质化模型。分离模型即是将砌块和砂浆分别建模，可采用两种处理方式：一种是不考虑砖与砂浆之间的粘结滑移，将砌块与砂浆接触面的所有节点自由度耦合在一起；另一种是考虑砖与砂浆之间的粘结滑移，将砌块与砂浆通过接触单元或非线性弹簧单元联系在一起。由于本文的主要目的是研究砌体柱承载力提高幅度与钢丝绳加固量的关系，故选择较为方便的均质化模型。

根据国内外学者对砌体结构有限元分析的成果[1][2]，本文采用SOLID65单元模拟砌体，采用LINK8单元模拟钢丝绳，采用SHELL41单元模拟FRP布，采用SOLID45单元模拟刚性垫板。

1.2 本构关系和破坏准则

当采用CONCRETE材料时，可结合多线性随动强化模型（MKIN）或多线性等向强化模型（MISO）来定义砌体的单轴应力应变曲线。砌体的破坏准则采用William-Warnke五参数模型，SOLID65将破坏分成四种情况，即通过主应力状态确定为四个区域，在不同的区域采用不同的破坏准则。在压-压-压区域，采用William-Warnke五参数破坏准则，如满足破坏准则，则砌体被压碎；在拉-压-压区域，基本采用William-Warnke破坏准则，如满足破坏准则，则砌体在垂直于主拉应力的平面发生开裂；在拉-拉-压区域，不再采用William-Warnke破坏准则，极限抗拉强度随主压应力绝对值的增大而降低，如满足破坏条件，在垂直于拉应力的方向上产生开裂；在拉-拉-拉区域，应力超过砌体极限抗拉强度就发生开裂，也即在垂直拉应力的方向上都可能发生开裂[3]。笔者研究后发现，由于多线性随动强化模型（MKIN）或多线性等向强化模型（MISO）都采用了Von Mises屈服准则，而Von Mises屈服准则不能反映静水压力的影响，最后导致有限元分析结果比试验结果小很多。

基于上述原因，本文采用了Drucker-Prager(DP)屈服准则，该屈服准则是修正的莫尔-库伦准则，改进了Von Mises准则与静水压力无关的缺点。文献 [4、5]采用DP模型对AFRP约束混凝土短柱进行了有限元分析，计算结果与试验符合较好。Ansys中DP模型的定义需输入的三个参数，即粘聚力c、内摩擦角φ和膨胀角φf，一般由试验确定或根据经验选取。

1.3 实体建模与求解设置

为了提高计算效率，本文按对称简化建了1/4模型，模型的尺寸按试验尺寸确定，为了避免应力集中的影响，模型作了倒角处理。本文不考虑砌体与钢丝绳或FRP之间的粘结滑移，两者共用节点。为了保证计算的收敛，一般建议砌体单元的边长不小于50mm[1]。由于本文试件的尺寸较小，为了保证计算的精度，取砌体单元的边长为10mm左右。为避免加载时产生应力集中，在柱的两端设置了刚性垫块。本文采用位移加载，力收敛准则。求解算法采用Newton-Raphson迭代法，子步数取为300，为加速计算，开启自动时间步，最大平衡迭代次数取为50，收敛精度取0.01，采用残余力的二范数控制收敛。有限元模型见图2。

图2 有限元模型

2 有限元的计算结果及分析

2.1 有限元模型的验证

为了验证有限元模型的可靠性，本文先对文献[6]中的几个FRP约束矩形砌体柱进行了模拟。试件编号为FN-A-RX，其中F表示纤维布类型 （C表示CFRP，G表示GFRP），N表示FRP层数，A表示截面的长宽比，X表示倒角半径。例如C3-1-R10表示采用3层CFRP包裹的截面长宽比为1的矩形砌体短柱，倒角半径为10mm。有限元计算结果与试验结果的对比见图3，可以看到竖向平均应力-平均应变曲线与试验基本吻合，DP模型可以很好地模拟强约束下砌体的受力性能。本次DP模型的参数取为：粘聚力c=3MPa、内摩擦角φ= 24度、膨胀角φf=5度。因此，采取DP模型模拟钢丝绳强约束砌体短柱的轴压性能是可行的。

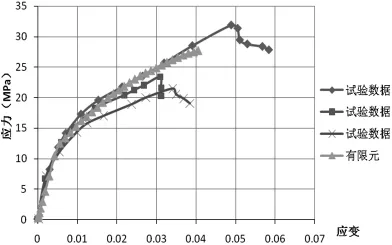
图3 C3-1-R10应力-应变曲线对比

2.2 钢丝绳约束矩形砌体短柱的有限元计算结果

有限元模型中，砌体柱的尺寸和材料属性同C3-1-R10，钢丝绳采用6×7+IWS型的不锈钢丝绳，公称直径4.0mm，有效截面面积为7.45mm2，弹性模量为105000MPa，绕绳间距为6.9mm。钢丝绳约束矩形砌体短柱的轴向平均应力-平均应变曲线如图4所示，可以看出明显的双线性特征。砌体柱中部截面的横向应力分布如图5所示。可以看到矩形截面边长中点附近的约束力较小；截面角部和中心的约束应力较大。砌体柱的竖向应力分布如图6所示，可以看到截面角部和中部的应力较大，这是由于中部和角部的横向约束应力较大所致。

图4 钢丝绳约束矩形砌体短柱在轴压下的平均应力-平均应变曲线

3 结论

通过对钢丝绳约束加固砖砌体短柱的数值模拟，对其轴压性能有了初步的认识，可以得到以下结论：

3.1 与FRP约束砌体柱一样，钢丝绳约束加固砌体柱可以有效地提高其轴压强度，达到预定的加固效果。强约束下，钢丝绳约束加固砌体柱的轴向应力-应变曲线呈现明显的双线性特征。

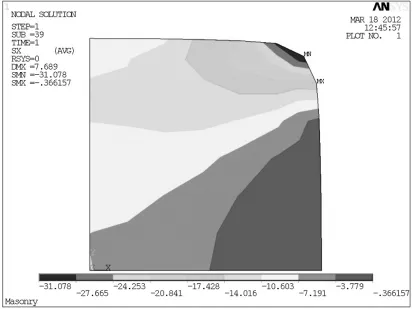
图5 砌体短柱中部截面x向应力分布图

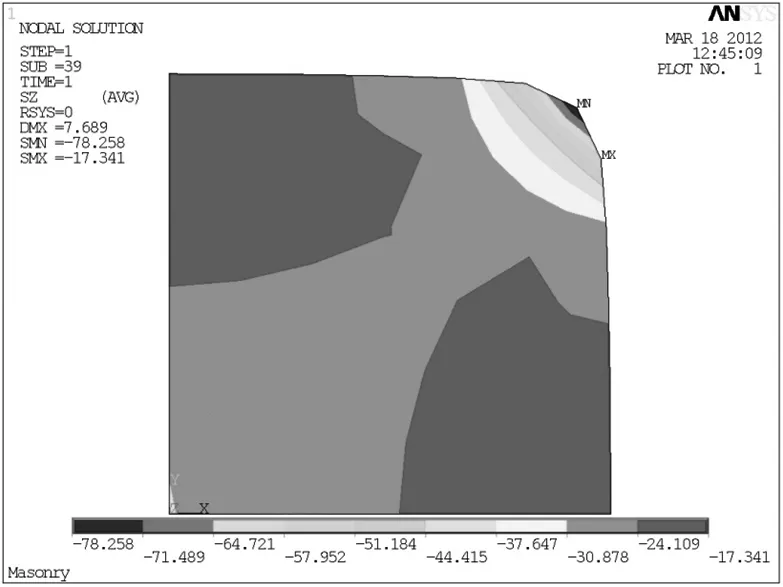
图6 砌体短柱中部截面的竖向应力分布云图

3.2 通过Ansys有限元分析与试验数据的比较，表明Ansys有限元可以很好地模拟钢丝绳约束加固砌体短柱的轴向受力全过程。

3.3 钢丝绳对矩形截面的约束是不均匀的，在角部较大，在截面边长中点附近较小。且其约束应力分布与截面的倒角半径有密切关系，所以可以通过增大倒角半径的方法来增强约束效果。

［1］李英民，韩军，刘立平.ANSYS在砌体结构非线性有限元分析中的应用研究[J].重庆建筑大学学报，2006，28(5)：90-96.

［2］陆新征，冯鹏，叶列平.FRP布约束混凝土方柱轴心受压性能的有限元分析[J].土木工程学报，2003，36(2)：46-51.

［3］王新敏.ANSYS工程结构数值分析[M].北京∶人民交通出版社,2007.

［4］Amir Mirmiran,Kenneth Zagers,Wenqing Yuan.Nonlinear finite element modeling of concrete confined by fiber composites[J].Finite Elements in Analysis and Design,2000(35)∶79-96.

［5］王元丰.AFRP约束混凝土柱性能理论[M].北京∶科学出版社，2011.

［6］Theofanis D.Krevaikas, Thanasis C.Triantafillou. Masonry Confinement with Fiber-Reinforced Polymers[J].Journal of Composites for Construction,2005,9(2)∶128-135.