液压挖掘机回转传动机构-工作装置的系统动态方程

李兆军，毛 涛，刘小苏，梁光辉

(广西大学机械工程学院，广西 南 宁 530004)

回转传动机构和工作装置，是液压挖掘机的重要组成部分，它们在液压挖掘机回转和作业过程中，起着非常大的作用[1]。其动态性能的好坏，不仅直接影响整台机器的正常工作，而且还直接关系到操作人员和设备的安全，因而其动态性能是整机设计水平的重要标志。深入研究回转传动机构和工作装置的动态性能，对液压挖掘机使用和整机的设计具有十分重要的意义。

近年来，人们不仅对液压挖掘机回转传动机构动力学问题进行了大量的研究[2~3]，而且在液压挖掘机工作装置动力学问题的研究，也取得了许多令人欣慰的成果[4~6]。但是，液压挖掘机回转传动机构和工作装置，不是孤立存在的，而是一个相互作用、相互影响的耦合系统，因而有必要将液压挖掘机的回转传动机构和工作装置，作为一个系统对其动力学问题进行深入研究。然而，迄今未见有综合研究液压挖掘机回转传动机构-工作装置系统耦合动力学问题的文献。

本文以液压挖掘机回转传动机构-工作装置系统为研究对象，运用有限元法建立液压挖掘机回转传动机构-工作装置系统动态方程，并通过实例对系统的动态响应进行分析。

1 回转传动机构动力学方程

在一般的分析中，通常把齿轮视为刚体，实际上齿轮是一个弹性体，在运转过程中，齿轮的啮合会产生振动。简单而不失一般性，在液压挖掘机回转齿轮传动机构动力分析中，进行如下简化：在内齿轮与行星齿轮啮合工作中，忽略因回转轴承受到倾覆力时两个齿轮回转轴的变化；行星齿轮通过其回转轴与挖掘机转台刚性连接，即忽略齿轮回转轴和挖掘机转台的弹性变形。

由于液压挖掘机工作过程中，回转传动机构的内齿轮固定在底架上，假设内齿轮为静止不动，则只有行星齿轮绕回转中心轴公转。

如图1所示，坐标系XOZ为液压挖掘机回转齿轮传动机构单元坐标系(Y方向为垂直于纸面向内)。由于动力学分析中主要考虑轮齿的弹性变形，则回转传动机构在Y轴方向上的纵向位移为零。设u11为内齿轮轮齿绕Y轴的转角位移；u12为行星齿轮绕其自转轴的转角位移；u13、u14分别为行星齿轮轮齿在XOZ平面内的横向位移，将这两个位移在1点出表示出来。于是，此液压挖掘机回转传动机构的广义坐标列阵可表示为u1={u11u12u13u14}T。

图1 齿轮转子的力学模型

1.1 回转传动机构的动能

根据动能定理，液压挖掘机回转传动机构系统的动能可表示为

m1为行星齿轮的质量；

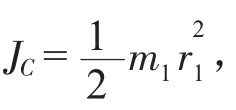
Jyy为工作装置和转台上其他构件的转动惯量，Jyy=J'+Jy，其中J'为转台上其他构件的转动惯量。

对于液压挖掘机回转传动机构，简单而不失一般性，只考虑啮合齿轮XOZ平面内的横向位移，不考虑行星齿轮回转驱动轴的弹性变形；在行星齿轮运动的绝对速度的计算中，由于齿轮驱动速度较低，弹性体的弹性位移比较小，故不考虑运动中的刚体运动与弹性运动的耦合项[7]。则行星齿轮运动的绝对速度可表示为

φ觶r为行星齿轮绕Y轴的角速度；

θ觶r为行星齿轮绕其自转轴的角速度；

r2为内齿轮的基圆半径。

将式（2）代入式（1）得

1.2 回转传动机构的势能

回转传动机构是由行星齿轮和内齿轮组成，回转传动机构系统的势能即为行星齿轮和内齿轮之间轮齿啮合的弹性势能，可表示为[8]

式中，

kf为行星齿轮与内齿轮间的啮合刚度；

δ为行星齿轮与内齿轮的作用线上的弹性变形量，可表示为

其中，

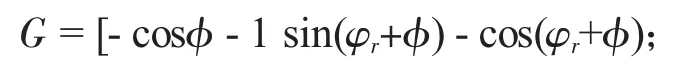
准为齿轮啮合的压力角。

由于齿轮在啮合过程中，齿轮的啮合刚度kf具有明显的周期性，因而啮合刚度kf的傅立叶级数形式可表示为[9]

式中，

km为平均啮合刚度，

kn为第n阶谐波的幅值，

ωe为齿轮副的啮合频率，

准1n为相位角。

将式(5)代入式(4)，整理得

式中，回转齿轮传动机构系统的刚度矩阵可表示为

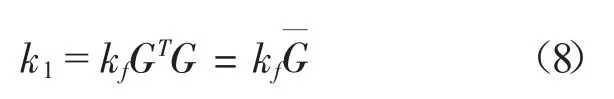
将式(6)代入式(8)，得

1.3 回转传动机构动力学方程

根据拉格朗日方程原理，液压挖掘机回转传动机构动力学方程可写为

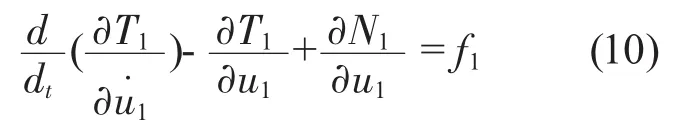
式中，

f1为外加载荷的广义力列阵。

将式（3）和式（7）代入式(10)中，经整理，得到液压挖掘机回转传动机构系统在不考虑阻尼情况下的运动微分方程为

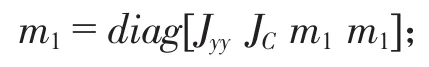
将式(9)代入式(11)，得

2 变截面梁单元动力学方程

为了更加全面分析液压挖掘机工作装置的动态特性，这里应用有限元法对工作装置进行动态特性分析。由于液压挖掘机工作装置各构件的长径比较大，可以用梁单元对工作装置各构件进行模拟，而且工作装置构件的横截面的宽和高都是变化的，故采用变截面梁单元对其进行模拟计算。由于宽度的变化率较小，故忽略宽度的变化。为了简便而不失一般性，在液压挖掘机工作装置机构动力分析中，进行如下简化：

在研究工作装置机构梁单元上任一点的绝对加速度时，忽略加速度和速度中的弹性变形运动与刚体运动的耦合项；忽略梁弯曲时梁的截面沿轴向的微小位移；在应变能计算中，忽略剪切变形的影响以及横向位移对拉压应变能的影响。此时，变截面梁单元动力学方程可表示为[10]

式中，

m02为变截面梁单元质量矩阵；

k02为变截面梁单元刚度矩阵；

f02为变截面梁单元外加载荷广义力列阵。

3 系统动态方程

液压挖掘机回转传动机构-工作装置系统，是由回转机构单元和变截面梁单元组成，将回转机构单元和变截面梁单元的运动微分方程组装起来，即可得到回转传动机构-工作装置系统的运动微分方程。

为简便而不失一般性，这里对系统进行做如下简化：

回转传动机构与工作装置通过转台刚性连接，即不考虑转台的弹性变形。

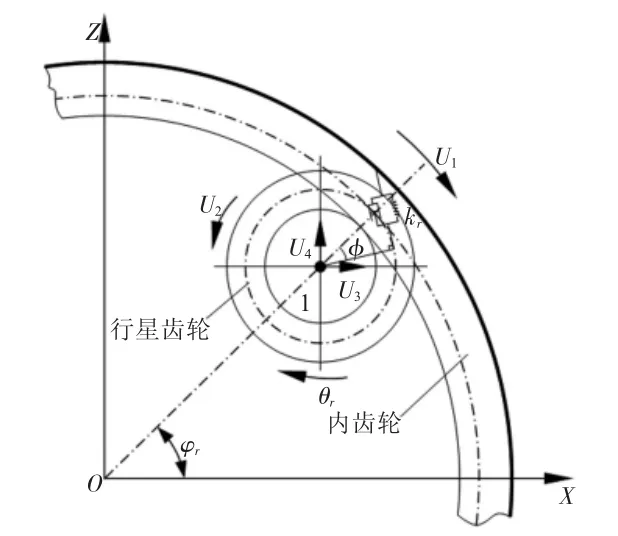
图2 齿轮转子有限元分析简图

图3 工作装置有限元分析简图

在对系统进行有限元分析时，将回转传动机构和斗杆各作为1个单元，将工作装置分为3个单元，如图2、图3所示。

图中 1、2、3、4、5 为节点编号，①、②、③、④为单元编号，共设置了 19 个广义坐标，分别用 U1、U2、U3、…、U19表示，

其中 U3、U4、U6、U7、U8、U11、U12、U13、U16、U17、U18为弹性位移；

U1、U2、U5、U9、U10、U14、U15、U19为平面内的弹性转角，则系统的广义坐标列阵可表示为

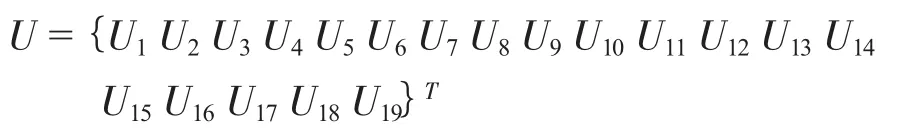
设第i单元坐标与整体坐标间的转换矩阵为Ri，第i单元局部编号与系统编号间的坐标协调矩阵为Bi，利用对应的转换矩阵和协调矩阵，则可将回转传动机构动力学方程与变截面梁单元动力学方程组装起来，得到计入阻尼影响的液压挖掘机回转传动机构-工作装置系统动态方程为

C为采用粘滞阻尼理论近似估计得到的系统阻尼矩阵，且

其中，

mi为第i单元的质量矩阵；

ki（i=2,3,4）为第i单元的刚度矩阵；

fi为第i单元的广义力列阵。

由于液压挖掘机工作装置与回转传动机构，通过刚性体连接在一起，回转传动机构对工作装置的振动有着直接的影响，而工作装置的振动也直接影响到回转传动机构的动态特性，也就是说，液压挖掘机回转传动机构-工作装置系统内部存在着复杂的耦合关系，而这种复杂的耦合关系，能由式(14)中较好地反映出来。

4 实例分析

本节以由三一重工生产的SY65C-9小型液压挖掘机为求解对象，其回转传动机构的齿轮参数如表1所示，其工作装置各构件为箱型结构，其几何尺寸如表2所示（表2中参数名见图3），且回转传动机构副啮合频率ωe=86.67Hz。

由于液压挖掘机回转传动机构-工作装置系统的动态特性，随着系统的位姿不同而不同。这里讨论两种位姿下的动态性能。

位姿一：β1=60°，且 β2和 β3分别在极小值的位置；

位姿二：β1=30°，且 β2和 β3分别在极大值的位置。

β1、β2和 β3如图3所示。

表1 回转齿轮几何参数

表2 工作装置各构件的几何尺寸

表3所示为系统在两种位姿下的前三阶固有频率的值，显然，位姿二时系统的固有频率，比位姿一时系统相对应的固有频率要大，这是因为位姿二时工作装置的等效转动惯量，小于位姿一时工作装置的等效转动惯量，从而导致的缘故位姿二时系统的固有频率，要大于位姿一时系统相对应的固有频率。

表3 系统前三阶固有频率

图4、图5分别为两种位姿下的回转齿轮啮合点的动态响应仿真图。显然，图4所示的时域响应曲线的幅值，要大于图5所示的相应幅值，这是因为系统在位姿一时，其自激惯量力要比系统在位姿二时的自激惯量力大，从而导致系统的动态响应的幅值也较大的缘故。

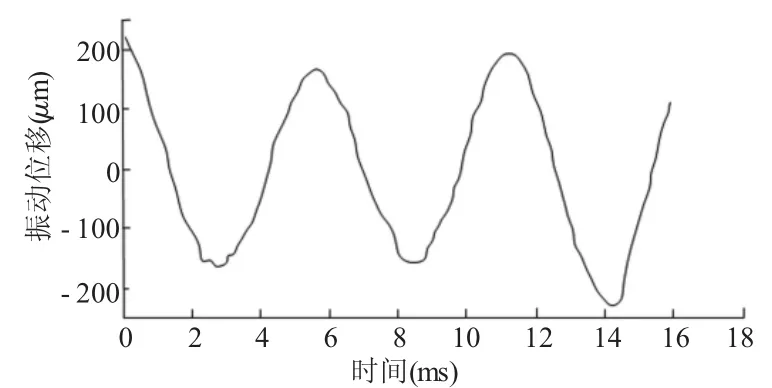
图4 Z方向时域响应仿真曲线图(位姿一)

图5 Z方向时域响应仿真曲线图(位姿二)

5 结束语

液压挖掘机回转传动机构和工作装置，是一个相互作用、相互影响的耦合系统，因而有必要将液压挖掘机的回转传动机构和工作装置作为一个系统，对其动力学问题进行深入研究。

本文以液压挖掘机回转传动机构-工作装置系统为研究对象，应用有限元法建立了液压挖掘机回转传动机构-工作装置系统的耦合动力学模型。

所建方程较好地体现了该系统动态性能与其结构参数、运动参数之间的内在关系，表达了以往方程未能反映的动态性能，为进一步深入研究液压挖掘机回转传动机构-工作装置系统的动力学特性与系统的结构参数及运动参数之间的内在联系奠定了基础。

[1]刘建新，张志勇.PC650-5型挖掘机回转机构损坏原因分析[J].工程机械与维修，2002，（6）:113.

[2]陆军坊，柯 坚，邓 斌，等.小型液压挖掘机回转齿轮的建模与动力学仿真[J].制造业信息化，2007，（11）:71-73.

[3]Junli Y,David J E,Peter E D L.A computational intelligent fuzzy modelapproach for excavator cycle time simulation[J].Automation in Construction,2003,12(6):725-735.

[4]Bartelmus W,ZimrozR.Vibration condition monitoringofplanetary gearbox under varying external load[J].Mechanical Systems and SignalProcessing,2009,23(1):246-257.

[5]郭立新，王守春，郑春歧，等.液压反铲挖掘机工作装置有限元动态分析[J].中国机械工程，2000，11(12):1338-1340.

[6]刘鹏虎，张 勇，张 强.液压挖掘机工作装置的动力学分析及控制[J].中国工程机械学报，2007，5(1):72-74.

[7]Wszolek G.Vibration analysis of the excavator model in GRAFSIMprogram on the basis ofa block diagram method[C].Journal ofMaterialProcessingTechnology，2004，(157-158):268-273.

[8]FrimpongS,Li Y.Virtual prototype simulation ofhydraulic shovel kinematics for spatial characterization in surface mining operations[J].International Journal ofSurface mining,Reclamation and Environment,2005,19(4):238-250.

[9]张 策.弹性连杆机构的分析与设计[M].北京:机械工业出版社，1997.

[10]王建宏.风力发电机的柔性多体动力学研究[D].重庆:重庆大学，2009.

[11]宋少芳.齿轮副非线性动力学模型的建立与分析[D].长春：吉林大学，2007.