基于仿真的粘滞阻尼系数对刚体接触力影响的分析

纪宁毅，李 虎

（中国船级社质量认证南京分公司，江苏 南 京 2 10011）

美国MSC公司的仿真分析软件ADAMS，是著名的机械系统动力学仿真分析软件。在ADAMS软件中，尽管可以定义多种二维或者三维的接触关系，但是求解的准确性往往让人不是很满意。究其原因，笔者认为是在运用该软件仿真分析与处理问题过程中的参数设置不当造成的。本文基于粘滞阻尼理论对机械系统动力学仿真分析软件ADAMS中的机构系统多接触参数设置问题，作一些初步研究与探讨。

1 ADAMS中多接触求解的问题

由于ADAMS对多接触问题的求解稳定性并不是太高，导致了该软件对多接触问题的求解条件要求比较苛刻。笔者经过长时间的摸索发现，在模型简化、约束添加、仿真步长与求解器选择均符合仿真分析要求的前提下，依据模型材料特性和几何特性，对多接触仿真分析参数的选取，将决定了多接触问题的求解结果正确与否。机构的多接触仿真参数选取得不当，仿真结果将受影响，甚至在某些严重的情况下，会造成接触体间相互穿透，如同没有定义接触。

2 粘滞阻尼

在机械系统中，粘滞阻尼是最常用的一种阻尼模型，系统通过把构件间的碰撞接触力，定义成一种非线性的弹簧阻尼系统模型进行计算，即接触力由两部分组成：非线性弹簧单元和线性阻尼单元。发生接触碰撞的构件材料等效刚度，当作弹簧单元的刚度，阻尼单元用于计算能量的损失[3]。

碰撞接触力的表达式为[1]

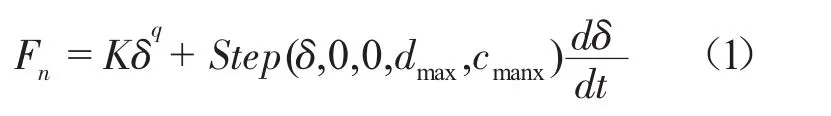
对于式（1）中的非线性弹簧部分Kδq，可由Hertz碰撞模型直接获得[7]，即

其中，

K为接触体的等效刚度，取决于接触物体的材料和结构形状；

δ为瞬态切肤深度；

q为幂指数；

E为等效弹性模量；

E1和E2分别是两物体材料的弹性模量；

R为接触体的等效曲率半径；

R1和R2分别是两物体接触处的当量曲率半径；

μ1和μ2分别为两物体的泊松比。

机械系统中的绝大部分接触碰撞，并非是相对静止不动的，而是属于动态的接触碰撞，接触体相互靠近的距离是个变量，同时考虑到能量的守恒与损耗，在非线性弹簧部分后加入阻尼项c*dδ/dt，形成一个非线性的弹簧阻尼系统，则

为了避免求解函数变量在接触瞬间，由于阶跃突变而引起的不连续，系统把阻尼系数c定义成一个step函数，即

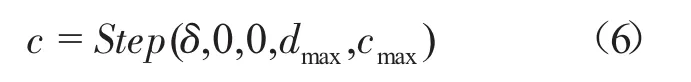
将式（6）带入式（5），即可得到碰撞接触力的表达式（1）。

式（6）中，

dmax为最大切肤深度；

cmax为最大阻尼系数。

dmax的作用，在于定义系统的阻尼何时达到最大值。

当两物体接触后的瞬态接触切肤深度δ≥dmax时，阻尼系统中阻尼系数的取值为cmax；

当0≤δ＜dmax时，阻尼系统中的阻尼系数由step函数决定，其大小与切肤深度的关系变化如图1所示。

step函数是一个3次多项式，当瞬态接触切肤深度δ=0时，阻尼系数c=0；

当 δ=dmax时，c=cmax，然后保持不变。

Lankarani和Nikravesh曾提出确定式(1)中阻尼单元的最大阻尼系数cmax的方法[8]：

式(7)中ζ被称为滞后阻尼因子，而且

式（8）中的等效刚度 K 可由式（2）获得，δ觶(-)是两物体碰撞前在接触点公法线方向的相对速度，即

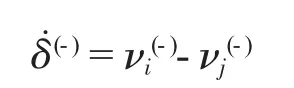
νi(-)和νj(-)分别为两物体碰撞前碰撞点的速度在接触点公法线方向的投影，e为恢复系数，它表示物体在碰撞后速度恢复程度，也表示物体变形恢复的程度，并且反映了两个物体在碰撞过程中机械能损失的程度。

由式（8）可知，滞后阻尼因子ζ不仅与碰撞实验测得的恢复系数e和碰撞前物体接触点公法线方向的相对速度δ觶(-)有关，同时也与等效刚度K有关。所以，最大阻尼系数cmax不仅与两碰撞物体本身材料属性（杨氏模量、泊松比等）有关，同时也与两碰撞物体的几何特性及运动特性有关。

3 仿真实例分析

为了能够更形象直观地阐述在多接触仿真分析过程中最大阻尼系数对仿真结果的影响，本文特选取两种典型的多接触模型加以举例分析说明。该模型分别如图2、图3所示。

图1 球碰撞板

图2 斜齿轮接触模型

图1为一球体从具有一定高度的位置自由落体与放置在地面的长形板体发生碰撞；图2为一对斜齿轮的多接触啮合模型，该模型为了实现齿轮传动，须通过齿轮间的接触来完成。在分析过程中，为了避免施加的负载发生突变，负载转矩的定义使用step函数平缓施加。模型间的接触定义为实体与实体（Solid-Solid）接触。

在机械系统动力学仿真分析软件ADAMS中，完成对图1中模型的约束和载荷的添加，以及求解器的设置和仿真控制。在最大阻尼系数cmax的取值分别为0N·s/mm、0.005N·s/mm、0.02N·s/mm和0.1N·s/mm，而其他接触碰撞参数

K=5e+4 N/mm3/2，q=1.5，dmax=0.01 mm，

接触中不考虑摩擦。

图3表示了球体质心与板体质心的位移变化曲线，图4表示了球体与板体碰撞的接触力变化曲线图。

图3 球体质心与板体质心的位移变化曲线

图4 球体与板体碰撞的接触力变化曲线

从图3和图4仿真曲线变化图可知，在最大阻尼系数cmax=0 N·s/mm时，球体的质心位移和碰撞接触力均是周期性变化，球体与板体发生了完全弹性碰撞，机械能守恒。在最大阻尼系数cmax的取值分别为0.005 N·s/mm、0.02 N·s/mm和 0.1 N·s/mm时，球体的质心位移和接触力，不仅随着撞击次数的增多而逐渐衰减，并且最大阻尼系数cmax的取值变化情况，决定了碰撞过程中机械能的衰减速度与程度。

对于图2的一对斜齿轮啮合传动，在其余约束定义准确的前提下，将斜齿轮的啮合定义成实体与实体的接触碰撞。小齿轮（主动轮）转动周期是1 s。图5表示了当最大阻尼系cmax分别取50 N·s/mm、5 N·s/mm、0.5 N·s/mm和0 N·s/mm时，而其他接触参数

K=8.97e+5 N/mm3/2，q=1.5，dmax=0.01 mm，

同时接触中考虑摩擦力，静摩擦系数μs=0.08，动摩擦系数μd=0.05，静滑移速度νs=0.1 mm/s，动滑移速度νd=10 mm/s，并且保持不变的情况下，斜齿轮接触啮合力的变化曲线图。

图5 斜齿轮啮合接触力变化曲线

从图5仿真结果可以看出：在最大阻尼系数cmax=50 N·s/mm时，齿轮间的啮合接触力在仿真时间达到4.76 s时放生了穿透现象，其余时刻基本趋于平稳，接触力可以正常准确的计算，当cmax分别取5 N·s/mm、0.5 N·s/mm和 0 N·s/mm时，齿轮刚开始接触传动的一段时间内，都可以顺利计算，但是随着时间的增加，接触力会发生跳跃，波动明显产生，模型接触穿透加剧，函数的求解过程中发生多次发散不收敛，数值不准确。从上图还可以看出，当最大阻尼系数的数值从大到小的变化过程中，接触力发生波动穿透的时刻随之提前，并且波动穿透会加剧。

4 结束语

本文在理论与实践结合的基础上，分析了在多接触求解问题过程中参数的设置，指出最大阻尼系数cmax的不同取值，对系统的多接触仿真分析结果的影响。从实践中可知，cmax数值的选取，直接决定了接触过程能量的损失程度与求解结果的准确性，从而体现了该参数在接触碰撞求解过程中的重要性。本文可为多接触问题的研究提供了一些理论基础与实践经验，同时对多接触的进一步研究，具有一定的参考与借鉴作用。

[1]陈立平，等．机械系统动力学分析及ADAMS应用教程[M]．北京：清华大学出版社，2005．

[2]石明全．基于ADAMS的多接触问题研究[J]．计算机工程与应用，2004，（29）：220-222．

[3]洪 峰.时滞阻尼理论[J].世界地震工程，2001，17(3)：1-8.

[4]李 斌，陶皎皎，赵 雷．桥梁结构的阻尼理论及其在ANSYS 中的实现[J]．四川建筑，2007，27（4）：117-118．

[5]Johnson K L．Contact Mechanics[M]．Cambridge：Cambridge University Press，1985．