分离变量法在解方程中的应用
2012-02-23李先记
李先记
(河南化工职业学院,河南 郑州 450072)
分离变量法是把含各个变量的项分离开来,从而将原方程拆分成多个更简单的只含一个未知量的方程,这种数学方法在解方程时的应用非常广泛,既可以用这种方法解代数方程,也可以解微分方程中的常微分方程和偏微分方程.
1 代数方程
分离变量法解代数方程,适用的范围相对而言要小一点,只有当一个多元代数方程f(x1,x2,……,xn)=0 中的 f(x1,x2,……,xn)可以转化为

其中f1(x1)≥0;f2(x2)≥0;……;fn(xn)≥0时可以对原方程进行变量分离:
由于 f1(x1)≥0,f2(x2)≥0,……,fn(xn)≥0,当 f(x1,x2,……,xn)可以转化为 f1(x1)+f2(x2)+……+fn(xn)=0时原方程成立当且仅当f1(x1)=0;f2(x2)=0;
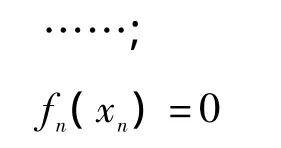
成立,所以方程f(x1,x2,……,xn)=0就可以化为n个一元方程联立而成的方程组然后解方程组即可.

2 常微分方程
2.1 分离变量法还可以用来解一类常微分方程以及通过换元法(即凑微分法)可转化为通过分离变量法能进行变量分离的微分方程.用分离变量法能解常微分方程的方程类型为:

解这类微分方程就是分别把关于x,y的表达式写在等号的两边,这样可以将两个变量x,y分离到方程的两边,然后方程两边分别求其不定积分,就可以得到常微分方程的通解.分离变量法解微分方程的具体步骤如下:

第三步,求出不定积分,得到微分方程的通解.
实例1 1838年荷兰数学家韦尔侯斯特(Verhulst)提出的一个自然环境条件所能容许的最大人口数Nm的人口预测模型,即Logistic人口模型:

是一个可以用变量分离法求解的一阶常微分方程,具体解法是:

2.2 利用换元法可化为能用变量分离法解的常微分方程
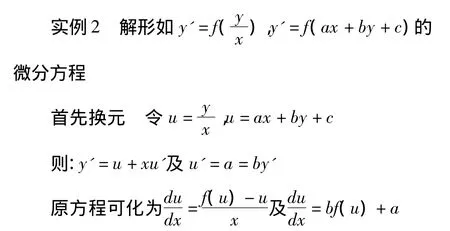
上述两个微分方程可以利用变量分离法求出其通解,然后回代,即可求出原微分方程的通解.
2.3 凑微分法和分项组合法可化为能用变量分离法解的常微分方程
实例3 解形如xy′+y=f(x)g(xy)的微分方程
注意到方程的左边即为(xy)′,可设u=xy代入原方程得

此方程也可以用变量分离法求出其通解,然后通过u=xy求出y,即求出原微分方程的通解.
3 偏微分方程
给一个关于n元函数 f(x1,x2,……,xn)的偏微分方程,有时候为了将问题的偏微分方程化为一组常微分方程,我们可以猜想解的函数的表达式为

实例4 假若关于函数F(x,y,z)的偏微分方程为


其中,c1,c2,c3都是常数,且 c1+c2+c3=0.
偏微分方程的通解为
F(x,y,z)=c1x+c2y+c3z;其中,c1,c2,c3是常数.而上述方程的两边乘以sin2θ,然后再移项可得

此方程的左边只与θ有关而与φ无关,而右边只与φ有关而与θ无关,故实际左、右两边与θ、φ都无关应为一常量,设此常量为λ(λ≥0),同样可以进行变量分离,变量分离后得

则通过应用两次变量分离,得到三个微分方程,这三个方程分别为

这三个方程分别只含有一个自变量了,各自均为常微分方程了,可将其中的偏导之符号∂改为一元函数的导数符号“d”了,这三个方程,分别称为R(r)方程、Θ(θ)方程和 Φ(φ)方程,这三个方程的常微分方程的表示形式为

且均为2阶的常微分方程,第一、第二个两个二阶的常微分方程可以先用换元,再用级数法来解,这里不再详细叙述.第三个二阶的常微分方程是一个常系数的二阶线性齐次微分方程,解法相对简单,可通过先求出其特征方程,求出特征方程的特征根,再写出微分方程的通解.
通过上面的叙述,可以说分离变量法是把含有多个变量的方程化为求单个变量的方程的一种重要的数学方法,这种方法特别在解数学物理方程中的偏微分方程的作用更加突出.
[1]南京工学院数学教研组.数学物理方程与特殊函数(第2版)[M].北京:高等教育出版社,1982.
[2]郝金库,王万得.化学生物数学简明教程[M].北京:国防工业出版社,2003.
[3]孙书安等.高等数学[M].北京:气象出版社,1998.
[4]戎笑,于德明.高职数学建模竞赛培训教程[M].北京:清华大学出版社,2010.
