微电机电刷用蜗卷弹簧的优化设计

2012-02-22赵先锋史红艳

微特电机 2012年7期

赵先锋，史红艳，何林

(1.贵州大学，贵州贵阳550025;2.国家精密微特电机工程技术研究中心，贵州贵阳550008)

0 引言

蜗卷弹簧因为维护简单、防潮、防爆广泛应用于计时仪器和时控装置［1］。在微型电机中，常把蜗卷弹簧作为电刷的能量源，压迫电刷与高速转动的换向器保持接触状态。由于工作时蜗卷弹簧始终处于压缩储能状态，在重复的扭转过程中会引起疲劳断裂，因此，蜗卷弹簧的受力分析对其在使用中的可靠性极其重要。目前关于蜗卷弹簧受力问题的研究论文还比较少。陈楠等利用圆渐开线作为弹簧的型线，利用有限元方法分析了其刚度变化［2］;傅吉龙等利用Ansys分析了蜗卷弹簧的最大等效应力，并进行了疲劳分析［3］。现有的文献研究主要集中在蜗卷弹簧的刚度分析和疲劳分析两方面，没有对蜗卷弹簧的可靠性做进一步分析，也没有提出相应的结构设计优化方案。

为了对蜗卷弹簧进行结构优化设计，提高其可靠性，本文针对某微型电机电刷所使用的蜗卷弹簧分析其压缩过程，得出应力分布和变形规律，在此基础之上，以降低蜗卷弹簧的最大应力为目标，通过改变设计参数，进行对比分析，得出优化方案，提高蜗卷弹簧的可靠性。因为蜗卷弹簧扭转过程是一个高度非线性过程，既有绕轴向的转动和弯曲，也有簧片接触后的相对滑动，理论上的简化计算不能反映其扭转过程的复杂境况，因而借助有限元方法对这个过程进行分析，考察其应力分布和层间相对滑动。

1 几何建模

平面蜗卷曲线的数学表达是阿基米德螺旋线，其直角坐标方程：

式中：ρ=aθ+ρ0;a为单位角度在矢径上的增量，a;θ为转角;ρ0为起始矢径;ρn为结束矢径;n为圈数。

在微型电机中，其空间有限，故各部件尺寸紧凑，本文使用的阿基米德螺旋线的参数分别为ρ0=1.5 mm，ρn=3 mm，n=4，可知 a=1.04 ×10-3mm。

使用SolidWorks建立蜗卷弹簧的三维模型的方法如下：首先，利用式(1)计算阿基米德螺旋线的多个离散点，赋值给样条曲线函数，绘制阿基米德螺旋线;然后，在样条曲线函数的基础上，给起始点矢径值增加一个壁厚量，利用同样的方法，绘制其另一条阿基米德螺旋线;最后，使用直线封闭螺旋线的两个端点，形成闭合曲线，完成蜗卷弹簧的平面图，如图1所示。考虑到蜗卷弹簧在工作过程中，其他零件对它的受力会产生影响，为保证分析结果的准确性，将其放入工作系统中进行分析，建立了蜗卷弹簧的装配系统，其装配的三维模型如图2所示。

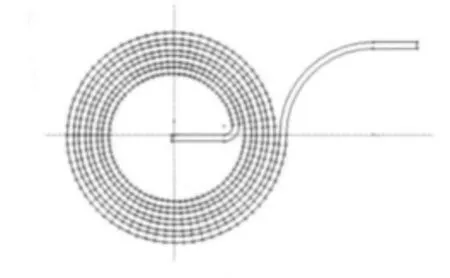
图1 蜗卷弹簧平面图

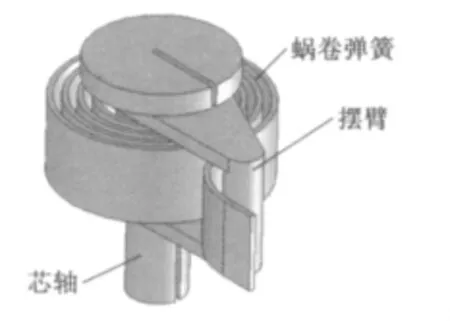
图2 蜗卷弹簧装配图

2 材料特性与边界条件

蜗卷弹簧工作系统由弹簧、芯轴和摆臂三部分组成，这三个组成部分所采用的材料及其物理参数，如表1所示。

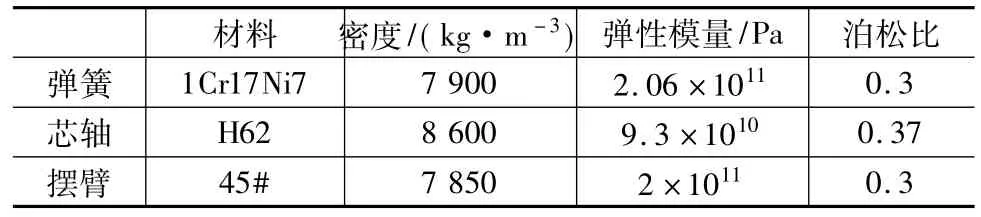
表1 材料物理参数

蜗卷弹簧系统工作的过程：当摆臂绕轴转动时，接触到蜗卷弹簧的表面，带动蜗卷弹簧扭转，能量被积累在蜗卷弹簧中。蜗卷弹簧扭转过程既有绕轴向的转动和弯曲，也有簧片接触后的相对滑动。因此，在进行边界条件设置时，将芯轴表面和蜗卷弹簧的表面、蜗卷弹簧的内外表面(自接触)、蜗卷弹簧的内表面和轴的外表面均设为摩擦接触状态，滑动摩擦系数为0.1。为考察蜗卷弹簧的受力情况，给摆臂施加一个刚体位移，在一个时间单位内，绕轴转动135°(保证弹簧转动125°)。

网格是影响分析结果准确性的一个重要因素。对零件的网格划分采用六面体网格，簧片为主要分析对象，故将其网格划分得较细，其他两个零件划分的单元网格尺寸稍大，整个模型共划分8 257个单元，如图3所示。

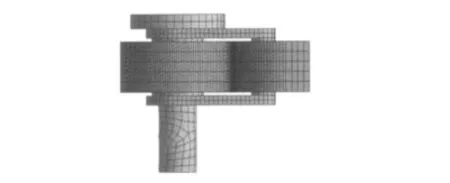
图3 蜗卷弹簧有限元模型

3 数值计算结果与分析

根据蜗卷弹簧的工作和受力特点，从簧片转动位移、簧片间的相对滑动和簧片上的应力分布三个方面来分析蜗卷弹簧的扭转过程和受力分布情况。

3.1 簧片转动位移

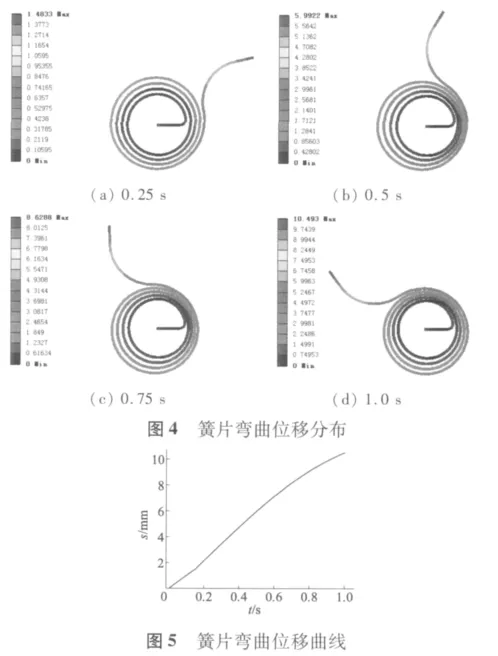
对于簧片的位移情况，取 0.25 s、0.50 s、0.75 s、1.0 s四个时间步的平面位移进行分析，其结果如图4所示。由图4可知：当摆臂接触到簧片，簧片随摆臂转动，簧片由外层向内层弯曲，簧片间隙变小，对面簧片间的间隙变大，外面两层簧片接触后，外层簧片传递力到第二层簧片，第二层簧片与第三层簧片间间隙变小，对面二、三层簧片的间隙变大，随着摆臂的转动，簧片接触依次向内层传递。簧片末端最大位移随时间的变化曲线如图5所示。因簧片间的间隙、簧片自身的弹性和簧片间的相对滑动，簧片末端位移是一条非线性曲线，随时间先凹后凸。

3.2 簧片层间的相对滑动

簧片层间由外圈向内圈依次接触，接触位置随转动方向移动，同时伴随着邻圈簧片间的相对滑动，在0.3 s前最大相对滑动位置在簧片与摆臂的接触处，簧片间尚未发生接触。在0.3 s后最大滑动位移发生在最外圈簧片和相邻簧片间，其最大值为0.998 61 mm，相邻簧片间的滑动位移由外层向内层依次递减，在1 s时摆臂转动到最大位置，最内圈簧片与相邻簧片之间尚未接触，无相对滑动。最大滑动位移曲线如图6所示，图中有两段不同斜率的直线，斜率较小的直线描述了摆臂与簧片从开始接触到相对稳定的过程中的相对滑动，从0.3 s后，外层簧片与内层簧片开始接触，其相对滑动随摆臂的转动而变大，其斜率远大于前一段直线的斜率。

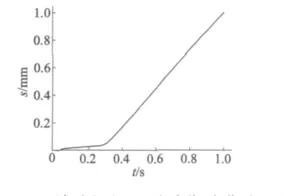
图6 簧片间相对滑动位移曲线

3.3 簧片上的应力分布

在转动过程中，簧片弯曲应力变化的大小及位置是影响簧片寿命的主要因素。在整个摆臂转动过程中，相邻簧片间接触的部位不是应力最大值处，应力最大值位置在发生变化，其变化趋势：随摆臂的转动绕轴心转动;同时由外圈向内圈移动;和摆臂成对角关系，相比接触位置滞后一定的角度。摆臂到达最大值时，簧片的应力最大值处在最内圈的应力集中处，即圆周簧片与横向簧片过渡连接处，此处是簧片最易失效或断裂的地方。值得注意的是当最大转动角度变化时，圆周簧片与横向簧片过渡连接处不一定是应力最大处。计算结果显示簧片最大的应力值为983.18 MPa，簧片的设计最大应力为1 580 MPa，可以看出簧片的最大应力小于其设计极限。簧片随时间的弯曲过程最大应力变化曲线如图7所示，最大应力曲线是随时间波动的一条曲线，每相邻层簧片接触时都会引起应力曲线斜率的的变化。

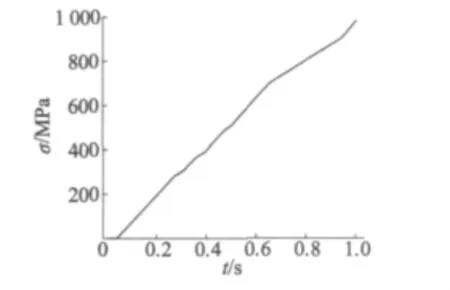
图7 簧片弯曲过程应力曲线

4 结构优化

提高簧片的寿命和可靠性的方法是：在不改变簧片外形尺寸和装配空间的前提下，降低簧片的最大应力。通过数值分析发现，在所给条件下扭转过程中最大应力的位置出现在螺旋簧片和横向簧片过渡连接处。因此，针对最大应力位置，考虑两个主要参数对其进行优化分析：(1)过渡圆弧的半径;(2)弹簧圈数。

因装配空间所限，簧片的过渡圆弧变化不能太大，否则簧片与芯轴在过渡圆弧处会发生干涉;其他参数不变，通过减小簧片间的间隙来增加簧片的圈数。改变上述两个参数，通过数值计算，得出了改变两个参数对应的最大应力，如表2所示。从表2中可以看出，簧片的最大Von Mises应力随着圆弧半径的增大而有微弱减小，随着弹簧圈数的增加而迅速下降。

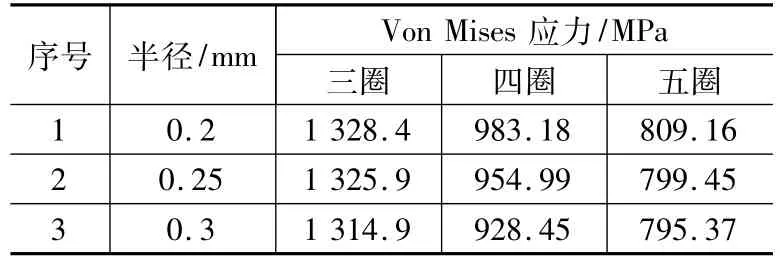
表2 蜗卷弹簧的最大Von Mises应力

在未优化之前，簧片4圈，过渡圆弧 r=0.2 mm，增大簧片过渡圆弧半径(0.2 mm变为0.3 mm)，同时增加一圈簧片(4圈变为5圈)时，弹簧的Von Mises应力有较大下降，由原来的983.18 MPa降低为 795.37 MPa，降低了 187.81 MPa，其值只有设计要求(1 580 MPa)的一半，其安全系数由1.6提高到2.0。可见，该优化方案大幅提高了产品的寿命和可靠性。