爆炸近区流场的数值模拟方法研究
2012-02-22徐春光白晓征刘瑜刘君
徐春光,白晓征,刘瑜,刘君
(1.国防科学技术大学 航天与材料工程学院,湖南 长沙410073;2.中国人民解放军总参谋部 陆航研究所,北京101121;3.大连理工大学 航空航天学院,辽宁 大连116024)
0 引言
凝聚态炸药爆轰及其与空气的相互作用问题具有广泛的应用背景,相应的实验及理论研究已经有了上百年的历史,例如对于常见的球形装药空中爆炸问题,目前已经积累了大量的实验数据及经验公式,理论研究也相对完善。对于结构所受爆炸波的冲击载荷,相关研究也很丰富[1-2]。但是实验研究具有成本高、危险性大的缺点,而数值模拟具有低成本、低危险性、高效率的优点,而且能够模拟无法进行实验,或者实际中极少出现的故障情况,近年来随着数值模拟技术的发展,数值模拟受到了越来越多的重视,在实验设计、实验结果推广、故障诊断、工程实际等方面都得到了越来越多的应用。
数值模拟爆炸波的远场效应时,可不考虑爆轰反应的细节而采用瞬时爆轰模型,认为炸药爆轰瞬时完成,形成一团高温、高压的均匀燃气;也可采用点爆炸模型或者经验公式给出计算的初场,这些方法在爆炸波与物体相互作用的模拟方面都取得了很好的效果[3-4]。如果爆炸初场的半径取得较大,则爆轰产物密度较小,可用完全气体状态方程来描述,这样将进一步降低数值计算的难度。
但当模拟爆炸近区的流场时,尤其当此流场与爆轰波发展过程密切相关时,就必须同时模拟爆轰反应及其与空气的相互作用,具体的讲,必须同时考虑炸药、爆轰产物、空气3 种组分,以及前两种组分间的反应动力学模型。对这种典型的多介质流动,有若干种算法可以选择。拉格朗日型方法可以得到无耗散的介质界面,但对大变形问题,需要进行网格重分。欧拉型方法中,也有一些解决方法,如采用较为成熟的Level Set 方法捕捉界面,但同样难以处理界面拓扑的大幅变化,而且界面处物理量不守恒,对于物理量变化剧烈的爆炸流场而言,这一问题可能是十分严重的;采用改进的虚拟流体方法[5](MGFM)可很大程度上改善这一问题,但仍未根本解决。近年来有学者陆续提出了一种新的多流体计算模型[6-7],对每种相(气、液、固)采用独立的连续、动量、能量方程来描述,同时求解一个附加的体积分数的方程,这一方法也在含能材料的爆轰模拟中得到了应用[8],其主要存在的问题是求解方程多,计算量大,而且方程是非守恒的。
在某型爆炸激波管的设计中,采用TNT 装药的爆炸来驱动产生空气中冲击波,圆柱形的TNT 药柱置于驱动管内,药柱与驱动管内壁间为静止空气。在驱动管出口处引爆药柱后,爆轰波沿药柱向管底传播,爆轰产物同时向侧面的空气中飞散,在管壁和管底上也引起很大的压力载荷。这一问题中流场的发展与爆轰波的传播过程密切相关,爆轰产物与空气间存在复杂的相互作用,二者间界面也经历了很大的变化。经过调研,目前的各种算法解决这一问题均存在一定程度的不足或缺陷,为此本文提出一种炸药、爆轰产物与空气3 种介质的混合模型,通过求解固定网格下的多组分Euler 方程组来解决这一问题。此混合模型在固相与气相间采用等压假设,满足体积可加性;在气相之间采用等温假设。炸药与爆轰产物均采用JWL 状态方程,反应模型为文献[9]提出的“点火—生长”模型,采用时空两阶精度的有限体积方法离散,采用AUSM+-up 格式计算通量。计算了空气中球形TNT 装药的爆炸问题,并将爆炸近区的超压、冲量等与实验结果进行了比较,验证了计算方法的有效性和精度,为爆炸激波管的模拟奠定了基础。
1 计算方法
1.1 控制方程
考虑化学反应的三维非定常Euler 方程组为


式中:ρ 为混合气体的密度;u、v、w 分别为x,y,z 方向速度;p 为混合气体压力;E 为气体的总能,E =,e 为混合气体的比内能,ρi为第i 种组分的密度;Qc为化学反应的放热项;σi为第i 种组分的生成率。在本文中,下标1 代表未反应炸药,下标2 代表产物气体,下标3 代表空气,于是有

1.2 状态方程
空气采用量热完全气体模型,状态方程为

式中:T 为气体温度;R 为气体常数;γ 为比热比。
炸药及爆炸产物均采用JWL 状态方程描述,其形式为

或


表1 炸药的状态方程参数Tab.1 Coefficients of JWL state equations
1.3 反应模型
反应模型采用Lee 等提出的“点火—生长”反应模型[9],具体形式为

式中:ρ0为炸药的初始密度;λ 为反应度,含义为爆炸产物的质量分数;I、G、x、y、z、γ 是与炸药有关的6个可调系数,Lee 等选择x=2/9,y =2/3,γ =4,其余3 个系数用拟合实验数据得到。Lee-Tarver 反应率模型描述了热点的形成和生长,(7)式中的第1 项表示热点的形成,第2 项表述反应的增长。其中(ρ/ρ0-1)是未反应炸药在冲击波作用下的相对压缩度。压缩度越大,冲击波所产生的热点就越多,温度也越高,反应也就越强。本文采用的模型系数如表2所示。

表2 “点火—生长”模型中的系数Tab.2 Coefficients for ignition and growth model
引入反应速率模型后,(2)式中源项的各分量就可写为:

式中Q0为单位质量炸药爆轰释放的能量。
1.4 离散方法
本文采用格心格式的有限体积方法离散控制方程(1)式,将无粘通量与反应源项同步求解,也即由n 时刻的流动变量Qn,根据(2)式分别计算无粘通量与反应源项,然后代入(1)式,更新流动变量为Qn+1.采用Green 公式计算单元内变量梯度,获得空间二阶精度;为了抑制振荡,采用了Venkatakrishnan 限制器;采用AUSM+-up[10]格式计算单元边界上的通量。时间推进采用二阶精度的4 步Runge-Kutta 方法。
AUSM+-up 是根据界面马赫数对通量进行分裂的,因此用来计算不同状态方程的流体时,只需要计算界面声速即可,无需考虑通量的Jacobi 矩阵,很适合计算状态方程形式复杂的问题。
2 混合物状态方程
为了推导混合物的状态方程,首先给出Mie-Grüneisen 状态方程对应的声速公式。对于满足Mie-Grüneisen 状态方程的流体模型,其压力可以由密度和内能显式地给出,状态方程的一般形式为p=p(ρ,e).比较常见的Mie-Grüneisen 状态方程包括理想和刚性气体状态方程、Van der Waals 状态方程、JWL 状态方程、Cochran-Chan 状态方程和BKW、HOM 状态方程等。
由熵的定义及热力学第一定律可以推导得出,对于状态方程为p =p(ρ,e)的物质,其声速可表示为
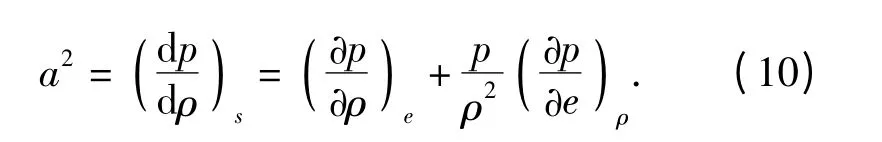
这样,就建立了声速与状态方程之间的关系,若已知物质的状态方程,就可根据(10)式求得其声速。
2.1 炸药与产物的混合物状态方程
文献[9]指出,使用JWL 状态方程计算爆轰问题时,在炸药与爆轰产物间应当采用等压假设,即同一个单元内的炸药和爆轰产物具有相同的压力,而温度可能不同[11]。根据这两个假设即可得到炸药与产物的混合物状态方程,过程较为简单[11],这里仅给出最后结果:

2.2 产物与空气的混合物的状态方程
爆轰产物与空气同为气态,在构造两者混合模型时,借鉴了气态爆轰计算中的模型,认为满足局部动量平衡和热力学平衡假设,也即在爆炸流场的任意一个流体微元内,这两种组分的温度、速度相同,压力满足分压定理。
观察JWL 状态方程(5)式或(6)式还可发现,如果令A=B=0,则JWL 状态方程就退化为量热完全气体的状态方程,JWL 状态方程中的ω 相当于完全气体中的(γ-1),γ 为比热比。因此,可以将完全气体状态方程写为JWL 状态方程的形式,下文均采用这一方法以简化公式的推导和书写。
采用上面的混合模型后,爆轰产物与空气的混合气体的状态方程可写为

2.3 炸药、产物与空气的混合物状态方程
当流体微元中同时含有炸药、爆轰产物与空气3 种组分时,炸药为固相,而产物与空气为气相,它们在微元内的分布情况可如图1所示。为了建立3组分的混合模型,将上述两种两组分混合模型结合起来,假设两种气体组分(爆轰产物与空气间满足动力学、热力学平衡和分压定理,而气体组分与固体组分(炸药)间具有体积可加性且压力平衡。具体地说,有如下4 点:1)每个流体微元的体积可分为两部分,分别为固体组分和气体组分所占据;2)气体组分间热力学平衡:T23=T2=T3,压力满足分压定理:p23=p2+p3;3)气体与固体组分间压力平衡:p1=p23,温度不等:T1≠T23;4)所有组分的速度都相等。

图1 炸药、产物与空气间的流体混合模型Fig.1 Fluid-mixture model of explosives,detonation products and air
微元内混合物的分布如图1所示。这种模型在物理上较为直观,并且在ρ1=0 时退化为爆轰产物与空气的混合模型,ρ3=0 时退化为炸药与爆轰产物的混合模型。下面推导此混合模型的状态方程:
首先考虑气相。在微元dV23内,爆轰产物和空气的质量分别为ρ2dV 和ρ3dV,在此微元内其密度分别为
根据(12)式可得微元dV23内压力与内能的关系式:
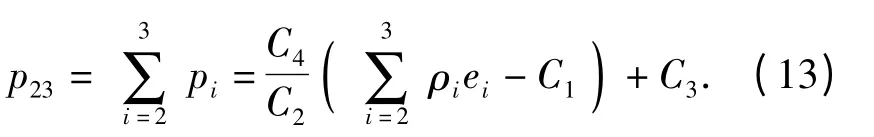
然后考虑固相,在微元dV1内,炸药的密度ρ'1=根据状态方程(5)式,有

联立(13)式与(14)式,根据压力平衡条件p =p1=p23,可得到包含炸药、爆轰产物、空气的混合物的状态方程:

式中:
可以证明,当ρ1=0 时,(15)式便退化为(12)式,即仅含爆轰产物与空气的混合物状态方程;当ρ3=0时,(15)式便退化为(11)式,即炸药与爆轰产物的混合物的状态方程。将(15)式分别对ρ 和e 求导,得到再根据(10)式便可得到此时的声速。推导过程比较繁琐,这里仅给出最后结果:

式中:

由上述推导可知,该流体混合模型可以处理包含炸药、爆轰产物、空气的流动问题,并且混合物的状态方程(15)式及声速公式(16)式均是显函数形式,无需迭代求解,计算效率很高。该方法同时具有流体混合型方法的固有优点,如:适合计算界面的大变形问题,无需进行任何特殊处理,给计算带来了极大的便利,但在流体界面处也不可避免地引入了数值耗散,导致捕捉到的流体界面是一个连续过渡的区域,界面附近的若干个单元内将产生人为的流体混合。此外,本文方法使用JWL 状态方程描述炸药和爆轰产物,使用完全气体模型描述空气,如何拓展至其他形式的状态方程仍有待研究。
3 空气中球形装药的爆炸
如引言所述,模拟爆炸波在炸药内的传播过程时,仅需考虑炸药与爆轰产物两种物质,模拟爆炸波在远场的传播过程时,可忽略炸药的影响,仅模拟爆轰产物与空气,甚至可以将爆轰产物简化为空气处理,目前对空中爆炸问题的数值模拟也绝大多数集中于这两种情况[3-4],但对于爆炸近区的流场,要同时考虑炸药、爆轰产物和空气3 种物质,相关的数值研究很少。事实上,这类问题可供对比的实验数据也极为有限,尤其是非球形装药的爆炸问题。为了校验本文数值方法,本节计算了球形装药的爆炸问题,并与实验结果进行比较。
当不考虑空气组分时,如凝聚态炸药中的爆轰波传播问题,(15)式自动退化为(11)式,此时计算程序的精度和有效性已得到了验证。但对于同时包含炸药、爆轰产物、空气3 种组分的问题,可供验证的实验数据尤其是非球形爆炸的近区实验数据几乎没有,为了校验本文方法,模拟了空气中球形装药的爆炸问题,重点考察爆炸近区的计算结果与实验值的比较。
采用一维球对称程序模拟了空气中球形装药的爆炸问题。装药为TNT,装药半径为0.1 m,装药量约为6.8 kg,在球心处点火。计算采用的反应模型为“点火—生长”模型,状态方程及反应模型中的系数来自文献[12].如图2所示给出了不同时刻的压力波形,可看出,15 μs 时,爆轰波仍在炸药中传播,未到达炸药与空气界面,爆轰波的峰值压力为46 GPa,爆速为6 810 m/s,略低于理论爆速6 849 m/s.C-J 点压力为18.86 GPa,也略低于理论值19.1 GPa.24 μs 时,冲击波已传至空气中,由于波后无反应区提供能量,冲击波波后压力迅速下降,远低于爆轰波波后压力。从图上可以看出,随着传播距离的增大,冲击波的波后压力逐渐下降,波速也在变慢。

图2 不同时刻的爆轰波压力波形Fig.2 Distributions of pressure at different times
如图3所示给出了42 μs 时冲击波附近的压力和密度曲线,在此图上可更清楚地看到爆轰波到达空气界面后的波系发展情况。爆轰波到达产物与空气的界面后,透射波为冲击波,在空气中传播;反射波为反射膨胀波,向爆心传播。爆轰波后的强稀疏波到达产物与空气的界面后,透射波为透射稀疏波,反射波为反射激波。透射稀疏波不停地追上空气中冲击波,使得波后峰值压力不断被削弱,冲击波波速下降。同样的,向爆心运动的反射激波不停追上反射膨胀波,在激波后产生反向运动的稀疏波。由此可见,计算得到的各种波系及流体界面结构清晰,反映了计算方法具有较高的精度和分辨率。
计算过程中沿径向每隔0.05 m 设置一个压力监测点,如图4所示给出了标尺距离为1.0、1.5、2.0 的3 个测点的超压时程曲线。标尺距离的定义为Rs=r/W1/3,r 为测点到爆心的距离(m),W 为装药量(kg)。

图3 42 μs 时的压力和密度曲线Fig.3 Distribution curves of pressure and density at 42 microseconds
关于空中爆炸的超压峰值随距离的变化,有相当多的实验数据与经验公式可供比较,但适用于爆炸近区的数据较少。本文主要采用了文献[13-16]中的一些数据,这些数据在离爆心较远的距离上能给出彼此接近的结果,但在装药近区有所差异。其中Baker 的数据是对许多理论和实验结果的汇编,具有很宽的适用范围;Henrych[14]和Brode[16]的经验公式在爆炸近区会给出偏大的结果;Henrych的经验公式在直至装药表面的范围内都是足够准确的。如图5所示给出了计算得到的超压峰值与实验结果的比较,可看出,计算结果与各实验值均符合很好,即使标尺距离小于时,计算结果仍然与Baker、Henrych、Kinney 等[15]的结果高度吻合,曲线中标尺距离最小的点距装药表面仅5 cm.

图4 标尺距离1.0、1.5、2.0 的3 个监测点的超压时间曲线Fig.4 Over-pressure waveforms at scaled distances of 1.0,1.5,2.0

图5 超压峰值与实验结果、经验公式的比较Fig.5 Comparison of peak over-pressure between computation and experiment and formula
取爆轰波到达装药表面的时刻为零时刻,如图6所示给出了冲击波到达的时间随标尺距离的变化情况,与Baker 的结果符合很好。如图7所示给出了超压冲量随标尺距离的变化情况,作为对比的分别是Baker 的汇编数据,Sadofskyi 的理论公式以及Henrych 的实验结果。在这里,不同文献的结果出现了数倍的差异,而本文计算结果落在了文献结果之间,与Baker 的结果更为接近,且变化趋势与Baker 的结果相同。
总的来说,计算结果与各种实验结果符合较好,反映了本文计算方法具有相当的准确性。

图6 冲击波到达时间的比较Fig.6 Comparison of arriving time

图7 超压冲量的比较Fig.7 Comparison of impulse
4 结论
提出了一种用于模拟爆炸近区中炸药、爆轰产物、空气等相互作用流场的数值方法。算法为固定网格下的欧拉型方法,引入了一种炸药、爆轰产物、空气3 种组分的混合模型,该模型中炸药及爆轰产物采用JWL 状态方程,空气采用理想气体模型,在固相(炸药)与气相(爆轰产物、空气)间采用等压假设,且体积可加;气相间满足等温假设及分压定理。该模型无需迭代求解,计算效率较高。计算了空气中球形TNT 装药的爆轰问题,得到了清晰的波系结构及流体界面,界面附近无非物理振荡,计算结果与现有实验值符合良好,验证了本文方法的有效性和计算精度,为下一步的应用打下了基础。
References)
[1] Zhou X Q,Hao H.Prediction of airblast loads on structures behind a protective barrier[J].International Journal of Impact Engineering,2008,35(5):363-375.
[2] Wu C,Hao H.Numerical simulation of structural response and damage to simultaneous ground shock and airblast loads[J].International Journal of Impact Engineering,2007,34(3):556-572.
[3] 宁建国,王仲琦,赵衡阳,等.爆炸冲击波绕流的数值模拟研究[J].北京理工大学学报,1999,19(5):543-547.NING Jian-guo,WANG Zhong-qi,ZHAO Heng-yang,et al.Study on the flow of the explosive shock wave around the wall numerical simulation[J].Transactions of Beijing Institute of Technology,1999,19(5):543-547.(in Chinese)
[4] 刘君,刘瑞朝,贾忠湖,等.爆炸波与物体干扰流场的数值模拟[J].空气动力学学报,2000,18(1):55-60.LIU Jun,LIU Rui-chao,JIA Zhong-hu,et al.Numerical simulation of blast interaction with bulidings[J].Acta Aerodynamica Sinica,2000,18(1):55-60.(in Chinese)
[5] Liu T G,Khoo B C,Yeo K S.Ghost fluid method for strong shock impacting on material interface[J].Journal of Computational Physics,2003,190(2):651-681.
[6] Saurel R,Abgrall R.A multiphase godunov method for compressible multifluid and multiphase flows[J].Journal of Computational Physics,1999,150(2):425-467.
[7] Abgrall R,Saurel R.Discrete equations for physical and numerical compressible multiphase mixtures[J].Journal of Computational Physics,2003,186(2):361-396.
[8] Chinnayya A,Daniel E,Saurel R.Modelling detonation waves in heterogeneous energetic materials[J].Journal of Computational Physics,2004,196(2):490-538.
[9] Lee E L,Tarver C M.Phenomenological model of shock initiation in heterogeneous explosives[J].Physics of Fluids,1980,23(12):2362-2372.
[10] Liou M-S.A sequel to AUSM,part II:AUSM+-up for all speeds[J].Journal of Computational Physics,2006,214(1):137-170.
[11] Clutter J K,Belk D.Simulation of detonation wave interaction using an ignition and growth model[J].Shock Waves,2002,12(3):251-263.
[12] Kury J W,Breithaupt R D,Tarver C M.Detonation waves in trinitrotoluene[J].Shock Waves,1999,9(9):227-237.
[13] Baker W E.Explosions in air:part 1[M].Austin:University of Texas Press,1974.
[14] Henrych J.The dynamics of explosion and its use[M].Amsterdam:Elsevier Scientific Publishing Company,1979.
[15] Kinney G F,Graham K J.Explosive shocks in air[M].New York:Spring-Verlag,1985.
[16] Brode H L.Numerical solution of spherical blast waves[J].Journal of Applied Physics,1955,26(6):766-775.
