含铝炸药作功能力和JWL状态方程尺寸效应研究

计冬奎，高修柱，肖川，武勇忠，杨凯

(1.西安近代化学研究所，陕西 西安，710065;2.中国兵器工业系统总体部，北京100089)

0 引言

含铝炸药在爆轰时可以产生高爆热，从而有较高的作功能力，是构成军用混合炸药的一个重要系列［1］。在设计含铝炸药战斗部时，需要这种炸药的作功能力和爆轰性能参数。这种炸药爆轰时在C－J面之前铝粉并不参加化学反应，在到达C－J 面时也远远没有反应完全;铝粉的反应是在C－J 面之后，当爆轰产物膨胀时才开始并逐渐完成的。因此，含铝炸药作功能力和爆轰产物状态方程参数在尺寸方面是否具有普适性是含铝炸药战斗部设计者需要考虑的重要因素。研究含铝炸药作功能力和爆轰产物状态方程参数的尺寸效应具有重要的理论和应用价值。

炸药爆轰产物状态方程是描述炸药爆轰C－J 状态之后的爆轰产物系统各物理量(压力、比容、温度和内能等)之间的关系式。这方面的研究对爆炸力学的研究和应用具有重要的意义。目前，已有多种发展比较成熟的爆轰产物状态方程形式。其中，JWL 状态方程是一种能比较精确地描述爆轰产物的膨胀驱动过程［2］，而且可以由试验方法确定的半经验状态方程。其形式为

等熵条件下，其形式为

式中:p 为爆轰产物的压力;V 为爆轰产物的相对比容;E 为爆轰释放的总能量。状态方程(1)式有6 个待定参数，其等熵形式(2)式的6 个待定参数为A、B、C、R1、R2和ω.

1 圆筒试验与结果

1.1 圆筒试验

圆筒试验确定了炸药爆轰产物侧向膨胀作功的标准试验方法［3］，这种方法可以定量地比较各种炸药的作功能力，并可将试验数据处理成JWL 状态方程，用于理论计算。试验采用高纯度(99.99%铜含量)的铜管，内装炸药，使其产生一维平面爆轰波，利用同步氩气弹发光作光源，对准圆筒某一截面，利用条纹扫描相机记录该截面表面位移与时间的关系，经过数据处理可获得该截面的时间—速度—位移曲线，求出铜管在爆轰产物驱动下的膨胀速度历程，衡量炸药侧向膨胀作功能力。

本次圆筒试验分φ25 mm 和φ50 mm 两种尺寸，待测的含铝炸药为以RDX 为主要成分的含铝炸药，采用压装成型工艺，试验样品尺寸分别为φ25 mm×300 mm 和φ50 mm×495 mm;圆筒材料为TU1 无氧铜，外径分别为φ30 mm 和φ60 mm;狭缝位置分别为距圆筒起爆端200 mm 和295 mm.试验装置如图1所示。

试验过程中，用固定于圆筒起爆端和末端的电探针测定炸药的爆速D，用GSJ 高速转镜相机拍摄圆筒在爆轰产物膨胀作用下狭缝位置处端面的膨胀过程。

1.2 试验结果

对含铝炸药φ25 mm 和φ50 mm 两种尺寸的圆筒试验各进行了3 发。狭缝位置处的圆筒在爆轰产物驱动下的膨胀过程光测的结果如图2所示。

从一端起爆装填在圆筒内的炸药试样，炸药爆轰后圆筒壁在爆轰产物作用下沿圆筒的径向和轴向作二维运动，膨胀距离(R－R0)与膨胀时间t 满足

图1 圆筒试验装置示意图Fig.1 Schematic diagram of the cylinder test

图2 含铝炸药圆筒膨胀过程光测结果照片Fig.2 Photograph of the cylinder expansion process for aluminized explosive

式中a、b、c、d 均为拟合系数。

圆筒的径向膨胀速度u 和圆筒的比动能E 分别为:

按最小二乘法原理对光测结果进行曲线拟合，可获得系数a、b、c、d 的值。

2 JWL 状态方程参数确定

2.1 基本方法概述

首先用解析分析方法求解出JWL 状态方程参数［4］;然后以这些参数为预估参数，用LS－DYNA 数值模拟计算含铝炸药两种尺寸圆筒的膨胀过程［5］，通过迭代优选方法，求出该炸药爆轰产物JWL 状态方程的参数值。

2.2 解析求解方法

由热力学关系式

(2)式和(6)式，可得JWL 状态方程的等熵内能形式:

式中Es为爆轰产物的等熵内能。

设Es，V=1爆轰产物气体膨胀释放的有效总能。对爆轰产物膨胀驱动过程，将满足守恒关系

式中:Egk(V)为爆轰产物的动能;EM(V)为被驱动金属的动能。设

EGurney(V)为系统的Gurney 能量，则由(8)式和(9)式得

可以看到，Es，V=1就是爆热Q，可由

计算得到，式中:pC－J为C－J 爆压;γ 为多方指数。

EGurney(V)可由改进的Gurney 公式得到:

式中:mM/mE为被驱动金属与炸药的单位长度质量比;u 为被驱动金属的速度，对圆筒实验，即为圆筒膨胀速度，可由(4)式求得;n 为装药几何参数，对圆筒实验，n=2，则(12)式变为

为将能量守恒关系式同圆筒实验测试得到的圆筒膨胀过程联系起来，需知相对比容V 随膨胀距离(R－R0)的变化关系。通过二维流体动力学数值模拟计算，拟合得到一般炸药的φ25 mm 圆筒试验的关系为:

这样，由上述关系式和圆筒试验测试结果的联立方程组，就可解析求解出JWL 状态方程的6 个参数估算值。

JWL 状态方程(7)式的右边3 项，可分别视为高压、中压和低压3 个阶段的贡献项:

在低压阶段(V ＞6)，可取

通过对V ＞6 阶段的试验参数的进行计算，可求解得到C 和ω.

在中压阶段(2 ＜V ＜5)，可取

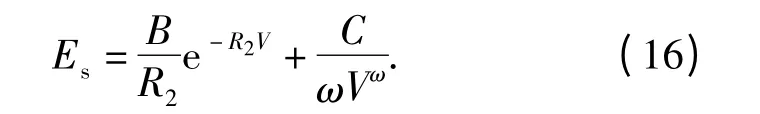
由(15)式求解得到的C 和ω，通过对该中压阶段的试验参数进行计算，可求解得到B 和R2.

A 和R1可由C－J 参数确定。在C－J 点，有:

由实测爆压pC－J、爆速D、多方指数γ，和已经计算得到的B、R2、C 和ω，即可求得A 和R1.

2.3 数值模拟与结果

在LS－DYNA 程序计算圆筒爆炸的二维轴对称问题中，建立Lagrange 坐标(R，Z，t)，即质量的原始坐标为(R，Z)计算中跟踪质量，按照试验中标用的尺寸。

在计算中，不计爆轰波的结构仍采用瞬时爆轰模型，即LS－DYNA 中的“MAT－HIGH EXPLOSIVEBURN”模型，不计炸药的强度效应，只要给出密度，爆速与爆压就可以了，另外，在Lagrange 计算中，适用“EOS－JWL”模型，除了需要给出JWL 方程中的A、B、C、R1、R2和ω 预估值外，还需给出初始能量即爆热E0和初始相对体积。

分析偏离趋势，适当地修正预估参数，在代入程序中进行计算，计算逐渐接近试验测试结果。经多次修正和计算，含铝炸药φ25 mm 圆筒试验模型的膨胀过程R(t)计算结果与试验结果基本相符。再将含铝炸药φ25 mm 圆筒试验计算得到的参数作为预估参数代入含铝炸药φ50 mm 圆筒试验模型进行数值模拟计算，并对参数作微量调整，直至计算结果与试验测试结果基本一致。

含铝炸药2 种装药直径圆筒试验圆筒膨胀过程数值模拟计算结果与试验结果比较，如图3～图4所示。可看出，试验测试结果与数值模拟结算结果的相对误差基本控制在1%左右，符合JWL 状态方程参数确定的要求。

3 JWL 状态方程参数

图3 含铝炸药φ25 mm 圆筒的径向膨胀速度与膨胀距离的关系Fig.3 Relation between radial expansion velocity and distance of φ25 mm cylinder of aluminized explosive

图4 含铝炸药φ50 mm 圆筒的径向膨胀速度与膨胀距离的关系Fig.4 Relation between radial expansion velocity and distance of φ50 mm cylinder of aluminized explosive

通过对含铝炸药两种装药直径圆筒试验的数值模拟计算和综合分析，确定得到了含铝炸药爆轰产物的JWL 状态方程参数，如表1所示。含铝炸药密度为1.868 g/cm3.

表1 含铝炸药JWL 状态方程参数Tab.1 Parameters of the JWL equation of state for aluminized explosive

由图3、图4和表1比较可见:1)从含铝炸药φ25 mm 和φ50 mm的曲线看出，φ50 mm圆筒膨胀至60 mm 处的速度高于φ25 mm 圆筒膨胀至30 mm处的速度，说明大尺寸的含铝炸药作功能力较强;2)φ50 mm 圆筒JWL 状态方程参数与φ25 mm 圆筒JWL 状态方程参数有一定的差异，这表明，大尺寸的含铝炸药相比小尺寸同种炸药，A 稍增大，B 增大较多，C 基本不变，R1稍小，R2增大较多，ω 稍小。这是由于当铝粉颗粒度较大时，把这些大颗粒的铝粉从吸热熔化到气化需要较长的时间，氧化反应一般不易短时完成，从而加大了反应区宽度，同时又有一部分铝粉与其他爆轰产物进行热交换，进一步发生二次化学反应，加大了产物的作功本领。

建议在工程应用中，计算小尺寸含铝炸药爆炸性能时，采用φ25 mm 圆筒试验对应的JWL 状态方程参数;计算大尺寸含铝炸药爆炸性能时，则采用φ50 mm 圆筒试验对应的JWL 状态方程参数。

4 结论

通过φ25 mm 和φ50 mm 两种药柱尺寸下圆筒实验结果推导其作功能力和获得JWL 与尺寸效应的关系，得到如下结论:

1)大尺寸的含铝炸药药柱作功能力较强。

2)大尺寸的含铝炸药药柱相比小尺寸同种炸药药柱，A 稍增大，B 增大较多，C 基本不变，R1稍小，R2增大较多，ω 稍小。

References)

［1］ 孙业斌，惠君明，曹欣茂，等.军用混合炸药［M］.北京:兵器工业出版社，1995.SUN Ye－bin，HUI Jun－ming，CAO Xin－mao，et al.Military composition explosives［M］.Beijing:The Publishing House of Ordnance Industry，1995.(in Chinese)

［2］ Lee E L，Hornig H C，Kury J W.Adiabatic expansion of high explosive detonation products，UCRL－50422［R］.San Francisco:University of California，1968.

［3］ Kury J W，Hornig H C，Lee E L，et al.Metal acceleration by chemical explosive［C］∥4th Symposium on Detonation.White Oak:Office of Naval Research，1965:3－13.

［4］ Smirnov A S，Shkalyabin I O，Kolganov E V.Determination of JWL equation of state parameters using the Gurney equation appraximation［C］∥9th Symposium on Detonation.Portland:Office of Naval Research，1989:498－505.

［5］ 时党勇，李裕春，张胜民，等.基于ANSYS/LS－DYNA 8.1 进行显式动力分析［M］.北京:清华大学出版社，2005.SHI Dang－yong，LI Yu－chun，ZHANG Sheng－min，et al.Obvious dynamical analysis based on ANSYS/LS－DYNA 8.1［M］.Beijing:Tsinghua University Press，2005.(in Chinese)