钛合金切削力建模与试验研究

高连生，袁云霞，张 辉

（北京航空航天大学 机械工程及自动化学院，北京 100191）

随着航空航天技术的发展，越来越多的钛合金结构件被采用。然而，钛合金是典型的难加工材料，其具有导热性系数低、高温化学活性高和弹性模量小等特点。随之而来的是低加工效率、低加工品质及刀具磨损严重等问题，这些已经成为航空航天制造领域突出的难题。

切削力是研究切削过程的重要物理量之一，其大小和变化对工件加工品质、刀具磨损和寿命等具有影响。发展钛合金高速切削技术，准确地预测切削力，对于优选切削用量、刀具结构参数以及提高加工精度，具有积极的指导意义。

1 钛合金的切削特性

钛合金切削产生的切屑为锯齿形切屑，一些学者对锯齿形切屑成形机理进行了研究，并解释为绝热剪切（或热塑性失稳）[1～3]，其实质为材料由于热特性差，切削时产生局部高温，使得材料的热软化效果，超过了加工硬化的效果，造成材料软化和屈服，剪切区强度下降，形成集中剪切滑移。

Komanduri[4,5]等人认为，钛合金切削中锯齿形切屑的成形，可以分为两阶段：在第一阶段，主剪切区产生塑性失稳和应变集中；在第二阶段，刀具运动使前刀面上的材料变成切屑。就每一节切屑而言，是先发生小的塑性变形，而后发生塑性失稳，与下一节切屑发生剪切滑移。

钛合金切削时的剪切滑移变形，集中在很窄的区域，剪应变和应变速率均很大，而切屑其他部分的变形相对很小，集中剪切滑移的宽度，只有数微米到数十微米，与普通切削相比，需要考虑切削过程中的尺度效应。

应变梯度理论，已成功解释了材料微观变形时的尺度效应，Liu应用泰勒位错的非局部应变梯度理论，定义材料的本构方程[6]，仿真铝A15083-Hll6的微切削过程时，考虑了应变梯度效应，比较了有无应变梯度效应仿真结果的差异，认为考虑材料的应变梯度，能更好的表示切削过程中的尺度效应。

本文基于应变梯度理论，建立了钛合金切削力预测模型，并设计了正交切削试验测量切削力，比较测量值与计算值，验证了切削力模型的可靠性。通过分析试验结果，阐明了切削参数对切削力的影响规律。

2 基于应变梯度理论的钛合金切削力预测模型

钛合金切削变形中的集中剪切滑移宽度，只有数微米到数十微米，可认为只有单一剪切面，但此剪切面相对刀具是运动的。为简化模型，只集中剪切滑移变形，其余部分变形可忽略不计，则根据力的平衡原理，模型中产生集中剪切滑移所需的作用力决定切削力。在塑性失稳开始瞬间，剪切面滑过刀尖点，产生集中剪切滑移，因此在塑性失稳瞬时，对切削过程起决定作用。

此时，模型类似Merchant切削模型，但随着切削的进行，剪切面以切屑速度向上移动。所以，以塑性时刻失稳为参考，切削力模型为

其中，

切向力Ft沿切削速度方向；

进给力Ff沿切削厚度方向；

aw为切削宽度；

ac为切削厚度；

β为摩擦角；

Ф为剪切角；

γ0为刀具前角；

τs为剪切应力。

Taylor位错理论描述了剪切应力与位错密度的关系，表示为

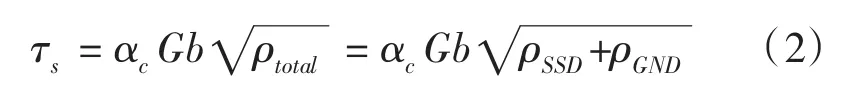
其中，

材料中常系数αc取0.3～0.5[7]；

G为剪切模量；

b为伯格斯矢量的大小；

ρtotal为总位错密度；

ρSSD为统计存储位错密度；

ρGND为几何必需位错密度。

统计存储位错，表示的材料单轴拉伸参考流动应力σref可从下式得出

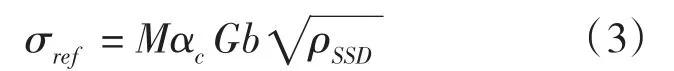
几何必需位错密度ρGND与有效应变梯度η之间的关系如式（4）

流动应力与剪切应力之间的关系可表示为

有效流动应力σ计算为

将式(3)和式(4)代入式(6)，得

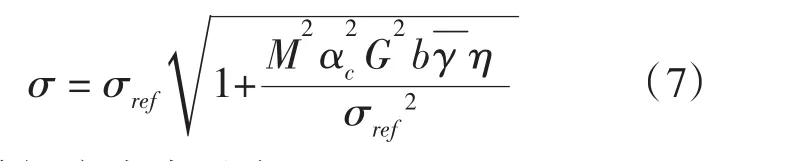
从而，剪切应力表示为

Joshi模型基于平行剪切区的有效应变梯度为[9]

其中，L为剪切区长度。

集中剪切滑移带为厚度△y很小，只有数微米到数十微米，可认为集中剪切滑移带是厚度为△y的平行剪切区，应变梯度可适用Joshi模型，此时的L等于梯形节段下边界长度

将式(9)和式(10)代入式（8），得

代入式(1)，得

3 正交切削试验

3.1 试验条件

切削力试验测量系统，一般由机床、刀具、工件、测力仪、电荷放大器、数据采集箱、数据采集系统及PC机组成，其组成原理如图1所示。

图1 测量切削力的试验系统组成原理图

工件：钛合金Ti-6Al-4V（TC4），尺寸为 150 mm×150 mm×150 mm，σb=1 100 MPa，σs=1 000 MPa，δ=14%。

刀具：三特维克R300 1240 E-PM GC1025型号刀片，刀杆直径为32 mm，两齿。

铣削方式：顺铣。

切削测力仪：Kistler 9257B测力仪，测量范围-5～5 kN，灵敏度7.5 pc/N。

机床：北航自行研制的试验平台，三坐标铣床。主轴功率4.5 kW，最高主轴转速8 000 r/min。

3.2 试验方案与分析

试验采用正交试验法，试验采用的因素有：切削速度 νc，每齿进给量 fz，切削深度 ap，切削宽度 ae。

各因素均取3个水平，进行四因素三水平的等水平正交实验L9(34)。

表1 切削力试验L9(34)正交试验设计表

表2 切削力试验结果

由图2和图3可知，Fy的试验值和模型计算值相差很小，基本一致；Fx的试验值与模型计算值，有的很接近，有的相差较大，但基本在合理范围内变动。

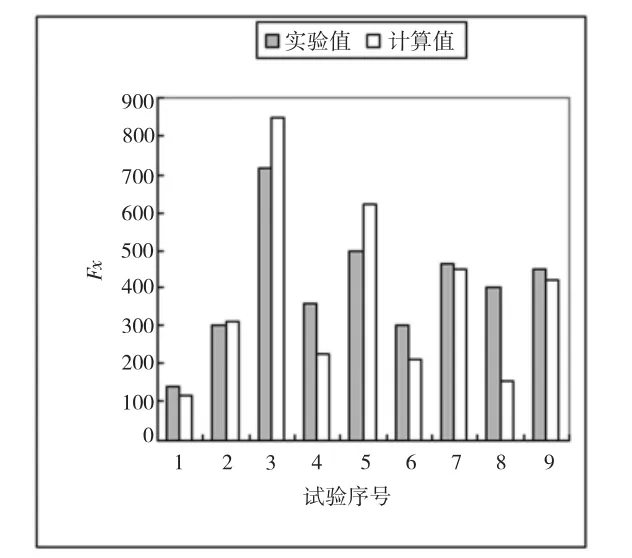
图2 Fx试验值与计算值两两比较

图3 Fy试验值与计算值两两比较

表2中，比较了X向分力和Y向分力的试验值与模型计算值，去除一个异常值，结果表明Fx误差不超过30%，平均误差低于20%，Fy的误差约为10%，平均误差低于10%。误差分析结果表明，模型具有一定合理性。

根据表3的试验结果，将各因素三水平所对应的切削力取平均值，记录于直观分析表并据此做出表中各因素对切削力影响的直观图。可以做出直观分析表3，由此得出切削力直观分析图4（a）、（b）、（c）、（d），从中可以看出各切削参数对切削力的影响程度及变化趋势。

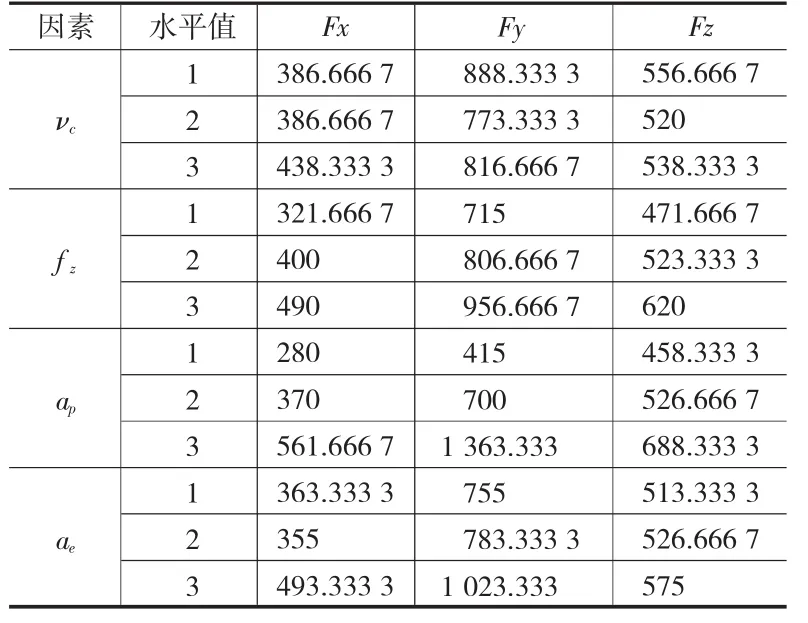
表3 正交设计实验结果的直观分析表

图4 切削参数对切削力影响的直观分析

切削力的大小和切削参数的选择，有着直接的关系，不同的切削参数，对切削力变化起着不同的作用。

由图4(a)可知，进给力和切深抗力变化极其微小，主切削力略有变化，但变化较小，说明高速切削钛合金时，切削速度对切削力的影响较小。

由图 4(b)、(c)、(d)可知，随着切削用量的增加，x、z向分力均略有增加，且近似呈线性增加，但总的说来，Fz随切削参数的变化不大。3个方向分力随参数变化的程度不同，对y向分力影响最大，体现在Fy近似直线，斜率的绝对值比另外两直线的要大；对3个方向切削力影响程度的大小顺序都为：切削深度ap＞每齿进给量fz＞切削宽度ae＞切削速度νc。

4 结束语

建立了基于应变梯度理论的钛合金切削力预测模型，切削力模型预测值与试验值相比，平均误差不超过5%，说明模型具有一定的合理性，切削中应用应变梯度理论预测切削力是合理的。

进行正交切削实验，对钛合金TC4以不同的切削用量进行切削，测量切削力，应用多因素直观分析法分析切削力试验值，可得：在钛合金高速切削中，主切削力基本大于进给力和切深抗力；主切削力随着进给速度、轴向切深、切削宽度的增大而会增大，减小而减小，这主要是因为这些参数变化，直接改变切削面积大小，而切削力随切削面积变化；切削用量对切削力影响程度大小顺序为：切削深度ap＞每齿进给量fz＞切削宽度ae＞切削速度νc。

[1]C Zener，J H Hollomon．Problems in Non—elastic Deformation of Metals[J]．Journal of Applied Physics，1946，17(2)：69-82.

[2]R Recht．Catastrophic Thermoplastic Shear[J]．Transactions of ASME，Journal of Applied Mechanics，1964，186(31)：189-193.

[3]M C Shaw，A Vays．The Mechanism of Chip Formation with Hardened Steels[J]．Annals of the CIRP，1998，47(1)：77-82.

[4]R Komanduri，R Brown．On the Mechanics of Chip Segmentationin Machining[J].Journal of Engineering for Industry,Trans，ASME，1981，（103）：33-51.

[5]Takehara M，Matrumoto Y，et al.Inlerlaminar Shear Strength of C/C Composites at Elevated Temperature[J].Tanso,1996,173(5):168-171.

[6]R Komanduri，B F Von Turkovich．New Observations on the Mechanism of Chip Formation when Machining Titanium Alloys[J]．Wear，1981，（69）：179-188.

[7]K W Kim，W Y Lee，H Sin.A Finite Element Analysis for the Characteristics of Temperature and Stress in Micro-machining Considering the Size Effect[J].International Journal of Machine Tools&Manufaeture，1999，（39）:1507-1524.

[7]M F Ashby.The Deformation of Plastically Non-homogeneous Alloys[J].Philosophical Magazine,1970，(21):399-424.

[8]A Arsenlis，D M Parks.Crystallographic Aspects of Eometrically-necessary and Statistically-stored Dislocation Density[J].Ac ta Material，1999，47(5):1597-1611.

[9]S S Joshi.An Explanation for the Size-effect in Machining Using Strain Gradient Plasticity[J].Journal of Manufacturing Science and Engineering,2004，(126):679-685.