多调制源信号的循环平稳分析及仿真
2012-02-20王小卉杨洁明
王小卉,杨洁明
(1.湛江师范学院 机电工程系,广东 湛江 524048;2.太原理工大学 机电研究所,山西 太原 030024)
在通信、遥测、雷达和旋转机械等系统中,经常会遇到很多随机信号,其非平稳特性表现为一定的周期性,这类信号统称为“循环平稳信号”。此类信号的统计特征参量虽然是时变的,但由于其自身独特的周期平稳性,使其单次采集到的记录,具有周期遍历特性,这种“循环平稳性能”,使得这类随机信号的分析处理得以实现。
传统统计信号处理方法在处理循环平稳信号时,都假定信号是平稳的,忽略了信号的循环平稳性,不能实现对循环平稳信号的最佳处理。因此,人们开始探索充分利用信号循环平稳特征的新的信号处理方法,广泛地应用于通信、语音处理、故障诊断等多种领域[1]。
由于机械故障信号一般都是复杂的多调制源调制调幅信号,本文就以多调制源信号为例,研究二阶循环平稳分析的解调性能,改进分析方法总结规律,为更好地分析实际故障信号奠定理论基础。
1 循环平稳信号特性[2]
通常情况下,随机信号统计特征,呈周期或多周期(各周期不能通约)变化。对循环平稳信号,假设某一信号为x(t),式(1)就是循环统计量的数学表达式。

其中,cx(t,τ)k是 x(t)的 k 阶时变统计量。
最常用的统计量为均值(一阶统计量)、相关函数与功率谱密度函数(二阶统计量)。一阶循环平稳信号,是指此信号的一阶循环统计量(信号的均值)是时间的周期函数的信号。
由一阶循环平稳推广,可得K阶循环平稳信号的定义:若随机过程x(t)从一阶到K阶的各阶时变统计量都存在,并且它们都是时间的周期函数(其中每阶的循环周期可能有多个,且各阶循环周期一般不同),则称该随机过程为K阶循环平稳信号。
因此,当K=1时,对应着一阶循环平稳信号;当K=2时,对应着二阶循环平稳信号。典型的二阶循环平稳信号,是正弦波信号被一个有限带宽的随机信号调制后所得的信号。
本文研究多调制源的调制调幅信号,也是一个二阶循环平稳信号,其数学模型为

其中,
A、B、C为幅值;
ft1指调制频率1;
ft2指调制频率2;
fz1指载波频率1;
fz2指载波频率2。
2 循环平稳分析相关概念
对二阶循环信号x(t)以T为周期进行采样,时变自相关函数为
R(t,τ)=E{x(t+τ/2)x*(t-τ/2)},
进行时间平均后写成傅里叶级数形式为

其中,
Rα(τ)就是循环自相关函数(Cyclic Autocorrelation Function,简称 CAF),表示为

信号x(t)循环自相关函数的Fourier变化,得到

Sα( f)就是信号的循环谱(也称为谱相关密度函数 Cyclic Spectrum Density,简称 CSD)。
4 信号仿真
本文采用的信号数学模型如式(2),设此仿真信号中
A=1;B=1;C=2;
调制频率 1,ft1=6 Hz;
调制频率 2,ft2=12 Hz;
载波频率 1,fz1=60 Hz;
载波频率 2,fz2=200 Hz。
从公式上来说,此信号可以看做是一个单纯调幅信号和一个单纯调频信号的叠加,即

调幅信号

调频信号

第一步:计算信号的循环自相关函数,做其三维谱图可勉强观察到ft1、2 ft1、fz1以及fz2,但是信息冗余,交叉干扰严重。循环频率α(Hz)。
第二步:作循环自相关τ=0处的单切片图如图1。
可在低频处看出两个频率:调幅信号的ft1,调频信号的调制频率ft2。

图1 循环自相关单切片分析τ=0
高频处有不易分辨有用频率信息:谱线在120 Hz左右最密。
这是由60 Hz的载波频率引起的,反映了调幅部分的载波及调制频率[60 Hz及其一倍边频(60±6)Hz]的信息。
如果忽略这一簇谱线,则可清楚地发现:在100~200 Hz范围内,谱线的排列和200~300 Hz范围内的谱线排列是一样的,并且关于200 Hz对称。而且在400 Hz处,有不受混频干扰的载波信号及其关于调频频率的多个边频。反映了调频部分的载波及调制频率[200 Hz及其多个边频(200 ±12)Hz、(200 ± 24)Hz、(200±36)Hz等]的信息。
第三步:做信号调制频率处的循环自相关与谱相关切片谱图,如图2所示。
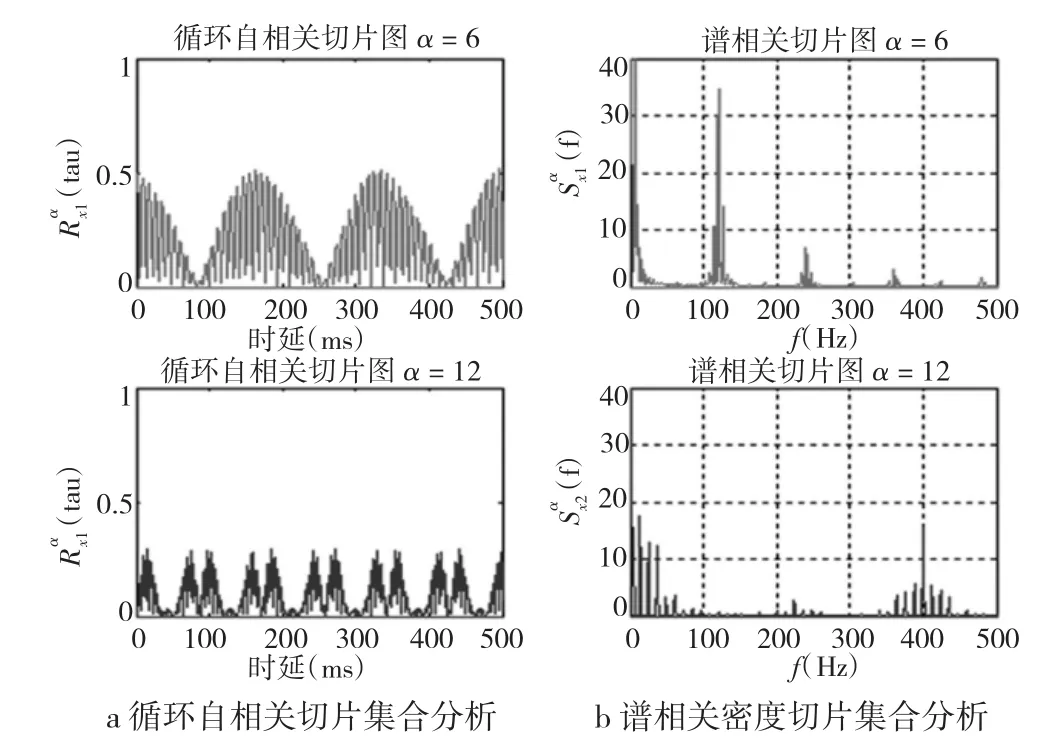
图2 特征频率处切片集合图
分析此图,总结如下:
(1)α=6 Hz的谱相关切片图,是相当于是对其循环自相关的FFT变换。在此循环自相关切片图中,可以看到信号在时延域中呈循环特性,而相应的谱相关图中则可清楚地发现ft1、2 ft1、2 fz1及其边频2 fz1±n ft1、4 fz1及其变频 4 fz1±n ft1、6 fz1及其边频 6 fz1±n ft1等有的能量峰值出现(n 取 1,2,3,…,取值越大,峰值越小)。
为了便于比较,又做调频信号

在特征频率α=6 Hz时的循环谱相关切片图,发现两者的的切片图表达的信息一致。即α取信号调制频率时,可以调解提取出该调幅信号的调制频率与载波频率。
(2)α=12 Hz的谱相关切片具有调频信号的特征。主要反映的是ft2及其倍频n ft2、2 fz2及其倍频2 fz2±n ft2(n取1,2,3,…,取值越大,幅值越小),与调频信号

在α=12 Hz的信息差不多,不同的是此图在f=240 Hz及其一倍边频处(240±6)Hz多出现了能量较低的一小组峰值,反映了调幅信号x1的调制与载波频率。
(3)从图中还可以清楚地发现,调幅信号与调频信号切片图的异同:在α取调制频率频率时,它们低频处出现的能量峰值的,都是是调制频率及其倍频;而高频处则都是载波及其边频,但调幅信号的这种切片图中,有载波频率的倍频,载波频率附近的边频也比较少(通常只有一倍边频),而调频信号中没有载波频率的倍频,且此载波频率附近会出现多组边频。
基于谱相关的这种调解特性,可以判别信号以及频率的类型。
3 结束语
本文阐明了循环平稳信号的特征及其适用信号处理方法。在此基础上,以较为复杂的调制调幅信号为仿真对象,分别分析了它的三维二阶循环自相关谱图,τ=0处的循环自相关单切片图,结果表明三维图运算量大,所得的信息冗余且频率之间干扰严重,取其切片图中也同样存在交叉干扰。
为更清楚地调解出复杂信号中的信息,本文提出了调制频率处的循环自相关与谱相关切片分析法。多调制源调幅信号、多频率成分相加信号的循环相关解调分析表明,循环相关解调分析可以排除交叉因素,有效分离出复杂信号中蕴涵的各调制源和载波源,为更好地分析实际故障信号奠定理论基础。
[1]黄知涛,周一宇,姜文利.循环平稳信号处理与应用[M].北京:科学出版社,2006.
[2]毕 果.基于循环平稳的滚动轴承及齿轮微弱故障特征提取应用研究[D].上海:上海交通大学,2007.
[3]丁 康,孔正国,李巍华.振动调频信号的循环平稳解调原理与实现方法[J].振动与冲击,2006,25(1):6-10.
[4]J Antonia,F Bonnardotb,A Raada,M El Badaouib.Cyclostationary Modelling of Rotating Machine Vibration Signals[J].Mechanical Systems and Signal Processing,2004,(18):1285 -1314.
[5]A V Dandawate and G B Giannakis.Nonparametric Polyspectral Estimations for Kth-Order(Almost)Cyclostationary Processes[J].IEEE Trans,on Information Theory,1994,40(1):67-84.
[6]李 敏,王小卉,杨洁明.基于循环谱密度切片集合分析法的轴承故障诊断[J].煤矿机械,2010,31(5):244-246.
