航空薄壁框类零件铣削加工表面质量研究

李初晔, 孙彩霞, 王增新

(北京航空制造工程研究所, 北京 100024)

0 引言

目前在航空航天制造业中，周铣是加工整体梁、框、肋类等大尺寸弱刚性薄壁结构件及发动机叶片最为典型的方法.由于工件的弱刚性特征，切削力作用下引起的工件和刀具变形，成为导致加工误差的主要因素，严重影响工件的加工精度和表面质量，为此国内外很多学者致力于工件表面加工误差的预测研究[1].铣削力的大小对加工精度和加工质量有着直接的影响，研制实用且预测精度较好的铣削加工过程计算机仿真模型并进行深入研究,实现动态铣削力和加工变形的程序预测，进而优化切削用量是铣削加工研究中值得关注的问题[2,3].

铣削加工过程中造成零件表面加工误差的原因有多种，总结起来主要有以下几个方面[4].

(1)加工中的热变形.铣削过程中随着铣削深度和进给量的增加，刀具与待加工件摩擦加剧，在刀具与待加工件内集聚了大量的切削热，材料受热膨胀，但由于受到装夹约束的限制，产生的热应力强迫待加工件改变形状，加工完成后去除约束变形回弹使加工面产生位置误差.

(2)材料切除过程中发生很大的塑性变形，当约束解除后，经过弹性恢复在零件内产生残余应力和残余变形，使零件产生加工误差.

(3)刀具和待加工件由于刚性不足，在铣削力作用下自身产生较大的变形，在切除材料过程中发生欠切和过切现象，造成加工误差.

(4)切削颤振.当铣削力的频率接近于刀具工件系统的固有频率时，会激发共振，振幅扩大，造成材料的实际切除量与理论值之间存在较大偏差，使加工表面产生误差[3].

目前，铣削加工向高速高效方向发展，主轴转速一般在每分钟万转以上，因此进给速度也得到极大地提高.每次加工可以分为粗铣和精铣两个阶段，在粗铣阶段保持较大的每齿进给量，从而使进给速度保持较高水平，以提高加工效率.这阶段由于每齿进给量大，铣削厚度大，因此产生较多热量，去除材料时的塑性变形也较大，加工误差主要由热变形和塑性残余变形产生.

在精铣阶段，特别是对薄壁深腔框类零件的加工，此时壁板已经很薄，铣刀细而长，刀具工件是一个弱刚性系统，在铣削力作用下发生较大变形，精铣阶段由于铣削厚度减小，塑性残余变形和产生的热量都较少，因此热变形和残余变形在这阶段是次要的.本文分析铣削力下的刀具工件系统的变形，由于铣削方式的不同造成材料的欠切和过切，从而使加工件产生的误差.

1 铣削力计算

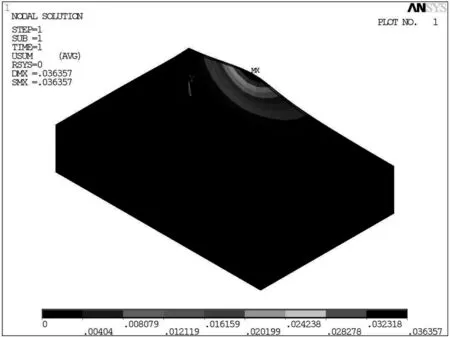
图1 有限元仿真得到的第一主应力分布

目前在研究领域铣削力的获得通常采用三种方法[5,6]，即多元回归分析、切削过程有限元数值仿真和微元切削力建模等.多元回归分析可得到相应的经验模型公式，不用考虑切削机理和材料去除过程，寻找出切削力和切削参数背后的数学规律.通常采用指数模型作为铣削力的最大值模型，对实验测定的多组数据进行数值拟合可求出系数值.该模型的优点是数学原理简单，但也存在明显的缺点.

切削过程有限元数值仿真能较真实地模拟加工过程的物理本质，通过仿真可得到加工表面位置偏差和残余应力分布规律，为优化加工参数提供理论依据.通过有限元仿真得到的第一主应力分布如图1所示.

微元切削力建模基于对切削机理分析，通过研究刀齿铣削过程，建立动态铣削加工计算模型，以直齿及螺旋齿立铣加工过程为研究对象，导出铣削力、铣削效率与切削用量的关系.铣削中刀齿经过切入和切出材料阶段，图2为顺铣加工示意图，图3为四齿螺旋铣刀顺铣一周的铣削力预测.铣削力计算程序分为输入参数模块、计算模块、数据输出模块等三部分，通过变换参数可以对不同铣削方案进行铣削力计算， 实际加工验证表明，该方法对铣削力预测精确度较好.

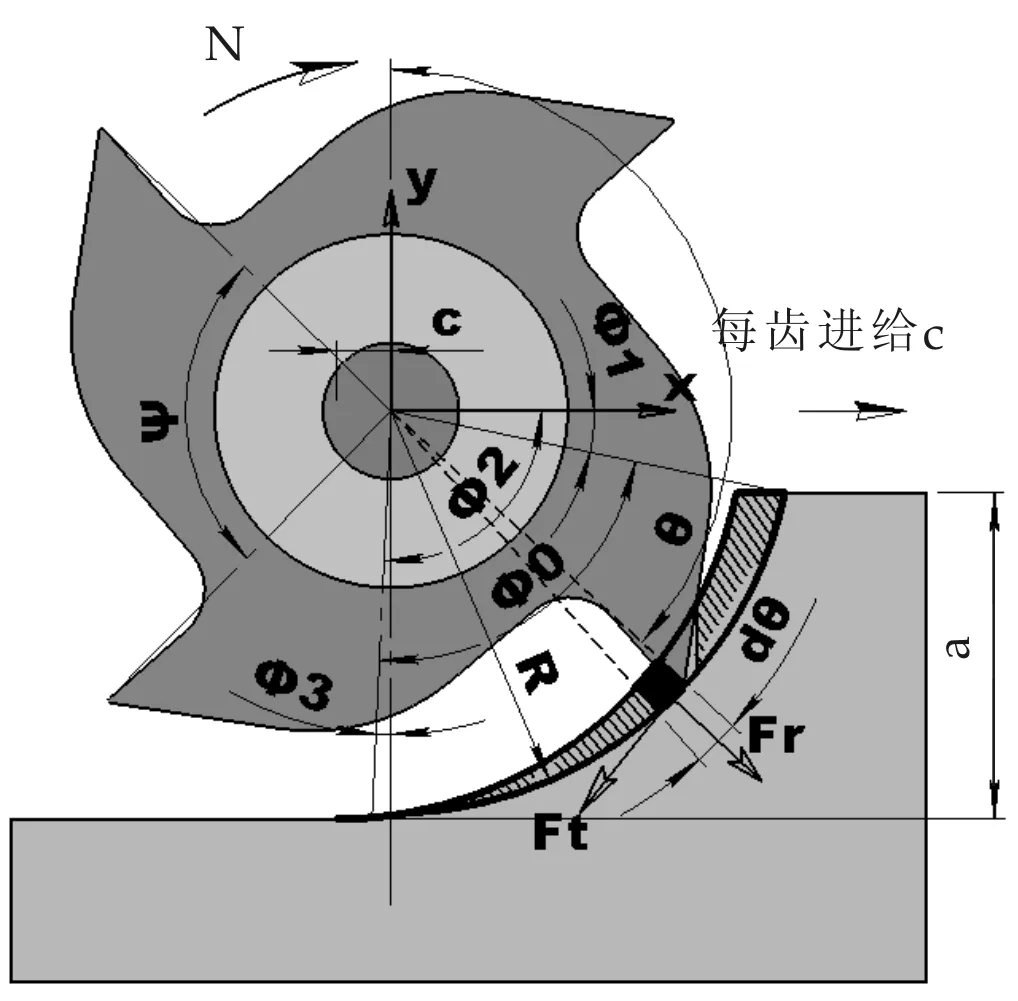
图2 顺铣微元切削模型

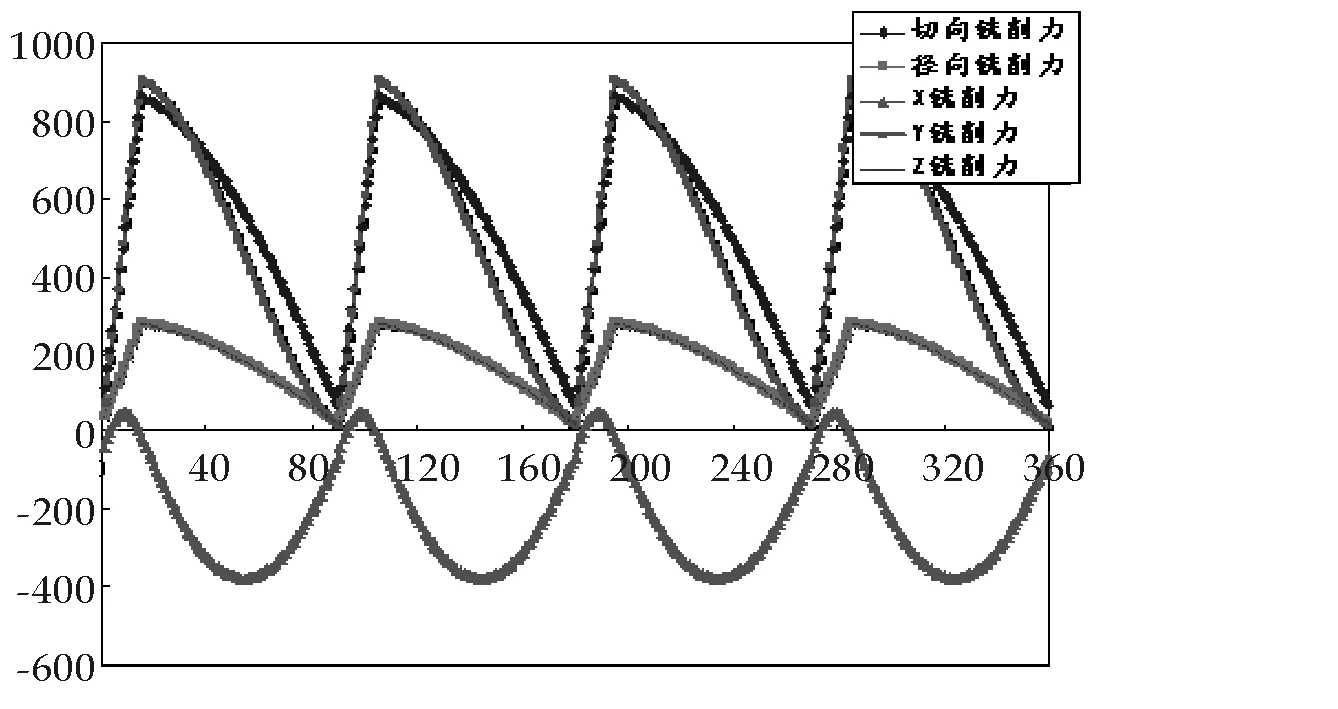
图3 四齿螺旋铣刀顺铣一周的铣削力预测

2 刀具弯曲对加工表面质量的影响

铣削时由于刀齿的切入切出，在加工表面会留下齿痕.当铣刀为直齿刀时，刀齿刃平行于刀轴线，若不计刀具的弯曲效应，齿刃在同时刻点或主轴转角时切出工件，在径向最浅切削厚度处形成齿痕，齿痕平行于刀轴线.

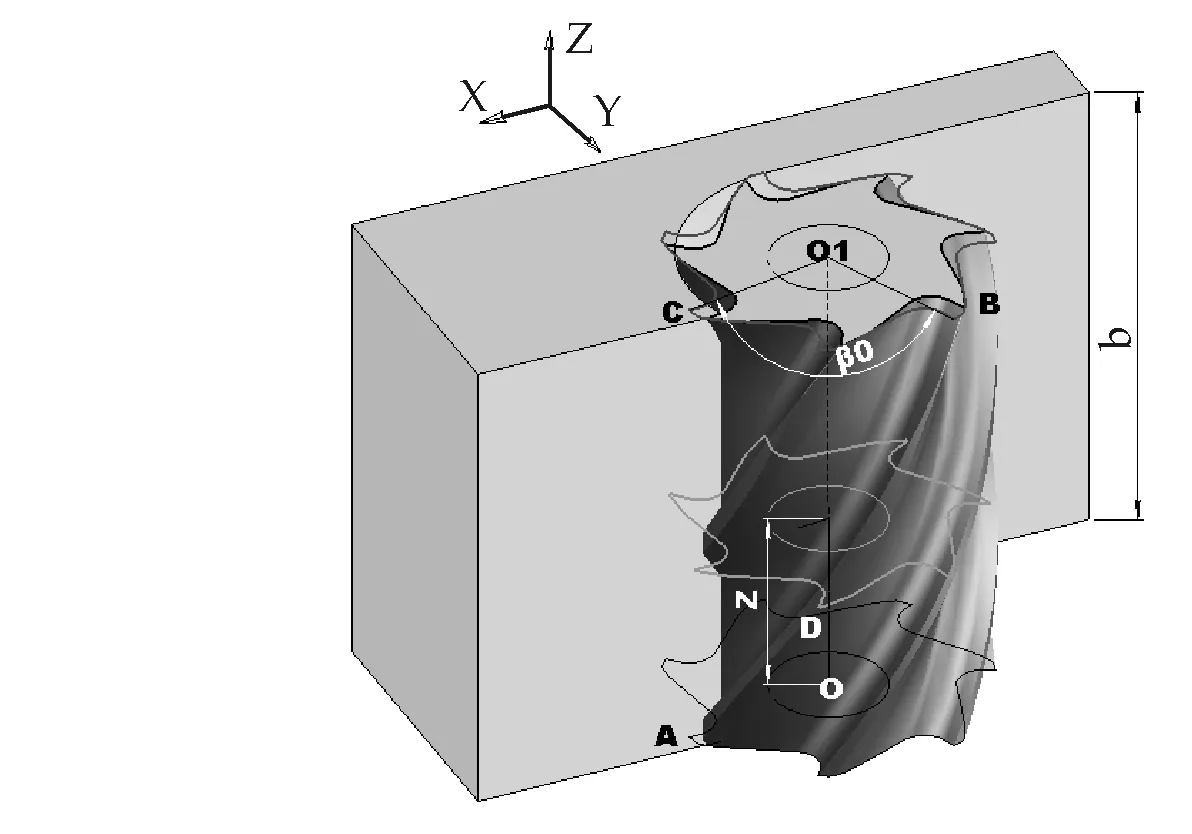
图4 螺旋齿铣削示意图

图5 顺铣时刀齿的受力

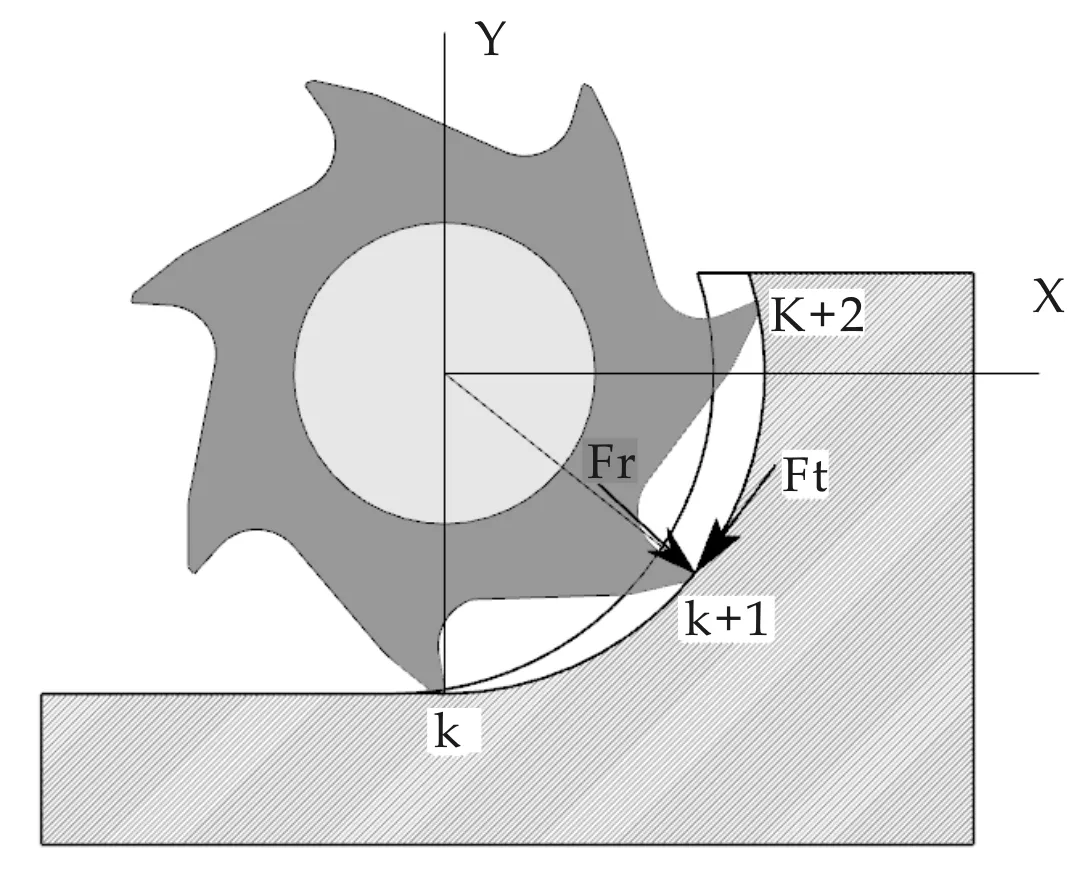
图6 逆铣时刀齿的受力

铣刀为图4的螺旋齿时，齿刃从A至B将在不同的主轴转角时切出工件，在径向(Y)最浅切削厚度处形成倾斜的齿痕，不考虑刀具和工件的变形时，每个刀齿铣出的齿痕是相同的；当考虑刀具的弯曲变形时，铣出齿痕的高度发生变化.顺铣时切削合力方向远离加工表面，合力沿Y轴正方向，由于刀具弯曲使切削厚度减小，刀齿尖点切出的瞬间形成加工表面，如图5所示.逆铣时正好与此趋势相反，切削合力方向指向加工表面方向，合力沿Y轴负方向，由于刀具弯曲使切削厚度增加，刀齿尖点切入的瞬间形成加工表面，如图6所示.在轴向切深方向，顺铣时由于铣刀朝离开切削表面的方向弯曲，而且这种弯曲趋势不会受到任何限制，加工过程是自由的，其切削颤振现象主要由切削力的周期性变化造成.图7中分别标出了现切削刀齿K的理论切削面和实际切削面，前切削刀齿K-1的实际切削面，后切削刀齿K+1的理论切削面和实际切削面，A，B，C，D，E分别是交点.

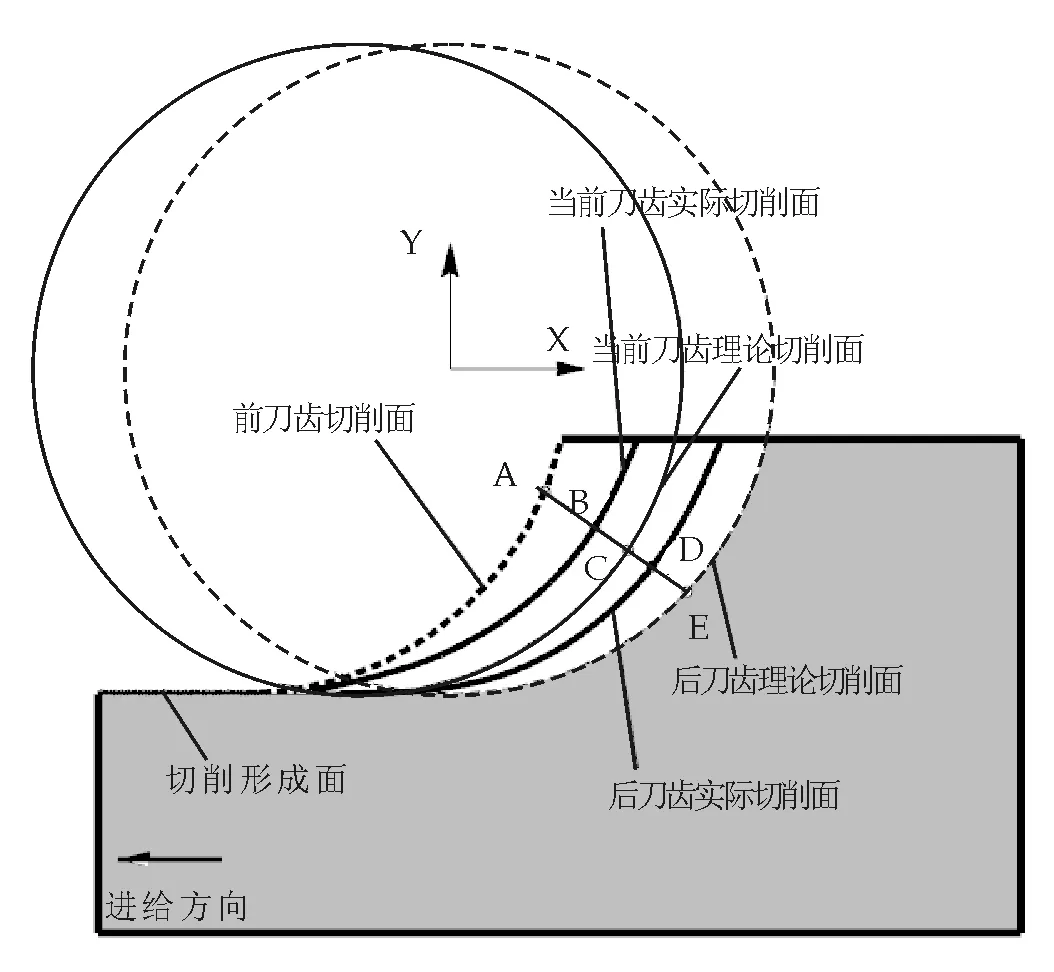
图7 顺铣时由于刀具变形引起的切削厚度变化

假设开始铣削的刀齿面为理论切削面(图7中前刀齿切削面所指的虚线)，在切削力作用下，由于弹性效应刀具发生弯曲，从而使后刀齿的实际切削面前移，形成B点所在的当前刀齿实际切削面，因此K刀齿的切削面积小于理论切削面积，当K+1齿到位进行切削时，在刀具不发生弯曲的情况下，理论上刀齿的轨迹在E点所在的后刀齿理论切削面上，如图7所示，刀齿的虚切削厚度为BE，大于理论切削厚度CE，虚切削力增大，使刀具产生更大弯曲，形成D处的后刀齿实际切削面.后一切削面的形成都是在当前实际切削面基础上计算的，因此顺铣中的欠切现象使每次切削形成的实际切削面逐步远离理论切削面，但这种趋势的变化不是无限制的，当累积变形使某刀齿的虚切削厚度增大到一定程度，计算的实际切削面跨越了前刀齿的理论切削面，因而造成当前刀齿并不能切削材料，使齿的咬合出现打滑现象，简要分析切削中的逻辑关系.

约定刀齿K的理论切削厚度用记号hk表示，实际切削厚度用记号hk′表示，刀杆弯曲变形量用uk表示.图7中当前齿的理论切削厚度(即不考虑刀杆弯曲时的切削厚度)为AC，实际切削厚度AB，刀杆弯曲变形量BC，这一过程的演变逻辑关系为：切削厚度AC产生切削力，切削力的存在使刀杆发生弯曲，刀杆的弯曲使切削厚度减小，减小的切削厚度产生减小的切削力，经过震荡循环使实际切削面最终偏移到图7中B位置.对于低速切削，这一过程循环最终使实际切削力、刀杆变形、实际切削厚度达到平衡状态；高速切削时，若平衡振荡的传播速度低于切削速度，最终只能取得准平衡状态，同样的切削参数下，实际切削厚度小于低速切削情形，切削力也会减小.

若考虑变形的影响，瞬时铣削力的计算非常复杂，每个齿的铣削厚度都是变化的，铣削厚度的变化引起铣削力的变化，铣削力的变化引起变形量的变化，而变形量的变化最终又导致铣削厚度的变化，因此，铣削厚度和弯曲变形是相互影响、相互制约的，是系统内部的一种相互作用，是产生自激振动的根本原因.因此，由于刀具的弯曲，在铣削加工框类零件时，铣出的表面从上而下是倾斜的，在高度方向残留厚度不一致，造成零件加工误差.顺铣条件下，上部铣掉的材料多，下部铣掉的材料少，加工后零件的壁厚上薄下厚，一般上下都大于零件的理论壁厚，因此加工完后对壁厚找正时，应将上部壁厚为基准进行找正；逆铣时与此相反，加工后零件的壁厚上厚下薄，一般上下都小于零件理论壁厚.

3 铣削加工薄壁框类零件时的表面质量

铣削薄壁深腔框类零件时，在铣削力作用下，刀具及框类零件的薄壁结构发生挠曲，出现欠切与过切，顺铣时在径向铣削力作用下，变形的方向相反，刀具与框壁相斥，从而使铣削量不足造成欠切现象；逆铣时变形的方向相对，刀具与框壁相吸，使铣削量加大造成过切现象.图8,图9分别是顺铣和逆铣薄壁零件时铣刀与壁板的弯曲示意.

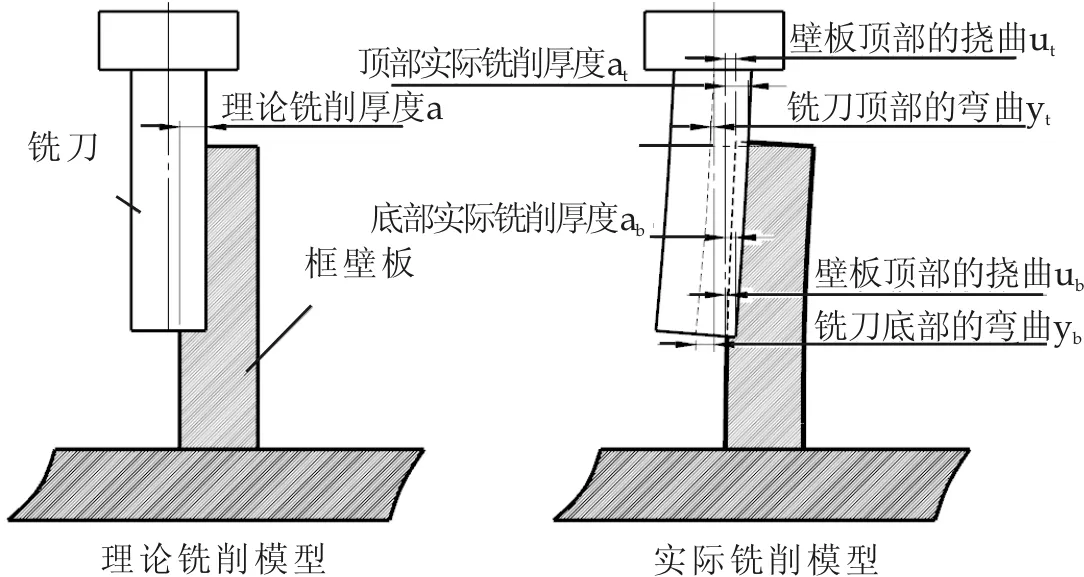
图8 顺铣薄壁零件时铣刀与壁板的弯曲变形

图9 逆铣薄壁零件时铣刀与壁板的弯曲变形

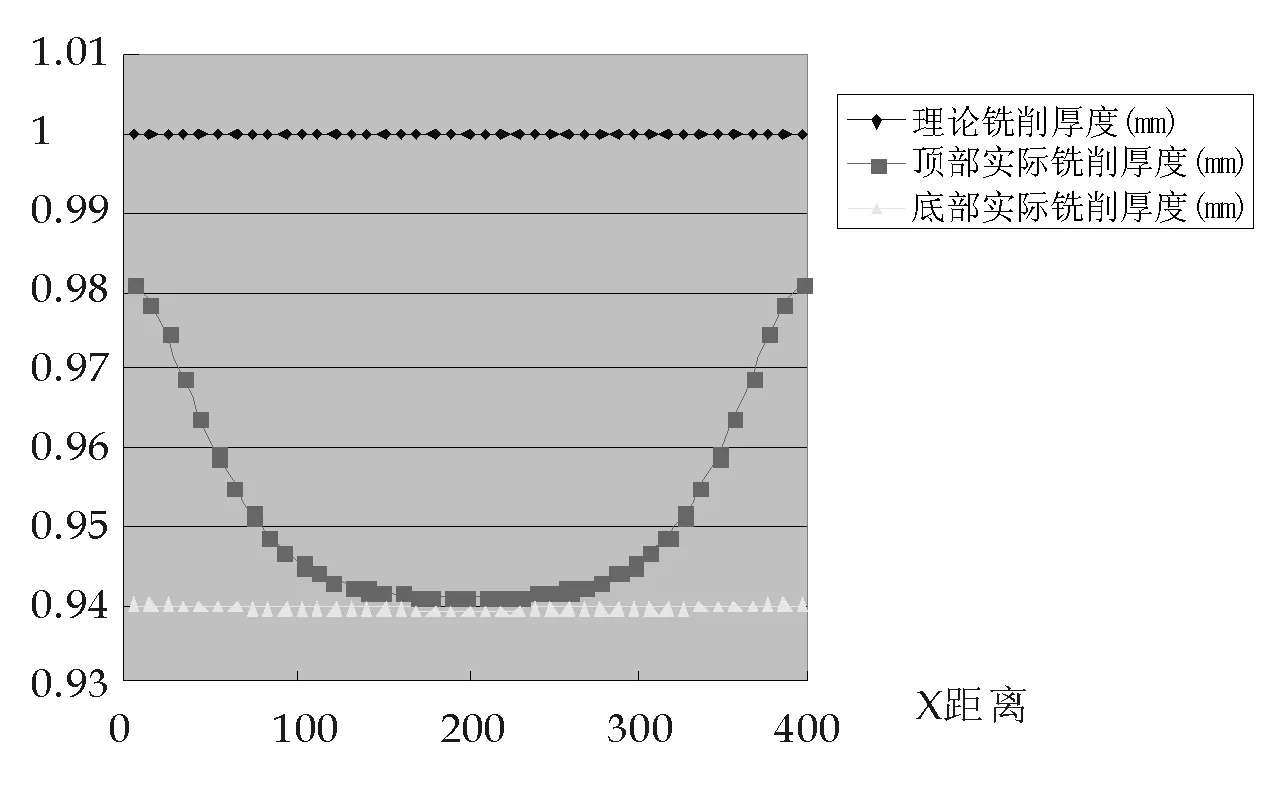
壁板的挠曲和铣刀的弯曲参数如图8、图9中所表示，满足以下关系.

顺铣时实际铣削厚度：

at=a-(yt+ut)

ab=a-(yb+ub) (1)

逆铣时实际铣削厚度：

at=a+(yt+ut)

ab=a+(yb+ub) (2)

式中a为理论铣削厚度，yt,yb分别是铣刀顶部、底部的弯曲变形；ut,ub分别是壁板顶部、底部的挠曲变形.如果框壁的刚度足够强， 部分可忽略.在航空类零件中，有些结构件的框壁很薄，小到甚至只有几毫米，在铣削这类零件时，壁板的挠曲变形是主要部分.顺铣时由于铣削力使壁板的弯曲趋向自由的一面，若铣削力过大时壁板可能会丧失稳定性，需要验证铣削这类零件的稳定极限载荷；逆铣时由于刀具与壁板之间的相互吸引，壁板不会发生失稳现象，铣削很薄的壁板类零件建议采用逆铣方式.

采用有限元法编程依次计算任意加工点处刀具及壁板的刚度，在此基础上推导铣削薄壁框类零件时厚度偏差的计算，程序同样适用于多框零件.

11段和13段两句What if条件问句的使用，目的在于改变读者对怪物的看法。即便他自负，即便他对生活不忠，这都不重要，重要的是他是个伟大的天才，是不可多得的人物。他没时间去过正常人的生活也不足为奇。

3.1 极限铣削力

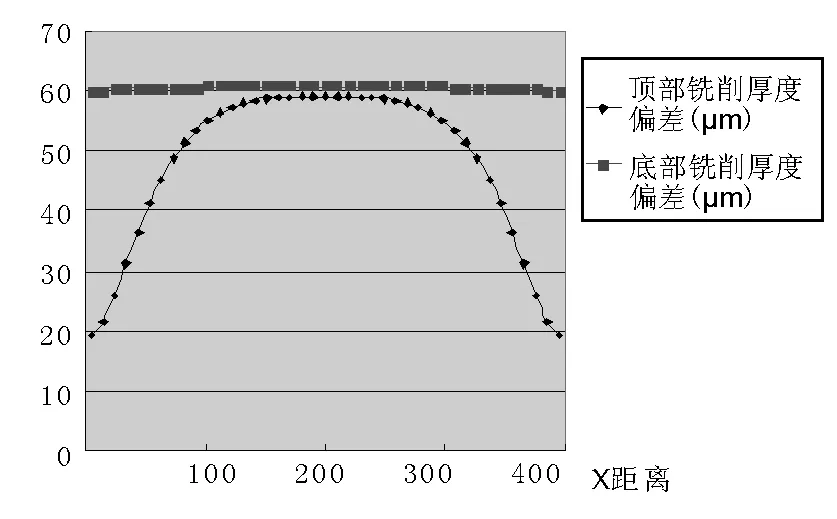
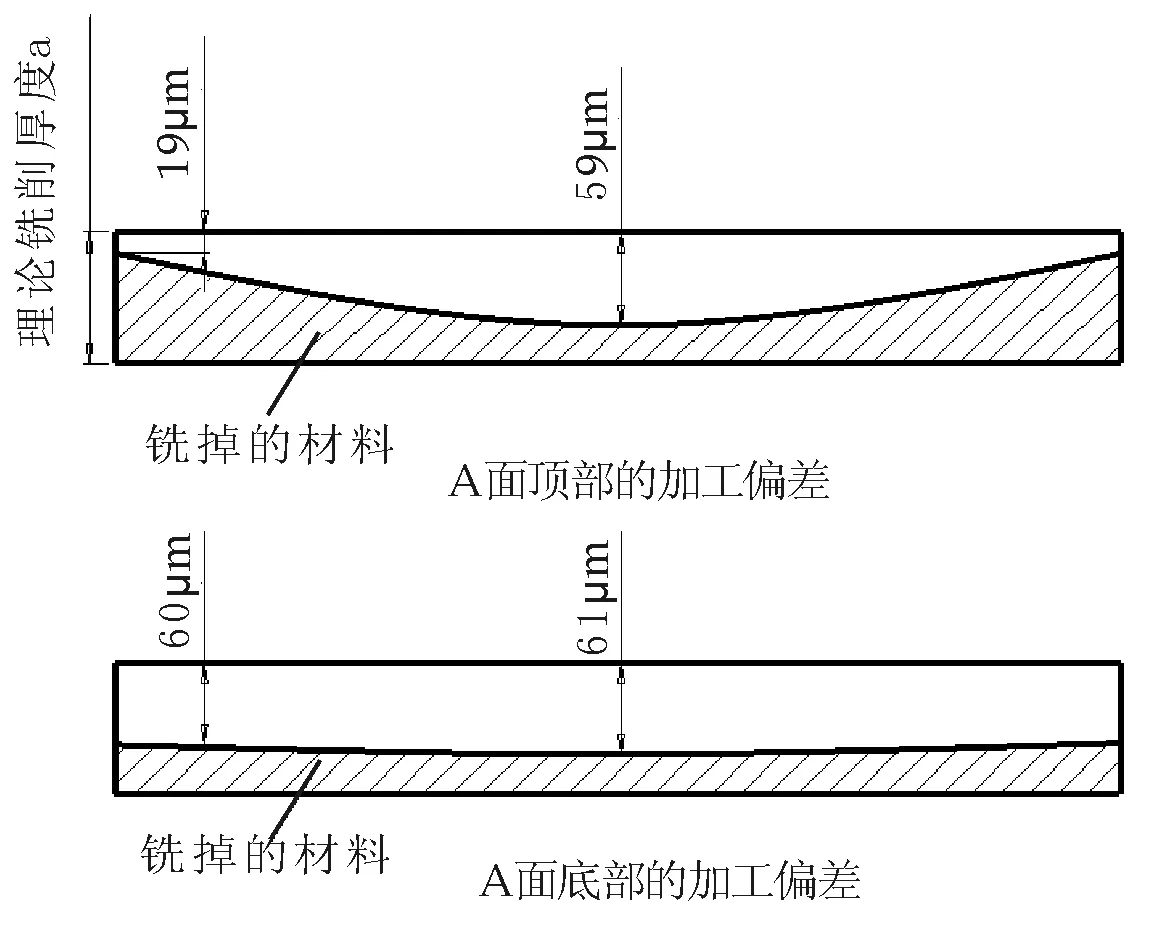
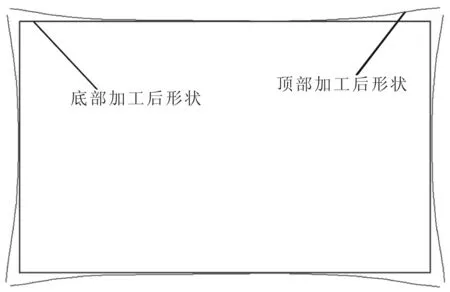
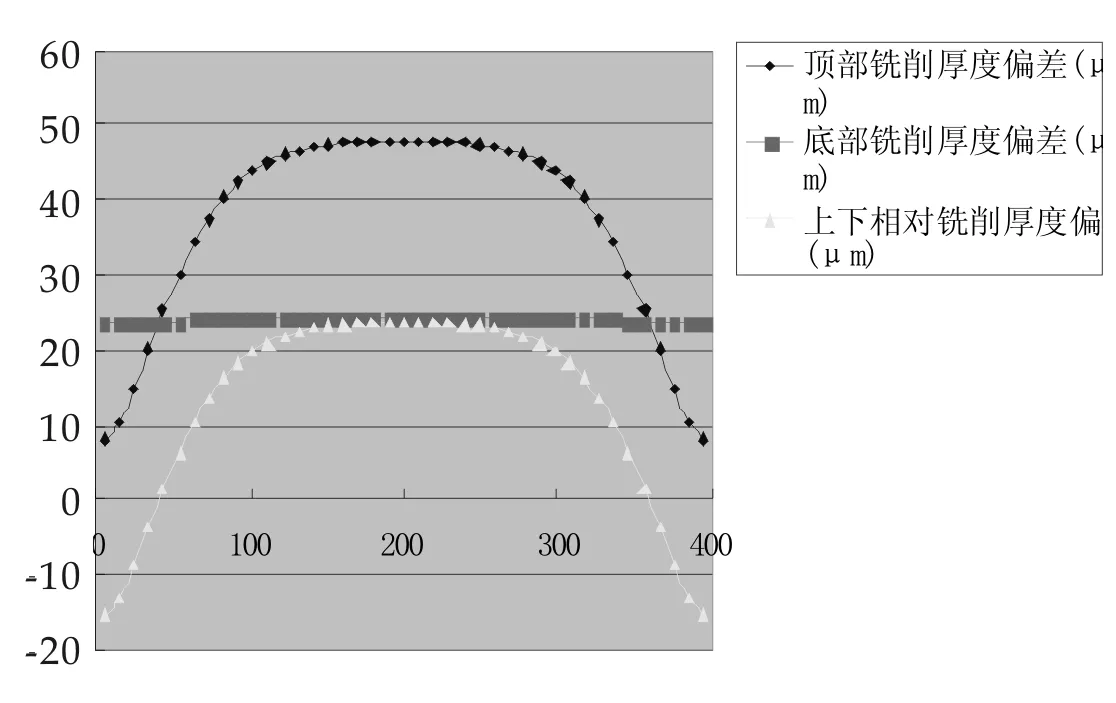
在顺铣厚度的计算公式(1)中，yb>yt,ub

刀具与壁板的变形量yt,yb,ut,ub都是径向铣削力fy的函数，且随fy的增加呈现增长的趋势，当fy增加到使铣削厚度apj等于0时，铣削力达到极大值，此时若再增大铣削量，刀具与壁板将出现打滑现象，铣削过程不能进行下去.对于确定的刀具和铣削结构件，通过上述关系可确定出极限铣削力fΘ：

yt(fΘ)+yb(fΘ)+ut(fΘ)+ub(fΘ)=2a(3)

通过有限元法，将框类零件划分为微小单元结构，用循环计算的方法得到任意加工位置壁板的挠曲刚度，公式(3)中的ut(fΘ),ub(fΘ)用挠曲刚度表达为：

ut(fΘ)=fΘ/kkt

ub(fΘ)=fΘ/kkb

kkt,kkb为当前铣削位置顶部与底部的挠曲刚度，为加工零件尺寸和材料参数的函数，通过有限元法可得到.根据对铣刀弯曲计算的推导，铣刀顶部与底部的弯曲为：

式中b为轴向铣削深度，L为铣刀长度，kDt,kDb为铣刀顶部与底部的弯曲刚度，为刀具半径、刀具长度和刀具材料参数的函数：

因此由(3)得到径向极限铣削力：

铣削图10的铝合金框零件时，周边壁厚5mm，沿A,B面顺铣，框轴向铣削深度70 mm，采用的铣刀长度130 mm,半径7.5mm,齿数6，螺旋角30度，刀具材料的弹性模量240 GPa，在该加工参数下径向铣削力为80 N，铣削力作用下壁板某位置挠曲如图11.显然，当加工点位于A，B面的中间时，壁板的挠曲变形最大，挠曲刚度最小.

图10 铣削铝合金框的模型参数

图11 铣削壁板某位置时的挠曲

在框零件A面壁板中间位置处的挠曲刚度：

kkt=80/0.040 302=1985 (N/mm)

kkb=80/0.001 008=79 365 (N/mm)

得铣削A面的极限铣削力：

在框零件B面的中间壁板的挠曲刚度：

kkt=80/0.037 624=2126 (N/mm)

kkb=80/0.000 930=86 021 (N/mm)

得铣削B面的极限铣削力：

极限铣削力是径向铣削厚度a的函数，铣削厚度越大，极限力越大.该框计算结果表明，刀具弯曲刚度小于壁板挠曲刚度，所以刀具相对来说偏软，加工变形主要由刀具弯曲部分产生.在其它铣削参数确定的情况下，铣削力是进给量和径向切削厚度的函数.因此当进给量和径向切削厚度分别给定时，由极限铣削力可确定另一个铣削参数的极限值.当径向切削厚度取1mm时，顺铣加工该框零件的每齿进给量不能超过0.6mm.

3.2 零件铣削壁厚偏差

采用有限元法计算多框零件壁板在任意加工点的挠曲刚度Kb，刀具对应铣削位置的弯曲刚度Kd，对于一组确定的加工参数，计算出加工到该位置时的径向铣削力fy，得到铣削力作用下的壁板挠曲量us以及刀具的弯曲变形量ys，顺铣时由公式(1)得到该点实际铣削厚度as：

as=a-(ys+us)=a-fy×(1/Kb+1/Kd)

该点铣削厚度偏差ps：

ps=ys+us=fy/Kb+fy/Kd

壁厚加工偏差是刀具弯曲和壁板挠曲共同作用影响的结果，刚度越大影响越小，为获得高精度的计算结果，有限元网格需划分密一些.从计算公式看出，为减小加工偏差，一种措施是减小铣削力的值，另一措施是增加刀具和壁板的刚度.当壁板和刀具刚度相差很大时，加工偏差主要由刚度低的一方造成，刀具刚度较容易获得保证，可通过加大刀具半径、减小悬伸来增加刀具刚度.提高壁板的刚性要困难得多，一般只能采用分层铣削方式解决.

4 数值算例

采用长度为130 mm,半径7.5mm,齿数6，螺旋角30度的铣刀铣削图10的铝框，框周边壁厚5mm， A面的铣削加工计算结果如图12～图15所示.

加工A面时，顶部最大铣削厚度偏差在壁板中间位置，为59μm，最小铣削厚度偏差在壁板两边，为19μm；底部最大铣削厚度偏差在壁板中间位置，为61μm，最小铣削厚度偏差在壁板两边，为60μm，因此A面上下最大铣削偏差为41μm.因为铣刀的刚度低于壁板的刚度，适当增加铣刀半径可减小壁板的加工偏差.

将铣刀半径增大到9.5mm，其它参数保持不变，计算框的加工偏差，得到A面的铣削加工计算结果如图16，图17所示.加工A面时顶部最大铣削厚度偏差为48μm，底部最大铣削厚度偏差为24μm，A面上下最大铣削偏差为24μm.通过加大铣刀半径，较大幅度提高了铣削面的加工质量.

图12 壁板A实际铣削厚度曲线

图13 壁板A铣削厚度偏差曲线

图14 壁板A顶部和底部的铣削厚度偏差示意

图15 加工完成后框内壁的形状

图16 铣刀半径加大后壁板A铣削厚度偏差

图17 铣刀半径加大后加工完成的框内壁的形状

5 结论

铣削薄壁深腔框类零件时，在铣削力作用下刀具及框类零件的薄壁结构发生挠曲，出现欠切与过切，从而使加工厚度产生偏差.顺铣时变形方向相反，刀具与框壁相斥，从而使铣削量不足造成欠切现象；逆铣时变形方向相对，刀具与框壁相吸，使铣削量加大造成过切现象.顺铣时由于铣削力使壁板的弯曲趋向自由的一面，因此若铣削力过大时壁板可能会丧失稳定性；逆铣时由于刀具与壁板之间相互吸引，壁板不会发生失稳现象，因此铣削很薄的壁板类零件时，建议采用逆铣方式.采用有限元法，综合考虑刀具与壁板变形，得到铣削薄壁框类零件的铣削厚度偏差，通过数值算例研究减小加工偏差的方法，从而提高航空薄壁零件加工精度.

[1] 陈 勇,刘雄伟,俞铁岳.立铣加工切削力和振动的计算机仿真与实验[J].华侨大学学报(自然科学版),2006,27(1):71-75.

[2] 汪文津,王太勇,范胜波,等.车削过程切削力的计算机数值仿真[J].机械强度,2006,28(5):725-728.

[3] Yusuf Altintas著,罗学科译.数控技术与制造自动化[M].北京：化学工业出版社,2002：3-192.

[4] 康永刚,王仲奇,吴建军,等.立铣切削力分类研究及精确铣削力模型的建立[J].航空学报,2007，28(2):481-489.

[5] Kline W. A,Devor R E,Lindberg R. The prediction of cutting forces in end milling with application to cornering cuts[J]. International Journal of Machine Tool Design and Research， 1982 ,22 (1) :7222.

[6] Ehmann K. F, Kapoor S. G, Devor R E. Machining process modeling a review[J]. ASME Journal of Manufac-turing Science and Engineering,1997，(119):655-663.