Response Surface Optimization for Process Parameters of LiFePO4/C Preparation by Carbothermal Reduction Technology*

YANG Kedi (杨克迪), TAN Fangxiang (谭芳香), WANG Fan (王凡), LONG Yunfei (龙云飞)and WEN Yanxuan (文衍宣)**

School of Chemistry and Chemical Engineering, Guangxi University, Nanning 530004, China

1 INTRODUCTION

LiFePO4with olivine structure has been intensively studied as a potential cathode material for next generation of Li-ion batteries [1, 2] due to its stable structure and safety. However, the coarse LiFePO4particles have poor rate performance for its low electronic and lithium-ionic conductivity [3, 4]. To improve the rate performance of LiFePO4electrode, following methods have been proposed: (1) surface coating with conductive material to improve the electronic conductivity [5-9]; (2) doping with guest ions to increase the diffusion rate of Li+ions [10, 11]; and (3)minimizing the particle size to shorten the bulk diffusion distance of Li+ions [12, 13].

Various methods have been reported for the synthesis of LiFePO4cathode material [4], including solid-state reaction [2], mechano-chemical activation[8, 14, 15], carbothermal reduction technology (CRT)[16-25], hydrothermal processing [26], sol-gel processing [27], and precipitation method [28]. Among these methods, CRT possesses some prominent characteristics, such as cheap precursors, simple synthesis process and large mass production. In addition, the residual carbon introduced by reductive additive in CRT provides better electron transport in the composite electrode and impedes the growth of LiFePO4particles size, which can effectively enhance the electrochemical performance of LiFePO4.

The synthesis of LiFePO4cathode material via CRT method usually uses Fe2O3[16, 21] or FePO4[17-20, 22-26] as Fe (III) precursors, and carbon [16, 18, 21],polymer [17, 19], organic acid [20, 24], glucose [21, 22, 25]and sucrose [23] as reductive agent. Sucrose, as a renewable and non-hazardous reducing agent, has its advantages of low cost and rich resource. In the present work, sucrose is also used as effective carbon precursor for the synthesis of high-performance LiFePO4/C composite material [6, 8, 15, 23].

Among the numerous parameters, sintering temperature, sintering time and amount of reductive agent are the keys to determine the electrochemical performance of LiFePO4synthesized by CRT method[16-25]. These parameters have been examined by the conventional one variable at a time approach (OVAT),in which the effect of each experimental factor is investigated by changing one factor at a time while keeping other factors constant. However, this method is not only time and work demanding, but also lacks of considering the effect of interaction between factors.Thus it is necessary to find a multivariate statistic technique to optimize the preparation processes of LiFePO4by CRT.

Response surface methodology (RSM), as a statistically based optimization strategy, is useful to explore the effects of several independent variables [29].The main advantage of RSM is the reduced number of experimental trials needed to evaluate the multiple parameters and their interactions [29, 30, 31]. Although it has been proved that RSM is a powerful statistical tool to deal with multivariate experimental design strategy in process optimization [30, 32-36], there are few studies to optimize the carbothermal reduction synthesis of LiFePO4/C by the RSM approach.

In the present work, we focus on the optimization of the reductive process parameters of LiFePO4/C prepared by CRT using LiOH, inexpensive FePO4and sucrose as raw materials. The sintering temperature,sintering time and carbon content (the mass of sucrose for preparing 1 mol LiFePO4) are determined as the main influencing factors in the experiments. The discharge capacity of LiFePO4/C is selected as the response affected by these variables. The central composite rotatable design (CCD) is used to study the effects of the three variables on the response. RSM is applied to determine the optimal condition and an empirical model correlating the discharge capacity to the three variables is developed.

2 MATERIALS AND METHODS

2.1 Experimental design and analysis

Based on previous work [16-25], three reaction factors, sintering temperature (X1, °C), sintering time(X2, h) and carbon content (X3, g·mol-1), are considered as the independent variables. The dependent variables are the discharge capacity (Y, mA·h·g-1) and the capacity retention ratio (R, %) of LiFePO4/C.

RSM is an empirical statistical technique employed for multiple regression analysis by using the data from properly designed experiments to solve multivariate equations simultaneously [29, 30, 32-34].In this work, RSM is used to assess the relationship between the response (YorR) and independent variables, as well as optimize the values of variables in order to predict the best response.

Central composite rotatable design (CCD) is the most widely used approach in RSM. According to Guvenet al. [30], CCD is an effective design for sequential experimentation, since it allows reasonable amount of information to test the lack-of-fit with a sufficient number of experimental values. Therefore,CCD is applied to determine the effect of operational variables on the discharge capacity in this work. The three-factor layout of the CCD is shown in Fig. 1. By defining the distance from the center of the design space to a factorial point as ±1 unit for each factor, the distance from the center to axial (star) points is ±α(|α|＞1) [29, 31]. It is composed of a core factorial that forms a cube with sides that are two coded units in length (from -1 to +1 as noted in Fig. 1).

The coded variables and actual variables for CCD are shown in Tables 1 and 2. The relationship between coded variables and actual variables can be expressed as [29]

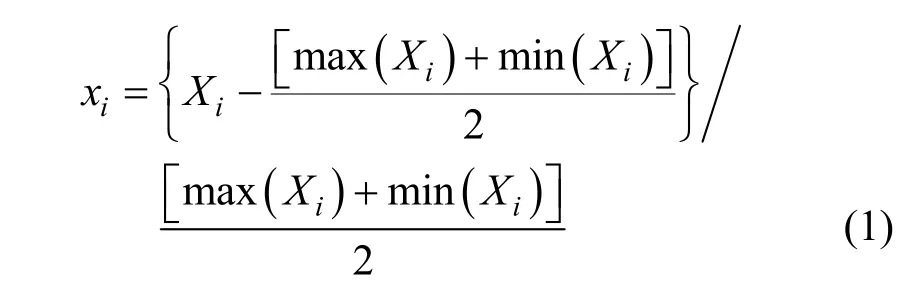
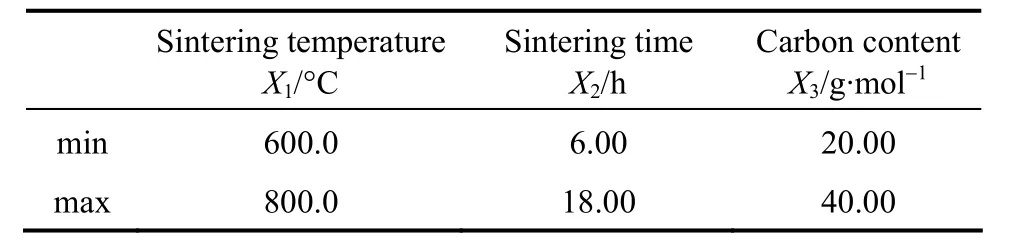
Table 1 Levels of independent variables for CCD

Each numeric factor is varied over 5 levels in the determined ranges based on preliminary experiments.The conventional choice for the CCD is to execute a rotatable design with the axial points at |α|=1.682 coded units from the center. As a result, the total number of the experiment in this design is calculated as 20 (=2k+2k+6), wherekis the number of factors(k=3). Meanwhile, 8 factorial points, 6 axial points and 6 replications of the central points are added to check the fitting degree of the model.

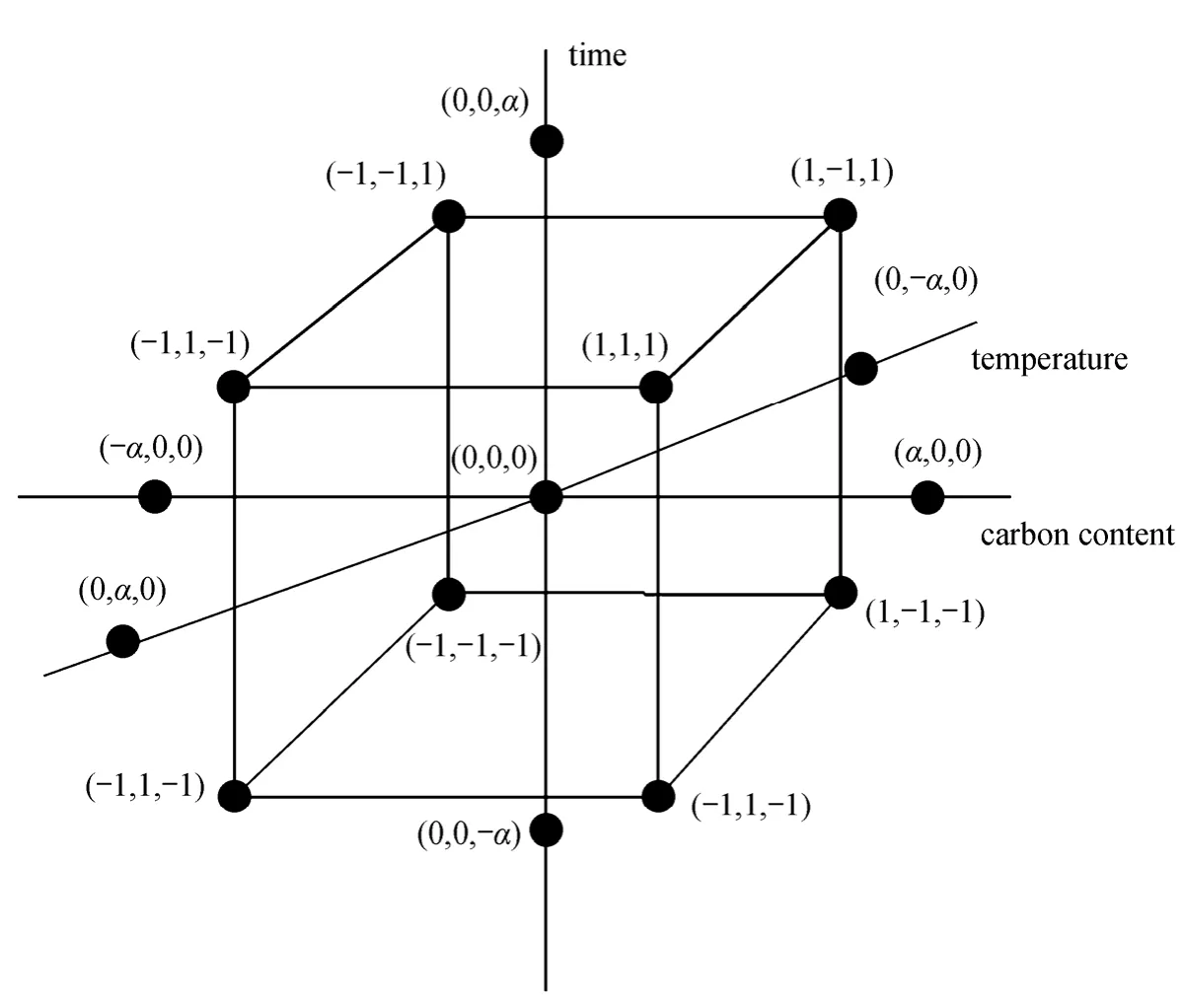
Figure 1 Central composite design with three operating conditions

Table 2 Coded variables and actual variables for CCD

The discharge capacity (Y, mA·h·g-1) and the capacity retention ratio (R, %) of LiFePO4/C influenced by three independent variables are set as the desired goal (response) for fitting a second-order polynomial regression model:

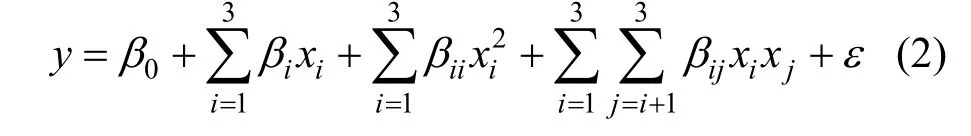
whereyis the predicted response ofYorR,β0is the coefficient for the intercept,βiis the coefficient of linear effect,βiiis the coefficient of quadratic effect,βijis the coefficient of interactive effect,εis a term representing other sources of variability not accounted by the response function, andxiandxjare coded independent variables. The quality of the fitness of polynomial model is expressed by the value of correlation coefficient (R2). The main indicators demonstrating the significance and adequacy of the model include the F-value (Fisher variation ratio), P-value(probability value), and adequate precision [35]. The consideration of multiple responses involves the initial creation of suitable response surface model and subsequent identification for the operational conditions that maximize targeted response or maintenance of those in the most desired ranges [35].

2.2 Experiments

To synthesize LiFePO4/C material, FePO4·2H2O and LiOH·H2O (AR, Beijing Chemical Reagent Co.)at a molar ratio Li/Fe of 1.00∶1.00 were thoroughly mixed with sucrose in a planetary mill (QM-ISP4),and then dried at room temperature in air. The mixture was transferred to a tube furnace, sintered in the atmosphere of nitrogen in different processes. The LiFePO4/C product was obtained after cooling.

The phase composition and structure of the products were identified by X-ray diffraction (XRD,Rigaku D/MAX2500V diffractometer with Cu Kαradiation). The morphologies of powder were observed with scanning electron microscope (SEM, Hitachi S-3400N) and transmission electron microscope(TEM, JEM-1200EX).

Electrochemical characteristics of products were studied using CR2032 coin-type cell. The chargedischarge tests for the cells were performed on a CTA2001 battery testing system (Wuhan, China) between 2.5 and 4.2 V (vs. Li/Li+) with different current densities, and 1 C rate was 170 mAh·g-1. Current densities and specific capacities were calculated based on the mass of LiFePO4/C in the electrode. Slurry was formed by mixing LiFePO4/C, acetylene black and Polyvinylidene Fluoride (PVDF) binder with a mass ratio of 80∶10∶10. The mixed slurry was coated to an aluminum current collector. After being dried under vacuum at 120 °C for 12 h, the electrodes were punched and weighed. The electrochemical cells were assembled in a glove box under a dry and high purity argon atmosphere. The complete coin cell comprises a cathode, a Celegard 2300 as the separator, and lithium foil anode. 1 mol·L-1LiPF6 dissolved in a mixture of ethylene carbonate and dimethyl carbonate (1∶1 by volume) was used as the electrolyte.

3 RESULTS AND DISCUSSION

3.1 Response analysis

A total of 20 runs of the CCD experiment responses are shown in Table 3. The experimental discharge capacity at 0.5 C varies between 76.3 and 147.6 mA·h·g-1, while the capacity retention ratio varies between 60.1% and 100.6%, revealing that the sample with high discharge capacity has good capacity retention ratio. Thus, the discharge capacity is selected as the response variable in subsequent investigations.

Further, the numerically analysis of the response results (Table 3) is shown in Table 4. The cubic model is not considered to fit the response since the central composite design cannot support a full cubic model and not all the cubic model parameters can be uniquely estimated. Instead, according to the sequential model sum of squares and lack-of-fit tests, the model with the highest order polynomial is selected if the additional terms are significant and the model is not aliased and has insignificant lack-of-fit. The lack-of-fit error is significantly larger than the pure error, indicating that something remained in the residuals can be removed by a more appropriate model.In addition, significant lack-of-fit (the P-value is 0.10 or smaller) indicates that the model can not be used as a predictor of the response. Since the lack-of-fit is not desirable, an appropriate F-value larger than 0.1 are in need. Herein, the quadratic model offers a lack-of-fit F-value of 1.3 with P-value of 0.4, and the quadratic terms with P-value are less than 0.0001, and the linear terms with P-value are less than 0.1, meaning appropriate polynomial models for the selected response.

Table 4 also shows the model fitting for the selected response. Both the R-squared and related adjusted R-squared statistics should be close to 1. Actually, 98%of the variation in the observed values can be explained with the chosen model. The predicting residual error sum of squares (PRESS) indicates the fitness of model to the data. The PRESS for the chosen model should be smaller than that of other models to be chosen.The model summary statistics shows the standard deviation (Std. Dev.), the R-squared and adjusted R-squared,predicted R-squared and PRESS statistics for each complete model. Low standard deviation, R-squared value closes to 1 and low PRESS is better. As showed in Table 4, for the quadratic model, R-squared (0.99)and related adjusted R-squared (0.98) are close to 1 and the PRESS of 738.03 is small enough, farther supportting the selection of the quadratic model.

Table 3 Central composite design arrangement and results

Table 4 Model fitting for the designed experiments (the selected response)

Table 5 Analysis of variance (ANOVA) for response surface quadratic model

The ANOVA analysis by multiple regression using P-values was also performed for determination of the constants, coefficients of linear, quadratic and interaction effects. The results of quadratic model for the discharge capacity are listed in Table 5. The P-value greater than 0.1 indicates that the model terms are not significant, while this value less than 0.0500 indicates significant model terms. The small P-value (＜0.0001)and large F-value (=94.7) implie that the quadratic model is significant. In this case,x1,x3,x1x2,x1x3,x2x3,x12andx32are significant model terms. Among the three independent variables tested, temperature (P-value＜0.0001) and carbon content (P-value＜0.0001) have significant linear effects and quadratic effects on initial discharge capacity. Sintering time also shows a negative quadratic effect on initial discharge capacity,with a relatively smaller linear effect. However, interaction effects of sintering time with temperature or carbon content are both important. The effect on initial discharge capacity of three factors isx1＞x3＞x2.

The lack-of-fit F-value of 1.3 implies that it is not significant relative to the pure error. 39.4% chance of the lack-of-fit F-value becomes significant due to the exact replicate values of the independent variable in the model, which provide an estimate of the pure error. According to Myerset al. [29] and Joglekar and May [34], for a good fitness of a model, the correlation coefficient should be at a minimum of 0.80. For the quadratic model, the predicted R-squared value of 0.94 is in reasonable agreement with the adjusted R-squared value of 0.98 (Table 4). The adequate precision measures the signal to noise ratio and a value greater than 4 is desirable. The ratio of 25.4 indicates an adequate signal. Hence, the model can be used to navigate the design space.

The values of fitting coefficients in Eq. (2) are shown in Table 6. The equation in terms of coded factors is obtained:

According to Eqs. (1) and (3), the final equation in terms of actual factors is:

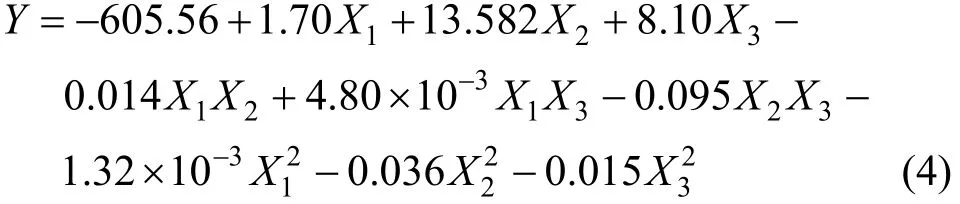
It is important to confirm that the selected model provides adequate approximation to the real system.By using the diagnostic plots, including normal probability plots of the studentized residuals and the plots of predictionversusactual value, the model adequacy can be judged [35].

Figure 2 shows the normal probability plot of studentized residual for initial discharge capacity. The residuals follow a normal distribution and the pointsfollow a straight line, so that the model is valid.

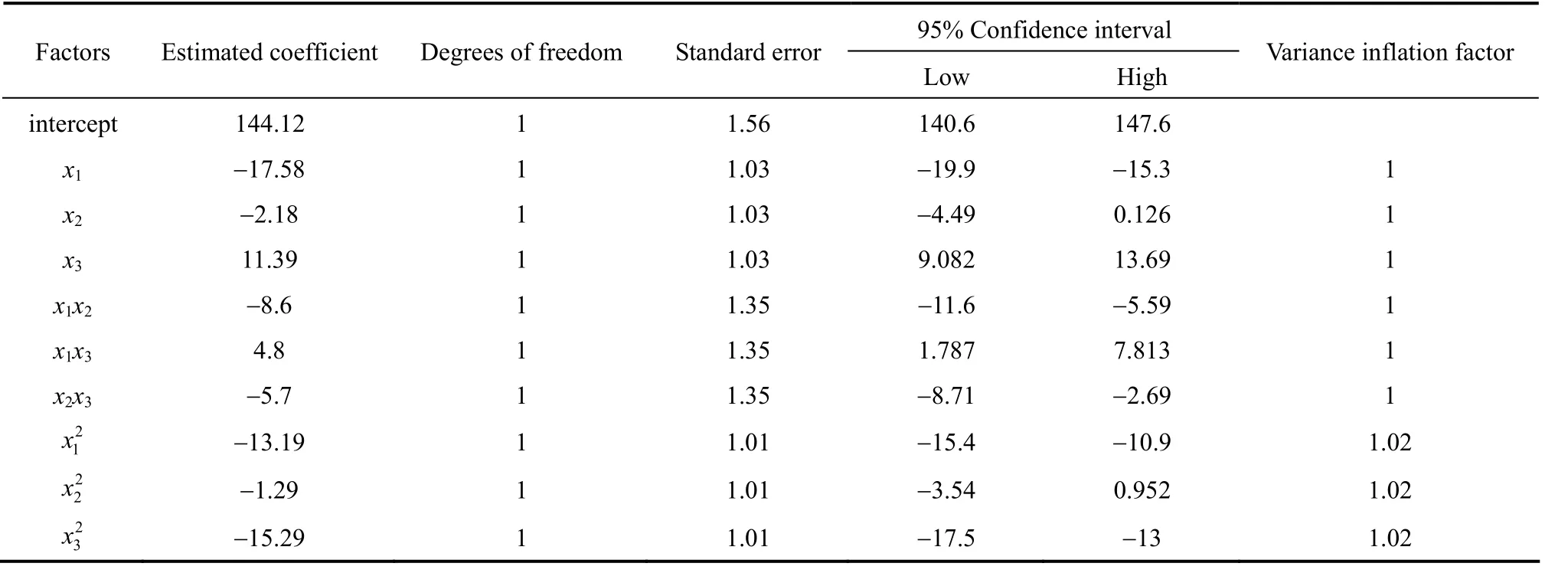
Table 6 Regression coefficients for refitted model

Figure 2 Normal probability plot of studentized residual

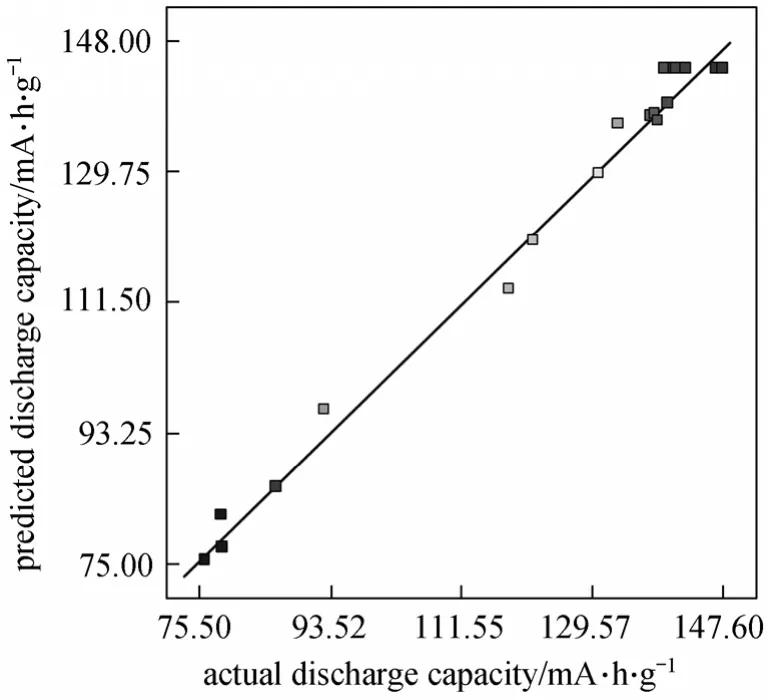
Figure 3 Goodness-of-fit of empirical model

Experimental resultsversuspredicted values obtained by the refitted model for the discharge capacity are showed in Table 3 and Fig. 3. Actual response values are the data for a particular run, and the predicted response values are evaluated from the model and generated by using the approximating functions.As shown in Fig. 3, the predicted values are in good agreement with the experimental values.

3.2 Response surfaces

To achieve better understanding for the interactions of variables and to determine the optimum level of each variable for the maximum capacity, three-dimensional(3D) response surfaces and contour plots of the relationship betweenx2andx3,x1andx3,x1andx2are illustrated in Fig. 4. The values ofx1,x2andx3hold constant at the central level. The figures are constructed by the Design Expert software and utilized to assess the interactive relationships between independent variables and response. Fig. 4 shows the initial discharge capacity with different sintering time and carbon contents at 700 °C. It is clear that the carbon content have positive effect on the initial discharge capacity. As carbon content increases from 20.0 to 35.0 g·mol-1,the initial discharge capacity increases from 87 to 140 mA·h·g-1. This increase can be easily explained in terms of enhanced electronic conductivity by the introduction of conducting carbon and fine particle sizes by hindering the particle growth during sintering [5-7]. However,the initial discharge capacity only slightly increases with sintering time as carbon content further increases.This may be due to the fact that long sintering time results in a full crystallization. Thus, the effect of time on initial discharge capacity is insignificant.

Figure 5 shows the 3D response surfaces and contour plots as a function of temperature and carbon content, while the sintering time keeps constant (12 h).The initial discharge capacity slightly increases with carbon content when the carbon content is less than 30 g·mol-1, and this increment becomes smaller as temperature increases. This behavior is attributed to the reducing of LiFePO4grain size by the carbon from the pyrolysis of the sucrose in the CRT. The capacity of LiFePO4decreases as the temperature is away from 700 °C. The aggregation at high temperature and the incomplete crystallization at low temperature reduce the capacity of the LiFePO4particles [25].

Figure 6 shows the effect of sintering time and temperature on initial discharge capacity at constant carbon content of 30 g·mol-1. The discharge capacity depends highly on the synthesis temperature, first increases and then decreases between 600 to 800 °C.The lower discharge capacity of LiFePO4/C samples synthesized at temperature below 600 °C should be attributed to the low crystallinity and electronic conductivity of product. However, the abrupt increase of particle size may occur when the temperature is higher than 700.0 °C, lowering the discharge capacity. The initial discharge capacity does not increase significantly with the increase of sintering time, suggesting that the sintering time has less effect. The poor electrochemical performance may be caused by the incomplete crystalline in the short sintering time.

Figure 4 Response surface and contour plots for different sintering time and carbon contents at 700 °C

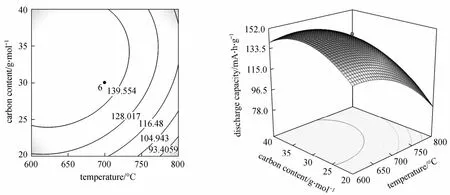
Figure 5 Response surface and contour plots for different temperatures and carbon contents

Figure 6 Response surface and contour plots for different sintering time and temperatures

3.3 Determination of optimum conditions

The purpose of this study is to optimize the three operation parameters (temperature, sintering time and carbon content) that maximize the initial discharge capacity using response surface analysis. After the fitted model is checked for adequacy of fitness in the region defined by the coordinates of the design and is found to be adequate, the model is used to locate the coordinates of the stationary point [29]. Accordingly,the fitted second order model ink-variables is written in matrix notation [29]. By the optimization, the stationary points with actual un-coded variables are given as the following variables: temperature 652.0 °C,sintering time 8.48 h and carbon content 34.33 g·mol-1.The optimal values are located within the limits of the region of interest and varied around the center points to a limited extent in this study.

3.4 Confirmatory experiments

In order to test the validity of the optimum condition achieved by the empirical model, an additional experiment was carried out with the optimized parameters: temperature 652.0 °C, sintering time 8.48 h and carbon content 34.33 g·mol-1. The initial discharge capacity is found to be 147.2 mA·h·g-1, while the value predicted by Eq. (3) is 150.8 mA·h·g-1under this optimum condition, which is consistent with the experiment with a deviation of 1.87%. The model fits the experimental data very well under these experimental conditions.

Figure 7 shows that the main phase of the sample prepared under the optimum conditions can be identified as LiFePO4with an ordered olivine structure indexed to orthorhombic Pnmb (JCPDS: 40-1499) [36].There is no extral diffraction peak associated crystal modification by carbon, due to its amorphous structure and/or low content in the composite, and hence the presence of carbon does not influence the structure of LiFePO4.

Figure 8 shows the SEM and TEM images of LiFePO4/C composites synthesized with the optimal parameters. All the powder synthesized shows less granular and displays similar spherical morphology with a uniform dispersion. The LiFePO4/C powder is mainly fine particles between 50-100 nm in size, with a few large particles or agglomerates with sizes less than 1 μm. There is no remarkable segregation of carbon in the mapping area, which indicates the nano-sized carbon particles are uniformly coated on the surface of LiFePO4powder. Compared with the LiFePO4compounds synthesized by conventional solid-state reaction [37-40], the fine size obtained here indicates that thein-situcoating of carbon from the sucrose on the surfaces of LiFePO4particles effectively inhibits the growth of particle.

Figure 9 presents the rate performance of LiFePO4/C composites synthesized under the optimum conditions.The electrode of LiFePO4/C shows a cycling capacity as high as 147.2 mA·h·g-1and a discharge voltage of 3.37 V, implying the two-phase redox reaction between FePO4and LiFePO4[2] at 0.5 C. The discharge capacities are 149.7, 147.2, 123.8 and 105.1 mA·h·g-1at 0.2 C, 0.5 C, 2.0 C and 5.0 C, respectively. It is still in good stability and reversibility after 50 cycles.

Figure 7 XRD pattern of the LiFePO4/C powder prepared

Figure 8 SEM and TEM images of the as-prepared LiFePO4/C powder

Figure 9 The performance of the as-prepared LiFePO4/C1—0.2 C; 2—0.5 C; 3—2.0 C; 4—5.0 C

4 CONCLUSIONS

In this study, a response surface method with central composite rotatable design (CCD) was used to investigate the effects of three important parameters including sintering temperature, sintering time and carbon content on the initial discharge capacity of LiFePO4/C prepared by carbothermal reduction technology. A statistical analysis (ANOVA) was carried out to evaluate the effects of process variables and their interaction towards the optimum conditions. The results show that sintering temperature and carbon content have a significant linear effect and quadratic effects on the initial discharge capacity, while the sintering time has a relatively smaller linear impact. The sintering time also shows a negative quadratic effect on the initial discharge capacity. However, interaction effects of sintering time with temperature or carbon content are both important. The model for optimization of experiment fits the experimental data well,with a multiple correlation coefficientR2of 0.9884.The optimum conditions obtained from the model is sintering temperature 652.0 °C, sintering time 8.48 h and carbon content 34.33 g·mol-1with a response of 150.8 mA·h·g-1. A confirmatory experiment carried out under the optimal conditions gave an initial discharge capacity of 147.2 mA·h·g-1, with a deviation of only 1.87%. The prepared LiFePO4/C showed a discharge capacity of 105.1 mA·h·g-1and the capacity retention ratio of 98.5% after 50 cycles at 5 C, exhibiting good rate performance.

1 Padhi, A.K., Nanjundaswamy, K.S., Goodenough, J.B., “Phospho-olivines as positive-electrode materials for rechargeable lithium batteries”,J.Electrochem.Soc., 144 (4), 1188-1194 (1997).

2 Padhi, A.K., Nanjundaswamy, K.S., Masquelier, C., Okada, S.,Goodenough, J.B., “Effect of structure on the redox Fe3+/Fe2+in iron phosphate”,J.Electrochem.Soc., 144 (10), 1609-1613 (1997).

3 Li, Z.H., Zhang, D.M., Yang, F.X., “Developments of lithium-ion batteries and challenges of LiFePO4as one promising cathode material”,J.Mater.Sci., 44 (10), 2435-2443 (2009).

4 Jugović, D., Uskoković, D., “A review of recent developments in the synthesis procedures of lithium iron phosphate powders”,J.Power Sources., 190 (2), 538-544 (2009).

5 Chen, Z.H., Dahn, J.R., “Reducing carbon in LiFePO4/C composite electrodes to maxing specific energy, volumetric energy, and tap density”,J.Electrochem.Soc., 149 (9), A1184-A1189 (2002).

6 Huang, Y., Park, K., Goodenough, J.B., “Improving lithium batteries by tethering carbon-coated LiFePO4to polypyrrole”,J.Electrochem.Soc., 153 (12), A2282-A2286 (2006).

7 Doeff, M.M., Wilcox, J.D., Kostecki, R., Lau, G., “Optimization of carbon coatings on LiFePO4”,J.Power Sources, 163 (1), 180-184(2006).

8 Kim, J.K., Cheruvally, G., Ahn, J.H., “Electrochemical properties of LiFePO4/C synthesized by mechanical activation using sucrose as carbon source”, J. Solid State Electrochem., 12 (7-8), 799-805(2008).

9 Bodoardo, S., Gerbaldi, C., Meligrana, G., Tuel, A., Enzo, S.,Penazzi, N., “Optimisation of some parameters for the preparation of nanostructured LiFePO4/C cathode”, Ionics, 15 (1), 19-26 (2009).

10 Chung, S.Y., Bloking, J.T.M., Chiang, Y., “Electronically conductive phospho-olivines as lithium storage electrodes”, Nat. Mater., 1 (2),123-128 (2002).

11 Wagemaker, M., Ellis, B.L., Hecht, D.L., Mulder, F.M., Nazar, L.F.,“Proof of supervalent doping in olivine LiFePO4”, Chem. Mater., 20(20), 6313-6315 (2008).

12 Bauer, E.M., Bellitto, C., Righini, G., Pasquali, M., “A versatile method of preparation of carbon-rich LiFePO4: A promising cathode material for Li-ion batteries”, J. Power Sources, 146 (1-2), 544-549(2005).

13 Xia, Y., Yoshio, M., Noguchi, H., “Improved electrochemical performance of LiFePO4by increasing its specific surface area”, Electrochimica Acta, 52 (1), 240-245 (2006).

14 Zhang, D., Cai, R., Zhou, Y.K., Shao, Z.P., Liao, X.Z., Ma, Z.F.,“Effect of milling method and time on the properties and electrochemical performance of LiFePO4/C composites prepared by ball milling and thermal treatment”, Electrochim. Acta, 55 (8),2653-2661 (2010).

15 Wang, K., Cai, R., Yuan, T., Yu, X., Ran, R., Shao, Z.P., “Process investigation, electrochemical characterization and optimization of LiFePO4/C composite from mechanical activation using sucrose as carbon source”, Electrochim. Acta, 54 (10), 2861-2868 (2009).

16 Barker, J., Saidi, M.Y., Swoyer, J.L., “Lithium iron (II) phosphoolivines prepared by a novel carbothermal reduction method”, Electrochem. Solid-State Lett., 6 (3), A53-A55 (2003).

17 Mi, C.H., Cao, G.S., Zhao, X.B., “Low-cost, one-step process for synthesis of carbon-coated LiFePO4cathode”, Mater. Lett., 59 (1),127-130 (2005).

18 Zhu, B.Q., Li., X.H., Wang, Z.X., Guo, H.J., “Novel synthesis of LiFePO4by aqueous precipitation and carbothermal reduction”, Mater. Chem. Phys., 98 (2-3), 373-376 (2006).

19 Wang, L.N., Zhang, Z.G., Zhang, K.L., “A simple, cheap soft synthesis routine for LiFePO4using iron(III) raw material”, J. Power Sources, 167 (1), 200-205 (2007).

20 Zheng, J.C., Li, X.H., Wang, Z.X., Guo, H.J., Zhou, S.Y., “LiFePO4with enhanced performance synthesized by a novel synthetic route”,J. Power Sources, 184 (2), 574-577 (2008).

21 Liu, H.P., Wang, Z.X., Li, X.H., Guo, H.J., Peng, W.J., Zhang, Y.H.,Hu, Q.Y., “Synthesis and electrochemical properties of olivine LiFePO4prepared by a carbothermal reduction method”, J. Power Sources, 184 (2), 469-472 (2008).

22 Chang, Z.R., Lv, H.J., Tang, H.W., Li, H.J., Yuan, X.Z., Wang, H.J.,“Synthesis and characterization of high-density LiFePO4/C composites as cathode materials for lithium-ion batteries”, Electrochim. Acta,54 (1), 4595-4599 (2009).

23 Liu, Z.L., Zhang, X.H., Hong, L., “Preparation and electrochemical properties of spherical LiFePO4and LiFe0.9Mg0.1PO4cathode materials for lithium rechargeable batteries”, J. Appl. Electrochem., 39(12), 2433-2438 (2009).

24 Liu, J., Wang, J.W., Yan, X.D., Zhang, X.F., Yang, G.L., Abraham, F.,Wang, R.S., “Long-term cyclability of LiFePO4/carbon composite cathode material for lithium-ion battery applications”, Electrochim.Acta, 54 (24), 5656-5659 (2009).

25 Wang, L., Liang, G.C., Ou, X.Q., Zh, X.K., Zhang, J.P., Cui, J.Y.,“Effect of synthesis temperature on the properties of LiFePO4/C composites prepared by carbothermal reduction”, J. Power Sources,189 (1), 423-428 (2009).

26 Aimable, A., Aymes, D., Bernard, F., Le Cras, F., “Characteristics of LiFePO4obtained through a one step continuous hydrothermal synthesis process working in supercritical water”, Solid State Ionics,180 (11-13), 861-866 (2009).

27 Liu, Y.Y., Cao, C.B., Li, J., “Enhanced electrochemical performance of carbon nanospheres-LiFePO4composite by PEG based sol-gel synthesis”, Electrochim. Acta, 55 (12), 3921-3926 (2010).

28 Arnold, G., Garche, J., Hemmer, R., Strobele, S., Vogler, C., Wohlfahrt-Mehrens, M., “Fine-particle lithium iron phosphate LiFePO4synthesized by a new low-cost aqueous precipitation technique”, J.Power Sources, 119-121 (1), 247-251 (2003).

29 Myers, R.H., Montgomery, D.C., Adweson-cook, C.M., Response Surface Methodology: Process and product optimization using designed experiments, John Wiley and Sons, Inc., New York, (2008).

30 Guven, G., Perendeci, A., Tanyolac, A., “Electrochemical treatment of deproteinated whey wastewater and optimization of treatment conditions with response surface methodology”, J. Hazard. Mater.,157 (1), 69-78 (2008).

31 Bashir, M.J.K., Aziz, H.A., Yusoff, M.S., Adlan, M.N., “Application of response surface methodology (RSM) for optimization of ammoniacal nitrogen removal from semi-aerobic landfill leachate using ion exchange resin”, Desalination, 254 (1-3),154-161 (2010).

32 Guo, J.Q., Luo, Y.E., Fan, D.D., Gao, P.F., Ma, X.X., Zhu, C.H.,“Analysis of metabolic products by response surface methodology for production of human-like collagen II”, Chin. J. Chem. Eng., 18(5), 830-836 (2010).

33 Zhang, C., Fan, D.D., Shang, L.A., Ma, X.X., Luo, Y.E., Xue, W.J.,Gao, P.F., “Optimization of fermentation process for human-like collagen production of recombinant Escherichia coli using response surface methodology”, Chin. J. Chem. Eng., 18 (1), 137-142 (2010).

34 Lola, K., Cai, S.H., Chen, K.C., “Optical resolution of DL-tartaric acid mediated by diastereomeric salts crystallization: A useful method for exploring and optimizing experimental conditions”, Chin.J. Chem. Eng., 10 (2), 244-248 (2010).

35 Joglekar, A.M., May, A.T., “Product excellence through design of experiments”, Cereal Foods World, 32 (12), 857-868 (1987).

36 Takahashi, M., Tobishima, S., Takei, K., Sakurai, Y., “Characterization of LiFePO4as the cathode material for rechargeable lithium batteries”, J. Power Sources, 97/98 (1), 508-511 (2001).

37 Yamada, A., Chung, S.C., Hinokuma, K., “Optimized LiFePO4for lithium battery cathodes”, J. Electrochem. Soc., 148 (2), A224-A229(2001).

38 Huang, H., Yin, S.C., Nazar, L. F., “Approaching theoretical capacity of LiFePO4at room temperature at high rates”, Electrochem.Solid-state Lett., 10 (4), A170-A172 (2001).

39 Andersson, A.S., Thomas, J.O., “The source of first-cycle capacity loss in LiFePO4”, J. Power Sources, 97/98 (1), 498-502 (2001).

40 Prosini, P.P., Carewska, M., Scaccia, S., Wisniewski, P., Passweini,S., Pasquali, M., “A new synthetic route for preparing LiFePO4with enhanced electrochemical performance”, J. Electrochem. Soc., 149(7), 886-890 (2002).