基于Hilbert变换的复合材料声学性能检测方法研究❋

樊程广,潘孟春,罗飞路,罗诗途,谭项林

(国防科学技术大学机电工程与自动化学院,湖南长沙 410073）

0 引 言

纤维增强树脂基复合材料是应用最为广泛的复合材料,具有一系列的优良性能,因此在航空工业领域得到了广泛的应用,尤其是在飞机的制造上,典型应用如直升机桨叶[1-2].在纤维增强树脂基复合材料广泛应用的同时,人们对其性能的无损检测和评估也在同步进行.声学性能是评价材料的重要指标,从不同的角度来看,材料的机械性能和显微结构等都能够利用声学性能来表征,因此准确测量材料声学性能是一个关键的问题[3].在复合材料的无损检测技术中,超声检测具有灵敏度高、穿透能力强、检测速度快等优点,因此发展最快、应用最广泛[4-6].

19世纪末20世纪初,德国著名数学家David Hilbert提出了Hilbert变换方法,目前,该方法已经广泛应用于各工程领域.例如,Hilbert变换用于故障诊断[7]、信号解调[8]、时频分析[9]、电压闪变测量[10]等.Hilbert变换方法既能克服傅里叶变换方法分辨率低的缺点,又能同时克服在小波变换方法中需要选择小波基的困难和小波变换后信号能量泄露的缺点,因此,将Hilbert变换引入复合材料声学性能的测量是一个有意义的研究方向[11].

本文首先详细介绍了Hilbert变换原理和声学性能测量原理,然后利用Hilbert变换对实测的超声回波信号进行分析,进而求得材料相关声学性能参数,并对不同种类的复合材料进行对比评估.

1 原 理

1.1 Hilbert变换

1.1.1 超声回波信号的数学模型

超声波入射至被测材料,当超声波遇到非连续性结构或边界返回时,产生振荡波,即为超声回波信号f(t),超声回波信号具有窄带信号的特征[12]

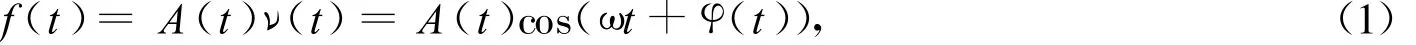
式中:A(t)为超声回波信号的幅值函数;ω为超声换能器的固有激发频率;φ(t)为相位函数.

从信号分析的角度来看,超声回波信号是对高频载波信号的低频调制,其中,高频信号ν(t)为载波信号,缓慢变化的幅值函数 A(t)为调幅信号,也就是超声回波信号的包络,体现了信号的整体起伏特性,包含了被测材料的关键信息.

1.1.2 超声回波信号的Hilbert分析

超声回波信号 f(t)是实信号,实信号的傅里叶变换包含负的频率成分,不利于信号分析,因此引入解析信号的概念.Hilbert变换就是一种将时域实信号变换为时域解析信号的数学处理过程[13].超声回波信号 f(r)的Hilbert变换 fh(t)定义

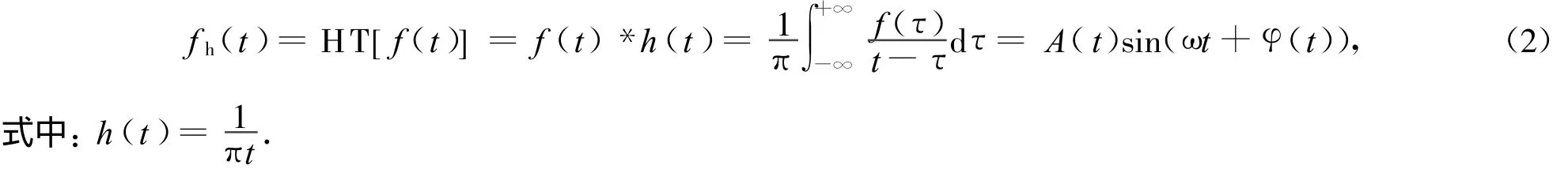
基于超声回波信号 f(t)的解析函数fa(t)

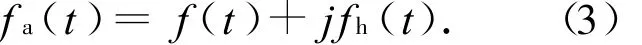
式(3)表明:解析函数 fa(t)的实部是超声回波信号 f(t),虚部是超声回波信号 f(t)的Hilbert变换 fh(t).

定义 f(ω)为 f(t)的傅里叶变换,fh(ω)为 fh(t)的傅里叶变换,fa(ω)为fa(t)的傅里叶变换,根据Hilbert变换的性质可以得到

式中:sgn(ω)为符号函数.

因此,在已有超声回波信号 f(t)的前提下可由 f(ω)得到 fa(ω),进而求得解析函数 fa(t).

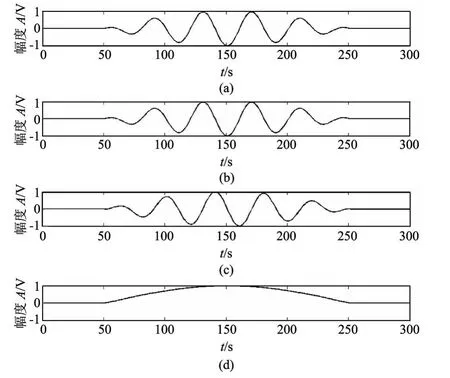
图1 模拟超声回波信号及其Hilbert分析Fig.1 Simulation of the ultrasonic echo signalw ith its hilbert transform

根据以上分析,解析函数 fa(t)又可表示成

由式(1)和式(6)可知:解析函数 fa(t)和超声回波信号 f(t)的振幅函数相同,同为 A(t),相位函数相同,同为 ωt+φ(t).因此超声回波信号 f(t)的瞬时包络为

1.1.3 仿真分析

图1表示了一个模拟超声回波信号的Hilbert分析过程,图1(a)～(d)分别代表模拟的超声回波信号、基于超声回波信号的解析信号的实部、基于超声回波信号的解析信号的虚部、超声回波信号的包络,从图1中可以看出:经过Hilbert变换后的超声回波信号包络与实际超声回波信号的包络一致.

1.2 声学性能测量原理

声速、声阻抗以及衰减系数是描绘超声波在被测材料中传播时的声学参数,是表征材料成分和组织结构的重要参数,材料的弹性模量、材料的显微结构、形态以及相应的机械性能都能用声学参数来表征.例如通过测量声速可以确定材料的弹性模量,根据声速和衰减系数可以表征材料的显微结构[14].

1.2.1 声 速

采用超声脉冲回波法,根据被测材料厚度d和超声波在材料中传播时的回波时间间隔t,即可准确测量超声波在被测材料中的传播速度

1.2.2 声阻抗

声阻抗z的计算

式中:ρ为被测材料密度;v为声速.

1.2.3 衰减系数

超声波的衰减主要包括:被测材料对超声波的衰减、耦合剂对超声波的衰减以及超声波扩散引起的衰减[15-16].超声波探头通过耦合剂和被测材料直接耦合在一起,属于近场区域测量,因此超声波的扩散损失忽略.耦合剂的使用对超声波的传播产生一定的能量损失,在计算时应考虑在内.因此,衰减系数

式中:A1为被测材料一次反射回波的幅值;A2为被测材料二次反射回波的幅值;α(z c,z o)为耦合剂对超声波的衰减系数;z o为耦合剂的声阻抗;z c为被测材料的声阻抗;d为被测材料厚度.

2 检测系统

检测系统原理框图如图2所示.检测系统采用超声脉冲回波法,超声波探伤仪通过激发探头激发超声波,超声波经耦合剂的耦合作用到达被测试件的前表面,一部分由前表面反射回接收探头,另一部分入射试件内部,由后表面反射回接收探头.接收探头将接收到的反射回波信号通过数据采集卡进行高速采样,并将采样数据传入计算机进行存储和处理,处理结果可在显示器上实时显示.

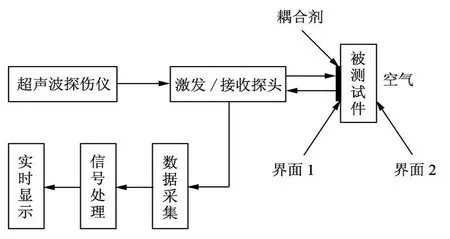
图2 检测系统原理框图F ig.2 The schematic diagram of inspection system

图2中,界面1为耦合剂/被测试件界面,耦合剂选用机油,机油具有良好的耦合性能,保证了被测试件的前表面具有良好的耦合状况;界面2为被测试件/空气界面,由于空气对超声波有强烈的衰减作用,因此保证了后表面反射回波信号有足够的强度返回到接收探头.

3 实验结果及分析

检测系统中的超声波探伤仪选用常州新区大平超声波仪器有限公司生产的CUT-2007型超声波探伤仪,选用超声纵波探头激发和接收超声波,探头工作频率为2.5 MHz,超声波垂直于被测试件表面入射.被测试件1选用编织玻璃纤维环氧树脂基复合材料层压板,尺寸大小为220mm×215 mm×7 mm;被测试件2选用单向碳纤维环氧树脂基复合材料层压板,尺寸大小为300mm×300mm×3mm.

图3(a)和图3(b)分别为被测试件1和被测试件2的实物图.

图3 被测试件实物图Fig.3 Thesubstan ce d iagram of specim en

图4和图5分别表示被测试件1和被测试件2中实测超声回波信号的Hilbert变换分析过程.图4(a)和图5(a)为实测超声回波信号,图4(b)和图5(b)为去除噪声后的超声回波信号,图4(c)和图5(c)为Hilbert变换后的超声回波包络信号,图4(d)和图5(d)为归一化的超声回波包络信号.图中,S代表激发的超声信号,R1代表一次反射回波信号,R2代表二次反射回波信号.

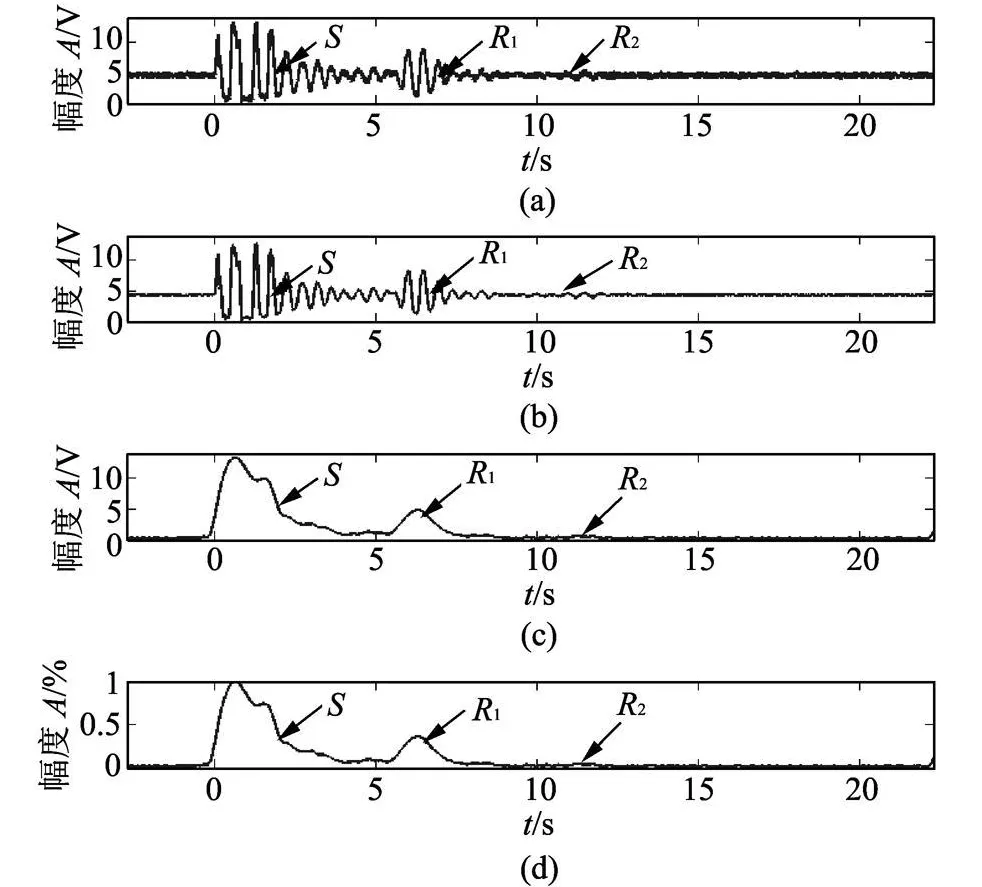
图4 被测试件 1实测超声回波信号及其Hilbert分析Fig.4 The measured ultrasonic echo signal w ith its hilber t transform of specimen 1

图5 被测试件2实测超声回波信号及其 Hilbert分析Fig.5 Them easured ultrason ic echo signal w ith its hilbert transform of specim en 2

由图4和图5可知:Hilbert变换方法能够以较小的误差跟踪实测超声回波信号的包络,在准确跟踪包络信号的基础上可进一步计算被测试件的声学性能参数.

经过对被测试件1和被测试件2不同位置的多次测量,得到被测试件1的声学性能参数,如表1所示,被测试件2的声学性能参数如表2所示.

对表1和表2的实验数据分析可知:基于Hilbert变换的超声检测方法能够准确测量复合材料的声学性能,误差控制在2.5%以内.此外,超声波在选用的两种复合材料中的传播速度相近,但声阻抗和衰减系数不同,这是由于在不考虑超声扩散损失和使用相同耦合剂的情况下,被测试件本身的性能和组织结构对超声波的衰减起主要作用,试件1使用玻璃纤维和环氧树脂,纤维编织排列,试件 2使用碳纤维和环氧树脂,纤维单向排列,不同的纤维种类、纤维体积含量以及纤维排列方式造成了声阻抗和衰减系数的差异.

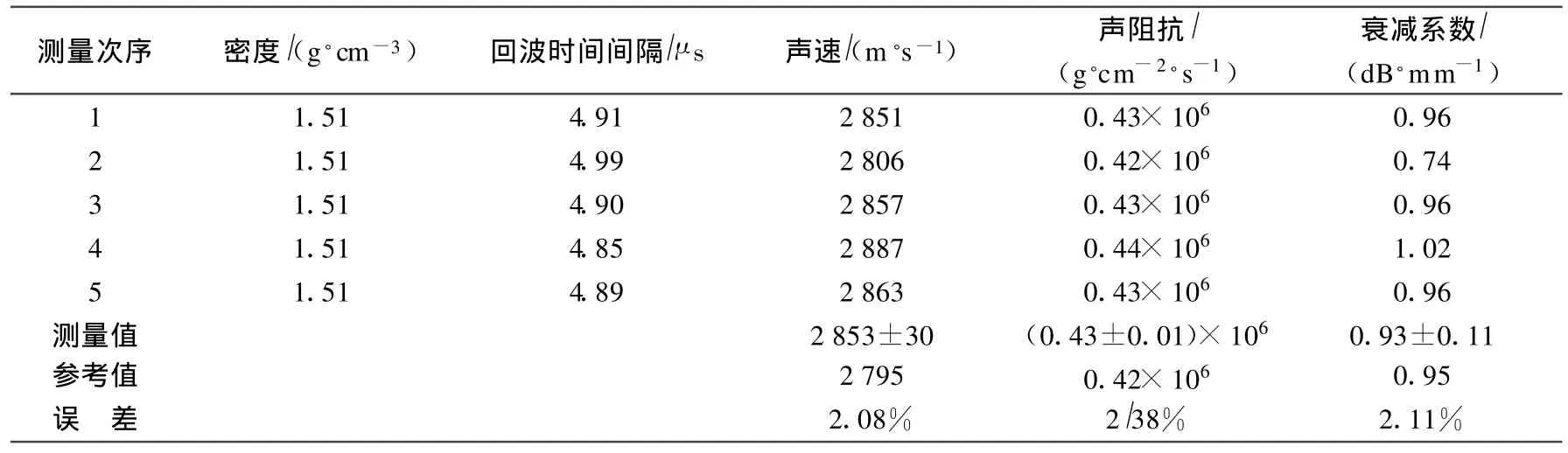
表1 被测试件1声学性能参数(试件厚度7 mm)Tab.1 Acoustic property of specimen 1(specimen thickness:7 mm)

表2 被测试件 2声学性能参数(试件厚度3 mm)Tab.2 Acoustic property of specimen 2(specimen thickness:3 mm)

4 结 论

1)从原理上介绍了Hilbert变换和复合材料声学性能的测量,将Hilbert变换引入复合材料声学性能的测量;

2)采用超声脉冲回波法对两种不同类型的复合材料层压板进行检测,利用Hilbert变换对检测到的超声回波信号进行分析和处理;

3)结果表明:本方法能够准确测量复合材料声学性能,测量误差小于2.5%,同时,能够有效评估复合材料本身性能.

[1] Birt EA,Smith R A.A review of NDEmethods for porositymeasurement in fibre-reinforced polymercomposites[J].Non-Destructive Testing and Condition Monitoring,2004,46(11):681-686.

[2] 吴瑞明,周晓军,王邦凯.复合材料超声C扫描多传感器信息融合技术[J].传感技术学报,2005,18(3):561-564.

Wu Ruim ing,Zhou Xiaojun,Wang Bangkai.Study onmultisensor information fusion in ultrasonic C scan system of com pos-itematerial[J].Chinese Journal of Sensors and A ctuators,2005,18(3):561-564.(in Chinese)

[3] 段剑,王从科,于波,等.纤维增强复合材料声学性能检测方法研究[J].测试技术学报,2004,18(1):39-42.

Duan Jian,Wang Congke,Yu Bo,et al.Research on testmethods of acoustics performance about resin-based composites[J].Journalof Testand Measurement Technology,2004,18(1):39-42.(in Chinese)

[4] 邢娅浪,徐章遂,陈鹏,等.超声波技术在现代战机复合材料结构损伤缺陷检测中的应用[J].测试技术学报,2004,18(3):221-224.

Xing Yalang,Xu Zhangsui,Chen Peng,etal.App lication of ultrasonic detection in detecting flaw in compositematerial of modern battleplan[J].Journalof Test and Measurement Technology,2004,18(3):221-224.(in Chinese)

[5] Reyno ldsW N.Nondestructive testing of fibre-reinforced compositematerials[J].Materials&Design,1985,5(6):256-270.

[6] Bayraktar E,Antolovich SD,Bathias C.New developments in non-destructive controls of the compositematerials and applications in manufacturing engineering[J].Journal of Materials Processing Technology,2008,206:30-44.

[7] 李智,陈祥初,刘政波.包络分析及其在设备故障诊断中的应用[J].测试技术学报,2002,16(2):92-95.

Li Zhi,Chen Xiangchu,Liu Zhengbo.Envelopment analysis and its application in the fau lt diagnosis[J].Journal of Test and Measurement Technology,2002,16(2):92-95.(in Chinese)

[8] 丁康,胡晓斌,谢明.解调分析的一种优化方法[J].振动工程学报,1998,11(2):235-240.

Ding Kang,Hu Xiaobin,XieMing.An optim izedmethod of demodulation[J].Journal of Vibration Engineering,1998,11(2):235-240.(in Chinese)

[9] Soum ik Sarkar,KushalMukherjee,Asok Ray.Generalization of H ilbert transform for symbolic analysisof noisy signals[J].Signal Processing,2009,89:1245-1251.

[10] 舒泓,王毅.基于数学形态滤波和Hilbert变化的电压闪变测量[J].中国电机工程学报,2008,28(1):111-114.

Shu Hong,W ang Yi.Voltage flicker detectionmethod based onmathematicalmorphology filterand Hilbert transform[J].Proceedings of the CSEE,2008,28(1):111-114.(in Chinese)

[11] 吴斌,邓菲,何存富.超声导波无损检测中的信号处理研究进展[J].北京工业大学学报,2007,33(4):342-348.

W u Bin,Deng Fei,He Cunfu.Review of signalp rocessing in ultrasonic guided w avesnondestructive testing[J].Journal of Beijing University of Technology,2007,33(4):342-348.(in Chinese)

[12] 李珑.超声无损检测和无损评价的一种新方法研究[J].声学学报,1993,18(6):409-414.

Li Long.A new method for u ltrasonic NDT and NDE[J].Acta A custica,1993,18(6):409-414.(in Chinese)

[13] IvanW Selesnick.Hilbert Transform Pairs of W avelet Bases[J].Signal Processing Letters,2001,8(6):170-173.

[14] Graciet C,Hosten B.Simultaneousmeasurement of speed,attenuation,thickness and density with reflected ultrasonic waves in plates[C].Ultrasonic Symposium,1994,2:1219-1222.

[15] 王浩全,韩炎,曾光宇.非金属复合材料超声波衰减系数测定研究[J].测试技术学报,2002,16(4):249-251.

W ang Haoquan,Han Yan,ZengGuangyu.The research onmeasuring theu ltrasonic attenuation coefficientaboutnonmetal compositematerials[J].Journalof Test and Measurement Technology,2002,16(4):249-251.(in Chinese)

[16] Biwa S,Idekoba S,Ohno N.Wave attenuation in particu late polymer com posites[J].Mechanicso fMaterials,2002,34:671-682.