基于灰色理论的事故伤亡预测分析*

李俊勤，贾智伟

(1.河南理工大学安全科学与工程学院，河南焦作454003;2.河南省煤矿瓦斯与火灾防治重点实验室，河南焦作454003)

1982年邓聚龙教授首次提出并创立了灰色系统理论。运用灰色系统理论预测分析可以将一组规律性不强或毫无规律可循、杂乱无章的原始数据序列通过一系列数据生成方法(遗传因子累加法、直接累加法、自适性累加法、加权累加法、移动平均法等)，变得有章可循，具有明显的规律性，从而使数学界一直认为不能解决的微积分方程建模问题得以解决。

人-机-环境系统是导致事故发生的根本元素，依据灰色系统预测理论，该系统是一个部分信息不明确与部分信息明确共存的灰色系统，因此运用GM(1，1)灰色预测模型对企业伤亡事故进行预测分析是可行的，这样可避免由于事故的偶然性、不确定性和突发性以及事故历史数据缺失或不准确造成的预测精度低的问题。

本文以河南省平顶山市某化工企业为例，运用GM(1，1)灰色预测模型，对该企业千人负伤率的变化趋势进行了建模，并在此基础上进行了预测研究。

1 灰色预测模型

1.1 灰色预测原理

灰色系统预测原理是把离散的、随机的原始数据进行n次累加生成，得到规律性较强的序列，然后在此基础上建模，最后进行n次累减还原到预测值。

1.2 GM(1，1)模型的建立

GM(1，1)模型是一阶的一个变量的微分方程模型。模型建立步骤如下[1]：

(1)数据的累加生成

设原始离散数据序列

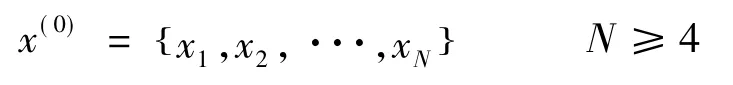
式中N为序列长度，对其进行一次累加生成处理。

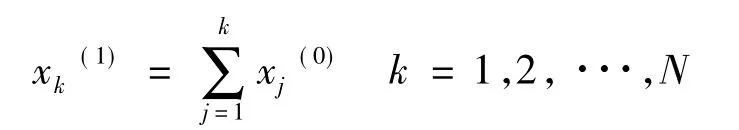
(2)方程的白化

(3)方程系数的求解

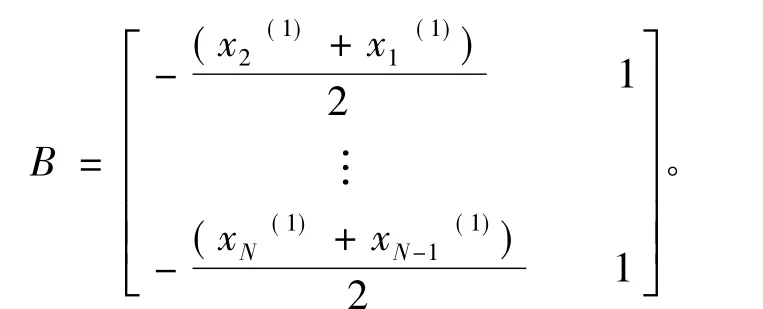
可由下式求得最小二乘解：

(4)求解方程

根据式(2)可得到下面的预测公式。

时间响应方程[即式(1)的解]为：

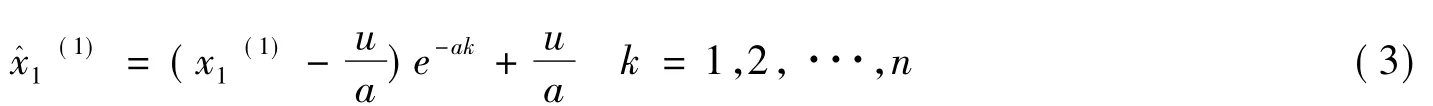
离散响应方程为：

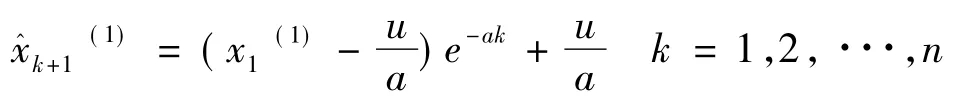
(5)预测序列的还原

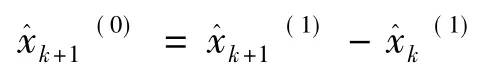
在GM(1，1)模型的拟合残差中通常还有一部分动态信息是有效的，因此可以通过建立残差GM(1，1)模型对原模型进行修正。

1.3 预测模型的后验差检验

可以通过后验差及关联度对预测模型进行检验，用后验差进行检验的方法如下：记0阶残差为：

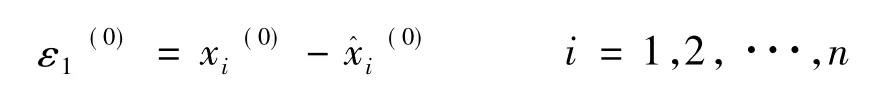
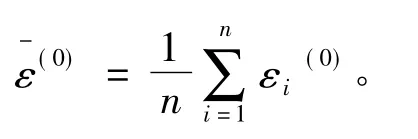
残差方差为：

随着我国各个领域企业的不断发展，商业经济领域的发展规模也在不断扩大，在各式各样的企业中，财务管理所涉及的管理工作已经不再局限于企业各个阶段的数据分析以及整理反馈，传统的管理模式已经不能使企业发展得到满意的效果。就当今企业而言，企业运作的核心与资金链的把控都与财务管理息息相关，企业的财务部门可以为企业的发展提供资金方案，确保企业的正常运作，从而使企业的发展可以更加稳定，因此，企业的财务管理在决策和管理上是非常重要的，因此，在财务管理上要科学合理的进行管制。在经济快增长的新中国，财务管理在管理模式上要适当加以改进。

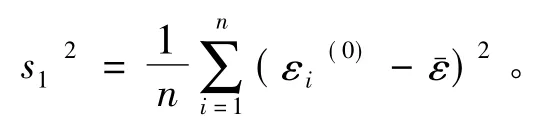
原始数据均值为：

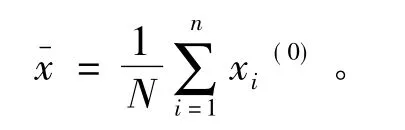
原始数据方差为：

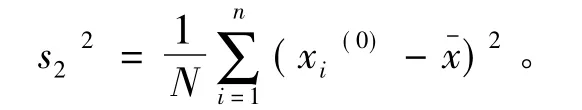
因此可计算后验差检验指标。

后验差比值为：

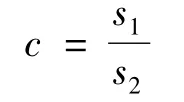
小误差概率为：

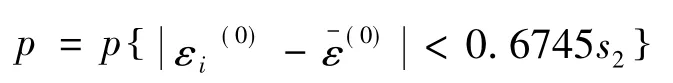
精度检验等级可以按照上述两个指标，从表1查出[3]。

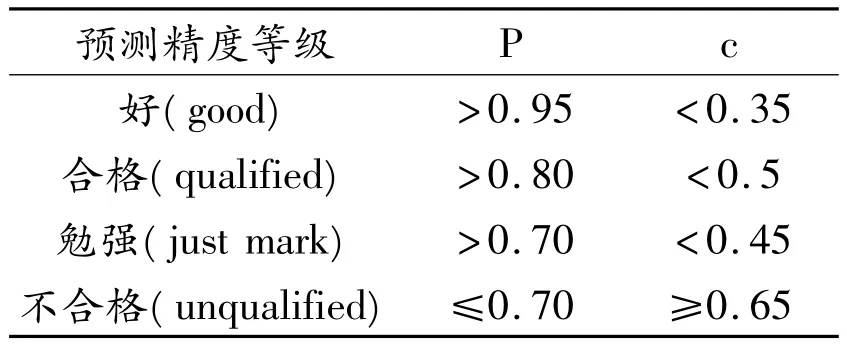
表1 精度检验等级

表2 某化工企业2007～2010年千人负伤率

2 灰色预测实例分析

已知某化工企业2007～2010年千人负伤率(如表2所示)，利用GM(1，1)模型对该企业2011年、2012年的千人负伤率进行灰色预测，并对拟合精度进行后验差检验。

故可建立数据矩阵B，yN：

由式(2)可得：

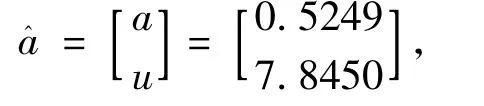
则a、u代入式(3)可得到：

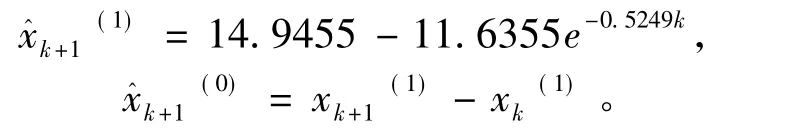
计算结果如表3所示。进行后验差检验：

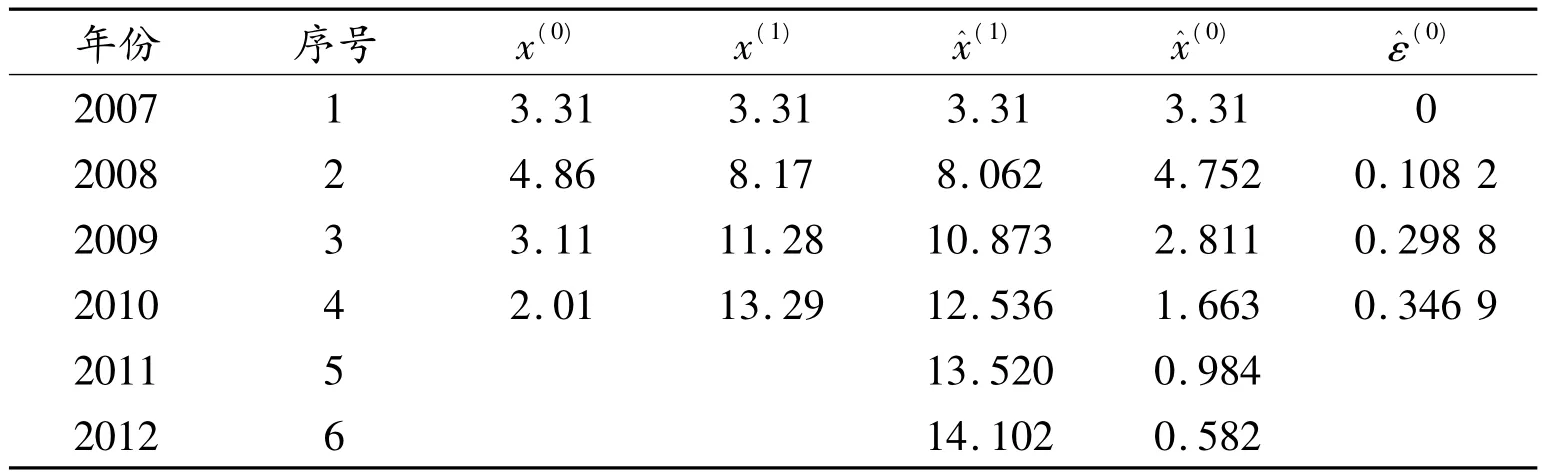
表3 计算结果

对照表1可知，灰色系统预测拟合精度为好，预测结果正确可靠。

3 结论和建议

(1)在预测样本不够大、历史数据不足的情况下，运用灰色理论进行预测分析，不仅有效地避免了预测精度不高的现象，而且得出的预测数据能很好地反映出企业未来安全状况的现实规律，这对企业的安全生产具有一定的指导意义。

(2)企业的事故伤亡率是动态的，在对安全生产采取有力的措施后，会有所降低，但事故伤亡率无限制地递减至0是不可能的，在达到某一定数值后，递减变化将会变得非常缓慢乃至停滞，甚至也有可能出现回升。因此，每隔一段时间更新信息，重新建模是非常必要的。

(3)尽管预测过程是可信的，但影响化工企业安全生产的因素很多，为达到预测目标，企业应加强日常安全管理，认真落实各级人员安全生产责任制，及时消除事故隐患，认真做好安全教育，杜绝“三违”，且不可产生麻痹思想。

[1] 邓聚龙.灰色系统理论基本教程[M].武汉：华中理工大学出版社，1990.

[2] 景国勋.灰色预测理论在煤矿上的应用[J].地质勘探安全，1994(2)：23-25.

[3] 赵耀江.灰色预测在安全生产中的应用[J].太原工业大学学报.1997，28，(4)：93-96.

[4] 舒金兵.灰色预测在矿山企业伤亡事故预测中的应用[J].工业安全与环保，2008，34，(11)：61-62.