基于跳扩散过程的欧式双向期权定价*
2012-02-08胡素敏张晓果
胡素敏,张晓果
(河南城建学院数理系,河南平顶山467036)
期权定价问题一直是金融数学和金融工程学研究的核心问题之一.在以往的期权定价中,人们普遍假设标的资产价格服从几何布朗运动,它是一个连续的随机过程,而在金融市场上,一些重要信息的出现会刺激股票价格发生不连续的跳跃,因此股票价格应包含连续扩散过程和不连续的跳跃过程两方面.关于股价服从跳扩散过程的期权定价方面,周圣武[1]研究了股价服从跳扩散过程的标准欧式期权定价,刘宣会[2]研究了基于跳扩散过程的一类亚式期权定价.K.Zhang[3]和M.Freeman[4]等研究了跳扩散模型下期权的定价和应用问题.
本文将用跳扩散过程研究股价的演化行为,即用Poisson过程描述股价的跳跃行为,用几何Brown运动刻画股价的连续波动行为,在此基础上应用风险中性原理研究跳扩散过程的欧式双向期权,推导了标的资产价格服从跳扩散过程的欧式双向期权定价公式.
1 股票价格的跳扩散行为
研究跳扩散过程下欧式双向期权的定价问题,需要如下假设:股票价格ST遵循Ito过程[5]
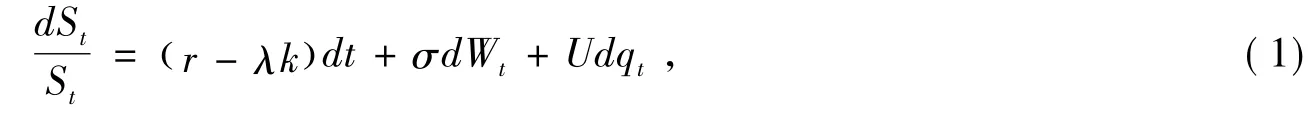
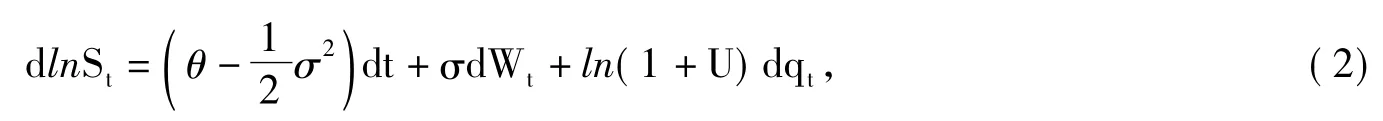
求解式(2),并应用Poisson过程的性质qT-qt=qτ(τ=τ-t),可得T时刻股票价格ST的概率分布
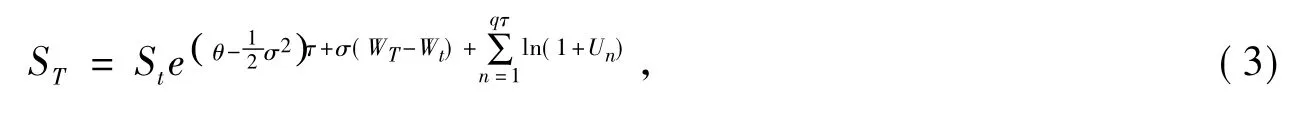
其中:τ=T-t;Un表示股票价格在第n个跳跃时刻tn的跳跃幅度,并假设U1,U2,…,Un,…是一系列独立分布的随机变量.应用全期望公式可得股票价格在T时刻的数学期望.为表述方便,本文将沿用Merton[7]的假设:
假设U、qt、Wt相互独立,且1+U服从对数正态分布,即

其中μ、σU为常数.
于是当qτ=n时,由正态分布的可加性可得:
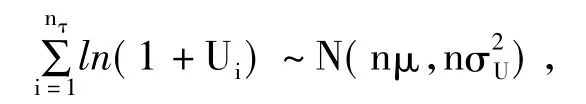
从而存在标准正态随机变量Z2~N(0,1),使得随机和可表示为:

而且由于U、qt、Wt相互独立,可知Z1、Z2也相互独立.
由式(3)和式(5)以及正态分布的可加性可知,当qτ=n时,存在标准正态随机变量Zn~N(0,1),使得
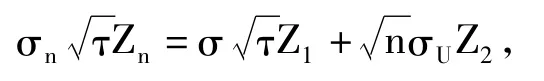

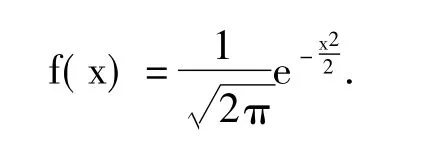
3 无红利支付的欧式双向期权定价
欧式双向期权是指期权持有者可以在未来某T时刻以规定的价格K买进或卖出某指定标的资产,且标的资产价格满足式(1),由于在T时刻欧式双向期权的权益为:
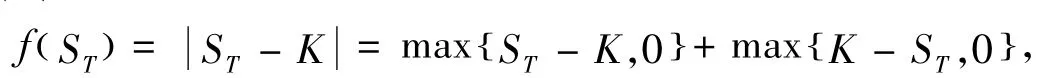
即欧式双向期权的终端收益可以分解为具有相同到期时刻和相同执行价格的同一种标的资产的一个买入期权的终端收益和一个卖出期权的终端收益之和.
本文在推导欧式双向期权定价的过程中,需要用到下列基本假设[6-7]:(1)标的股票价格服从跳扩散过程,且满足式(1);(2)无风险利率r是常数;(3)标的股票价格的波动率σ是常数;(4)不存在交易费用;(5)在期权的有效期内标的股票无红利支付;(6)不存在无风险套利机会.
根据风险中性定价原理,在风险中性概率测度Q下,标准欧式股票看涨期权在当前t(t<T)时刻的价值为:
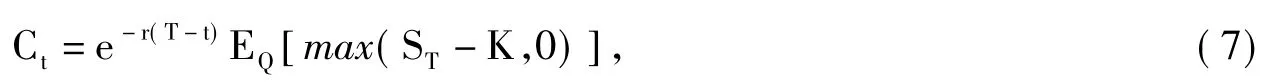
其中EQ表示在风险中性概率测度Q下的数学期望.
引理1[1]标的股票价格St服从式(1)、执行价格为K的标准欧式看涨期权在t时刻的价值为:
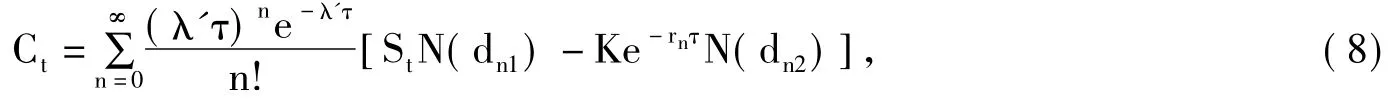
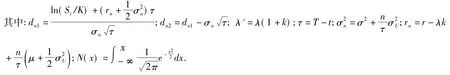
引理2[1]标的股票价格St服从式(1)、执行价格为K的标准欧式看跌期权在t时刻的价值为
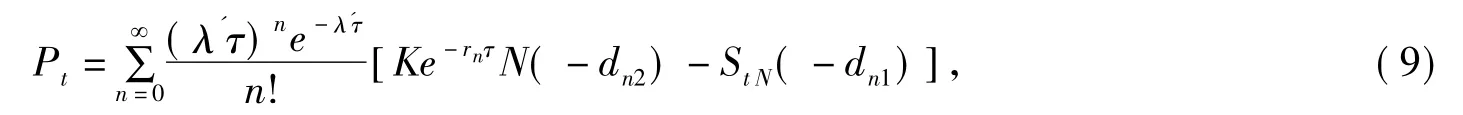
式中符号同引理1,证明过程与引理1类似.
定理1[1]标的股票价格St服从式(1)、执行价格为K的欧式双向期权在t时刻的价值为:
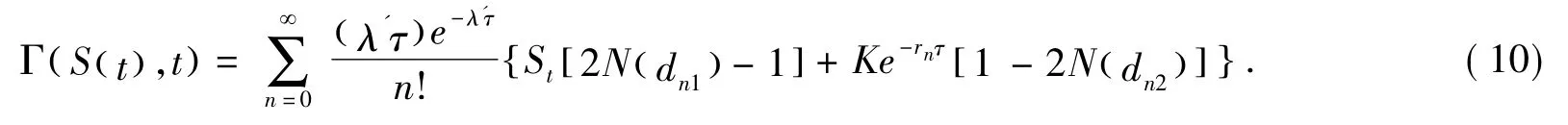
证明
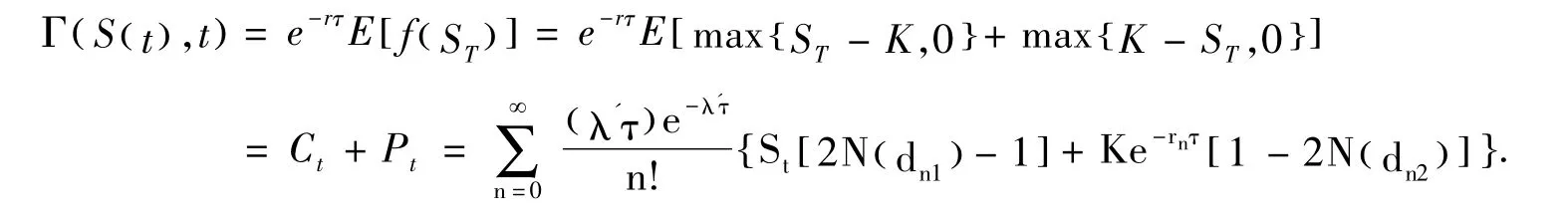
推论1当n=0时,即股票价格不发生跳跃时,得欧式双向期权的价值为此定价公式与董跃武[8]得到的定价公式完全相同.
[1] 周圣武.基于跳扩散过程的欧式股票期权定价与风险度量研究[D].徐州:中国矿业大学,2009.
[2] 刘宣会.基于跳扩散过程的一类亚式期权定价[J].系统工程学报,2008,23(2):142-147.
[3] Leland H E.Option pricing and replication with transaction costs[J].Journal of Finance,1985(40):1283-1301.
[4] Markowitz H M.Portfolio selection[J].Journal of Finance,1952(1):77-91.
[5] 黄志远.随机分析学基础[M].北京:科学出版社,2001.
[6] Merton R C.Option pricing when underlying stock returns are discontinuous[J].Journal of Financial Economics,1976(3):125-144.
[7] Black F,Scholes M.The pricing of options and corporate liabilities[J].Journal of Political Economy,1973(81):637-659.
[8] 董跃武.欧式双向期权的定价问题[J].上海铁道大学学报,1999,20(6):71-73.
