具有对数奇性耦合的半线性抛物方程组的全局解与猝灭

孙仁斌，袁海峰

(中南民族大学数学与统计学学院，武汉430074)

本文考虑如下抛物方程组的初边值问题:

其中Ω是N维空间中具有光滑边界∂Ω的有界区域，常数 α，β＞0，0＜b＜1．

对于问题(1)，由于方程中对数项具有奇异性，如果在某一时刻，解函数u或者v的值趋近于b，问题就会发生所谓的猝灭现象，其定义如下:

如果存在有限时刻T，使得:

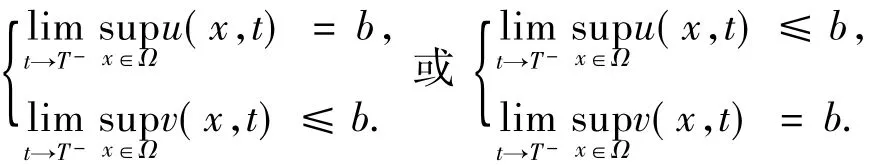
成立，就称问题(1)的解在时刻T猝灭．

关于单个抛物方程的初边值问题:

其中f(s)具有奇性:对于猝灭现象的研究始于文献［1］，文献［2］给出了问题存在整体解的条件，在文［3-5］中，针对Ω为一维区间及n维球形区域的情形进行讨论，在文献［6，7］中，对Ω为任意的n维区域的情形进行讨论．一些早期的结果的基本结论是:当区域Ω充分小时，解的存在是整体的，当Ω充分大时，解会在有限时刻发生猝灭现象．更进一步，关于猝灭时间的估计，猝灭点集的数量以及猝灭速率的估计和解在猝灭时刻的渐近分析等，大多都是针对f(s)=(1－s)－α的情形，展开深入的分析，已经取得了相当丰富的结果．在文献［8］中，当问题(2)中的f(s)=－ln(αs)，Ω是一维区间的情形时，进行了讨论．在文献［9］中，对f(s)=－αln(b－u)且Ω⊂RN时的情形进行了讨论，得到了解在有限时刻发生猝灭的条件，并对猝灭速率进行了估计．

对于抛物方程组的猝灭现象的研究，近年来也有了一些结果［10-12］，大多也是针对方程组右边的奇性函数为f(u，v)=(1－v)－α，g(u，v)=(1－u)－β的情形进行讨论．

本文讨论的问题(1)中方程组右边的奇性函数为对数函数，与幂函数比较，其引发猝灭的能力要更弱一些，因此讨论起来难度会更大一些．我们将文献［9］中关于单个方程的结果经过适当的处理，推广到方程组的情形，得到了解全局存在和在有限时刻猝灭的条件．

1 全局解的存在性

为了得到问题(1)的全局解，我们要设法找到它的一个全局存在的上解．为此考察与之对应的带有奇性的椭圆方程组的边值问题:

在区域Ω的外部取定一个点x0=(x01，x02，…，x0N)，令k是一个待定的正数，γ=max(α，β)，构造函数:

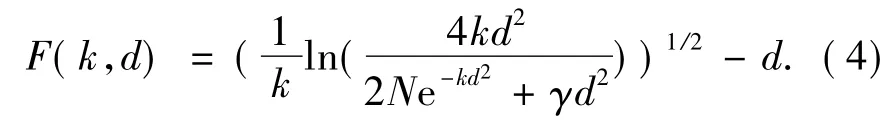
引理1由(4)式定义的函数F(k，d)一定有正的最大值D*．

证明要使F(k，d)＞0，只需，或(4k－γekd2)d2＞2N，所以，只要取k，d，使:

就有F(k，d)＞0，而当k，d充分大时，F(k，d) 显然是有界的，因此引理的结论成立．

下面我们构造问题(3)的上解．令:

经过计算有:

设D为Ω的直径，则x∈Ω时有d2≤|x－x0|2≤(d+D)2，为使(7)式成立，只需:

而γ=max(α，β)，因此当D≤F(k，d)时，上述不等式成立．

在边界x∈ ∂Ω 上，要使 ¯u≥ 0，¯v≥ 0，只需:

现在假设当k，b在满足不等式(8)的条件下，函数F(k，d)在k=k0，d=d0点取到正的最大值D*，再取一点x0∉Ω，使dist(x0，Ω)=d0，由此按照(6)式构造的函数就是问题(3)的一个上解，即得到定理1．

定理1存在正数D*，使得当区域Ω的直径D不超过D*时，问题(3)存在上解．

关于D的取值范围，我们可以作一些分析．

由于F(k，d) ≥D≥0，故或:

选取k使4k－γekd2最大，即，此时，不等式(9)式化为:

不等式(8)化为:

由此可以得到抛物方程组的初边值问题(1)的全局解的存在性．

定理2在定理1的条件下，问题(1)存在全局解．

证明设U(x)，V(x)是问题(3)的一个正解，则容易验证是问题(1)的一个上解是问题(1)的一个下解，则问题(1)在上解与下解之间存在唯一解［13］．而上解与下解都是全局存在的，因此问题(1)存在全局解．

2 解的有限猝灭

设λ1与φ(x)是如下特征值问题的第一特征值与相应的特征函数:

则 λ1＞0，且当x∈Ω时，φ(x)＞0，我们假设利用问题(1) 中的方程，我们有:

由Jensen不等式，有:

类似地有:

记 δ=min(α，β)．两式相加得:

令g(s)=－λ1s－δln(2b2－bs)，0＜s＜2b，则当λ1时，g(s)＞0， 记有，记则h1(0)=2b2ln(2b2)＜0，0，且0，因此函数h'(s)在(0，2b)内有唯一的零点s0，易知h(s0)是h(s)在(0，2b)内惟一的最小点，设相应的最小值为:

我们知道，特征值λ1与区域Ω有关，Ω越大，λ1越小，由此我们可得到这一部分的主要结果．

定理3设m为由(13)式给出的正常数，2b2＜1，区域Ω适当大，使λ1＜m，则问题(1)的解在有限时刻发生猝灭，且猝灭时刻T满足T1≤T≤T2，其中:

证明设问题(1)的解的最大存在区间为［0，．当 0＜t＜T时因此w(t)＜2b，由(12)式及λ1＜m有w'(t)＞0，于是两边积分得:

令t→T，有w(t)≤2b，因此T≤T2成立．由于T2＜+∞，故有T＜+∞，即问题(1)的解会在有限时刻发生猝灭．

为了得到猝灭时刻T的下限，考虑初值问题:

易知解W(t)的最大存在区间是［0，T1］，t＜T1时，W(t)＜b．令，则是问题(1) 的一个上解［13］，故有u(x，t)≤W(t)，v(x，t) ≤W(t)，于是sup(u(x，t)，v(x，t))≤W(t)，如果T＜T1，令t→T－，得W(T) ≥b，产生矛盾，从而T≥T1成立，证毕．

［1］ Kawarada H．On solutions of initial-boundary value problem forut=uxx+1/(1 －u)［J］．Publ Res Inst Math Sci，1975，10:729-736．

［2］ Acker A，WalterW．On the global existence of solutions of parabolic differential equation with a singular nonlinear term［J］．Nonlinear Analysis，1978，2:499-505．

［3］ Chan CY，Kwong M K．Quenching phenomena for singular nonlinear parabolic equations［J］．Nonlinear Analysis，1988，12:1377-1383．

［4］ Acker A，Kawohl B．Remarks on quenching［J］．Nonlinear Analysis，1989，13:53-61．

［5］ Guo J S．On the quenching behavior of the solution of a semilinear parabolic equation［J］．JMath Anal Appl，1990，151:58-79．

［6］ Dai Q Y，Gu Y G．A short note on quenching phenomena for semilinear parabolic equations［J］．J Differential Equations，1997，137:240-250．

［7］ Dai Qiuyi．Quenching phenomena for quasilinear parabolic equation［J］．Acta Math Sinica，1998，41:87-96．

［8］ Salin T．On quenching with logarithmic singularity［J］．Nonlinear Analysis，2003，52:261-289．

［9］ 孙仁斌，胡军浩．含有对数奇异项的抛物方程解的整体存在性与猝灭性［J］．江西师范大学学报:自然科学版，2006，30(4):307-311．

［10］ Ferreira R，Pablo A，Quirós F，et al．Non-simultaneous quenching in a system of heat equations coupled at the boundary［J］．Z Angew Math Phys，2006，57:586-594．

［11］ Pablo A，Quirós F，Rossi JD．Non-simultaneous quenching［J］．Appl Math Lett，2002，15:265-269．

［12］ Zheng Sining．Non-simultaneous versus simultaneous quenching in a coupled nonlinear parabolic system［J］．Nonlinear Analysis，2008，69:2274-2285．

［13］ Pao C V．Nonlinear parabolic and elliptic equations［M］．New York:Plenum Press，1992．