尺度因子自适应的UKF算法在目标跟踪中的应用

侯建华，刘 倩，笪邦友，马晓路

(中南民族大学电子信息工程学院，武汉430074)

在目标跟踪领域，当系统的状态方程和观测方程是线性时，普通的卡尔曼滤波可以达到较好的跟踪效果［1］.而在实际应用中，现实背景复杂多变，导致系统方程或观测方程往往是非线性的，因此若采用线性的卡尔曼滤波跟踪，就会变得不稳定甚至发散，导致跟踪失败.传统的解决非线性估计问题的方法是采用扩展卡尔曼滤波器，1995年，Baumberg等提出了基于扩展卡尔曼滤波(EKF)的跟踪方法［2］.该算法是对非线性的系统方程或观测方程进行泰勒展开，取其一阶近似项，这种把非线性问题线性化的处理会不可避免地引入线性化误差，此外，系统方程或观测方程的Jacobian矩阵计算非常复杂、耗时，影响整个算法的实时性.为了解决此问题，Julier等提出了用Unscented卡尔曼滤波器来解决非线性滤波的问题［3］.Unscented卡尔曼滤波的核心部分是Unscented变换，它采用一组精心选择的加权采样点(Sigma)来表达系统的统计特性，这些采样根据真正的非线性方程进化而无需将其线性化.研究表明，UKF 算法与 EKF 算法［4，5］相比，能够为卡尔曼滤波器提供更好的非线性均值和方差近似解，对系统状态的估计精度和稳定性都有不同程度的提高.

本文在传统UKF对称采样策略的基础上，引入了比例修正框架［6］以保证协方差的半正定性，减少非局部效应的发生.此外，UKF采样过程中，传统的设定尺度因子的方法是根据实时的环境人工的调整尺度因子α，以得到最优经验值.为了提高UKF跟踪算法的实际应用性和智能性，有必要研究一种更优的自适应的尺度因子调整方法.因此，本文将一种尺度因子自适应的UKF算法应用于不同场景的目标跟踪中，实验证明该算法具有很好的跟踪性能和实用性.

1 Unscented变换

Unscented变换是计算非线性变换的随机变量的统计特征的一种新方法，它使用一组适当选择的带权重的离散采样点(Sigma点)来表征系统状态概率密度的均值和方差.U具体实现步骤是:把被估计的状态视为一个随机变量，在原先状态分布中按照某种采样策略［7］采样一些点，使这些点的均值和协方差与原状态分布中的均值和协方差相同，然后将非线性变换作用于每一个采样，得到相应的函数值点集，再求取这些点集的均值和方差，最后通过观测值调节样本点的位置，使采样点集的均值和方差以二阶精度逼近原状态的均值和方差.

假设n是随机变量x的维数，x的均值为¯x，协方差为Px，y=f(x)是一个非线性函数，通过Unscented变换估计随机变量y的均值和协方差的过程如下［8，9］.

(1)根据以下方程确定一组随机采样点Xi和采样点所对应的均值权值W(tm)和方差权值W(ic):其中κ是自由参数，用来捕捉给定分布的高阶矩信息，一般对于高斯分布，考虑到4阶矩的统计量，通常取n+κ=3.α是尺度因子，控制采样点和均值¯x之间的距离.β是用于考虑分布的先验知识［10］，通常取是矩阵平方根的第i列.

(2)根据非线性变换Yi=f(Xi)计算随机变量Yi的采样.

(3)计算随机变量Yi的均值和协方差:这里列出的Unscented变换是采用对称采样策略，文献［6］证明y均值的计算精度可以精确到三阶，对于协方差的精度可以精确到二阶.在利用公式(5)求权值时加入了比例修正(1－α2+β)，确保输出y的协方差的半正定性［11］.在目标跟踪算法中，就是用这些离散采样点来表征目标状态的.

2 尺度因子α的自适应方法

文献［3］证明可以通过调整尺度因子α的值来控制采样点到中心点的距离di，在对称采样方式下的该距离越远相应的采样点的参考价值就越小，即会产生非局部效应.在仿真实验时可以通过对α取不同的值，从中选择最优的值以达到最好的跟踪效果.但在实时环境中，不允许尝试，必须给出一个具体的尺度因子的取值方案.所以，参考文献［12］，本文将尺度因子α随环境自适应变化的算法应用于UKF的目标跟踪.

假设t时刻的UKF滤波值为x^t/t，真实值为xt/t，而由公式(9)可知，Pt/t表征了预测值与真实值的关系(也就是误差)，可以近似的计算出x^t/t与xt/t之间的距离dt/t，为了方便计算，利用公式(10)近似计算dt/t:

这种方法的基本思路就是用第k步的滤波值近似覆盖真值的邻域O(^xt/t，dt/t)，此作为第t+1样范围，使Sigma点(采样点)到中心点的距离di不超过dt/t，即令:

利用公式(11)求出的 αt+1/t，重新采样生成Sigma点和相应的权值，完成相应的更新.这样循环的更新的 α值，就可以得到尺度因子自适应的Unscented变换.

3 UKF对跟踪系统的建模

UKF是在普通卡尔曼滤波的框架上，将Unscented变换分别应用于均值和协方差的求解，并不断递推，就可得到UKF非线性滤波器.

考虑一般的目标跟踪问题，目标的状态方程和观测方程分别为:

其中A为表征运动模型的参数，xt表示t时刻系统的状态向量，zt为时刻的观测向量，vt为系统噪声，ωt为观测噪声.

本文UKF滤波过程的实现步骤如下:

1)初始化，根据初始状态变量x得到均值^x和协方差P0.

2)计算2n+1个加权Sigma点xi(t－1/t－1)来表征系统的状态分布(其中i=0，1，…，2n，是状态向量的维数):

得到采样点集xi(t－1/t－1);根据公式(9)～(11)更新α;最后将更新的αt+1/t代入公式(4)～(7)计算相应的权值W(m)i，W(c)i.

3)预测.由系统状态方程和观测方程对各个采样的Sigma点集里的每个采样点进行非线性变换，得到变换后的Sigma点集:

计算预测的状态均值和协方差:

4)观测更新.计算观测均值、自相关函数和观测的互相关函数:

计算状态更新的滤波增益:

状态更新后的滤波值:

状态后验概率方差阵:

若继续跟踪t=t+1，转(2);否则结束.

4 仿真方案

为了验证尺度因子自适应的UKF跟踪算法的效果，分别对传统的UKF算法和自适应的UKF算法进行了仿真，并对新算法的实用性进行了测试.

4.1 算法的自适应性验证

4.1.1 仿真条件

在二维直角坐标系中，假设目标做匀速运动，取目标的位置和速度为系统的状态变量，即→x=［x，y，vx，vy］，x和y表示目标中心点的坐标，vx，vy分别表示x，y的导数，即速度.观测向量zt的两个分量分别表示t时刻目标中心处的斜距和方位角，xct和yct分别表示t时刻目标中心处的观测值.vt是从传感器得到的噪声，ωt是从观测样本得到的噪声(仿真时加入随机噪声以模拟复杂环境).具体仿真条件如下:

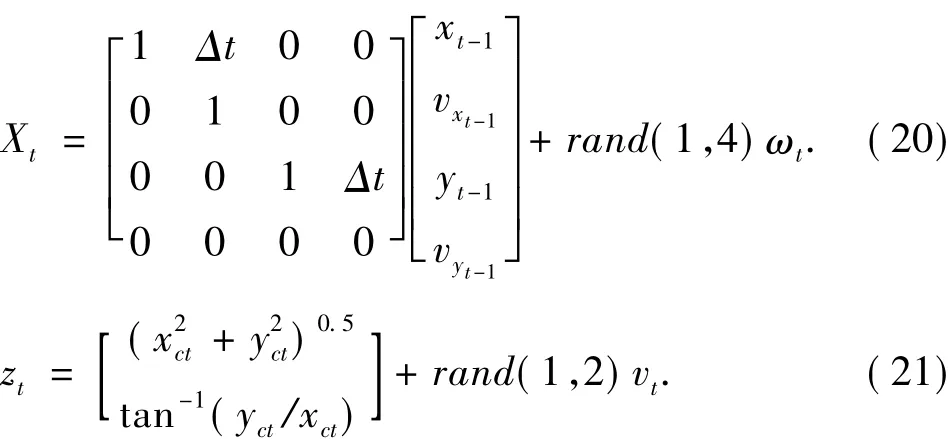
初始状态向量→x0=［15000，30，15000，30］，Δt=10是采样间隔.

4.1.2 仿真结果与分析

首先对标准的UKF算法进行仿真，分别取α为0.1，0.3，0.5，0.8，1(其中 α=1 是为最优经验值).其次，对本文提出的尺度因子α自适应的UKF算法进行仿真.

实验结果如表1.表1中真值与UKF滤波值的误差比公式为:

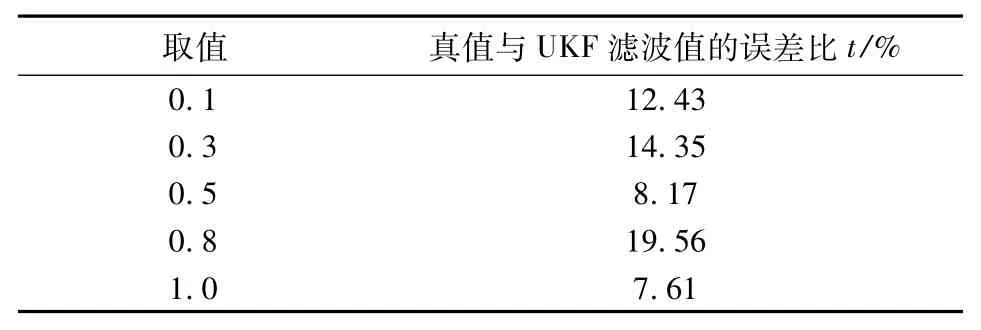
表1 不同α下的跟踪精度Tab.1 Tracking performance with difference α

从表1可以看出，尺度因子α的不同取值时对跟踪精度有很大的影响，滤波精度有明显的差异，因此实际应用时需要人工反复调节α的大小以获得最优值(α=1)，使真值和滤波值的差异最小.此操作复杂，智能性和实用性不高.

图1(a)和图1(b)对比可知，尺度因子α自适应的UKF算法能够取得和最优经验值(α=1)时的UKF算法基本相同的跟踪精度.

图1 不同α下的跟踪精度Fig.1 Tracking performance with difference α

4.2 算法的实用性验证

4.2.1 实验条件

为了测试本文算法的实用性和智能性，本文分别对动态背景下的行人行走视频(实验一)和多干扰复杂环境下的车辆行驶视频(实验二)进行试验，并将仿真结果与卡尔曼滤波的跟踪算法进行对比.两组实验的状态向量设置为二维空间的目标的位置、速度，即→x=［x，y，vx，vy］，状态初始值由手动选取目标区域完成，考虑到实时视频任意相邻两帧帧差为几十毫秒，目标速度基本不会发生变化，所以设置系统运动模型为匀速即状态转移矩阵:

A=［1，1，0，0;0，1，0，0;0，0，1，1;0，0，0，1］T，观测模型参数为t时刻目标中心处的斜距和方位角，如公式(21)，系统噪声和观测噪声均调到最佳.

4.2.1 实验结果与分析

如图2所示，本组实验是在视频第三帧时，人工的选取要跟踪的目标(也就是确定初始状态值)，黑色矩形框是目标的跟踪框.视频中的树木和其他行人构成了变化的背景，地面颜色与选定的目标人物上衣颜色相仿，图2(a)～(c)中，由于动态背景和周围杂物的影响，普通的卡尔曼跟踪算法在第30帧时跟踪框已经逐渐偏离目标，在第60帧时已经无法对目标进行跟踪.而图2(d)～(f)(本文算法实验结果)具有明显的优势，在动态背景环境下，本文算法却仍然能够稳定地跟踪目标.

(1)普通卡尔曼滤波进行人体跟踪结果如图2(a)～(c);本文算法进行人体跟踪结果如图2(d)～(f).

图2 卡尔曼滤波和本文算法的比较Fig.2 Comparisons between Kalman filter and improved UKF

(2)普通卡尔曼滤波进行交通车辆跟踪结果如图3(a)～(c);本文算法进行交通车辆跟踪跟踪结果如图3(d)～(f).

图3 卡尔曼滤波和本文算法的比较Fig.3 Comparison between Kalman filter and improved UKF

图3是普通卡尔曼滤波和本文算法用于监测交通车辆的实验结果，初始状态也是通过人工选取，即图3(a)中的第5帧和图3(d)中的第2帧中黑色矩形框选定的卡车.视频中其他来往的车辆构成复杂的非线性背景.实验表明，在复杂的非线性环境下，普通卡尔曼算法不能达到跟踪的目的，如图3(b)所示，在视频第10帧时黑色跟踪框已经偏离目标，基本上失去了跟踪的意义.而本文算法如图3(f)所示，可以一直很稳定的对目标进行跟踪，具有很好的跟踪效果.

综合图2和图3可以看出，不同场景条件下，不用人为的调节尺度因子，本文算法都具有很好的跟踪效果，自适应能力很强，实用性很好.

5 结语

本文提出的尺度因子自适应的UKF跟踪算法能够取得和最优经验值条件下的普通UKF算法大致相同的精度;在不同的实际环境下都能取得理想的跟踪效果，提高了非线性滤波的实时跟踪能力和滤波的数值稳定性，具有非常好的实用价值.

［1］付东莉，柴 毅.基于滚动时域估计的带约束运动目标跟踪［J］.计算机应用研究，2011，28(3):1-3.

［2］Baumberg A，Hogg D C.Learning spatiotemporalmodels from training exemples［C］//Proc.British Machine Vision Conference.Birmingham:Proc，1995:45-74.

［3］Simon J.Julier，Jeffrey K.unlmann.A new extension of the kalman filter to nonlinear systems［C］//Proc.The 11th International Symposium on Automatic Control，Aerosense:Proc，2000，21(45):447-482.

［4］Zhu Anfu，Jing Zhanrong.UKF and its application to target tracking［J］.Fire Control and Command Control，2008，33(8):2-3.

［5］Mathicu ST-Pierre，Denis Gingars Dr Ing.Comparison between the unscented kalman filter and the extended kalman filter for the position estimation module of an intergrated navigation information system［J］.IEEE Intelligent Vehicles Symposium University of Parma，2004，34(7):832-834.

［6］Julier S，Unlmann J，DurrantWhf.A new method for the nonlinear transformation ofmeans and covariance in filters and estimators［J］.IEEE Transactions on Automatic Control，2000，45(3):477-482.

［7］刘 铮.UKF算法及其改进算法的研究［D］.长沙:中南大学，2009:25-28.

［8］Julier S J，Uhlmann JK.Reduced sigma point filters for the propa-gation of means and covariance through nonlinear transformations［C］.//Proc.American Control Conf.Jefferson:Proc，2002:887-892.

［9］Yong Rui，Chen Yunqiang.Better proposal distributions:object tracking using unscented particle filter［J］.Computer Vision and Pattern Recognition，2001，10(21):47-51.

［10］MOSHE BEN-ALIVA.Nonliner kalman filtering algorithms for on-line calibration of dynamic traffic assignmentsmodels［J］.IEEE Transaction on Intelligent Transportation Systems，2007，8(4):664-665.

［11］Julie S J.The scaled unscented transformation［C］//Proc.American Control Conf.Jefferson:Proc，2002:4555-4559.

［12］Jiang Weinan，Zhou Haiyin.Self-adaptive selectingmethod for scaling factor of scaled unscented transformation［J］.Chinese Space Science and Technology，2008，6(3):3-5.