正态云隶属度函数确定的FSM方法

刘 琪 刘晓青

(周口师范学院物理与电子工程系，河南 周口 466001)

正态云隶属度函数确定的FSM方法

刘 琪 刘晓青

(周口师范学院物理与电子工程系，河南 周口 466001)

隶属度函数及其确定方法的研究具有重要意义。采用正态云模型表示的隶属度函数综合了模糊性和随机性，具有普适性;提出了确定隶属度函数的模糊减法均值聚类(FSM)方法，得到了最优聚类中心和数据的隶属度。实例仿真表明，采用该方法确定了石油钻井中总体积的正态云隶属度函数，解决了隶属度函数难以客观描述和难以确定的问题。

正态云模型 隶属度函数 不确定性 模糊减法均值聚类 石油钻井

0 引言

在客观世界的不确定性中，特别是在人类思维和认知载体的语言中，随机性和模糊性存在极大的关联性［1-3］。李德毅在随机数学和模糊数学的基础上，提出用正态云模型来描述不确定性现象与事物的随机性、模糊性及其关联性［4］。然而隶属度函数的确定方法一直没有得到根本解决。在不确定性推理过程中，隶属度函数往往是被主观取值“硬化”成区间［0，1］中的精确数值表达，不考虑随机性，且不具有模糊性和可靠性。

本文采用正态云模型表示隶属度函数，提出了模糊减法均值聚类(fuzzy subtractive means clustering，FSM)方法，确定了石油钻井中总体积变化量的正态云隶属度函数［5］，解决了隶属度函数难以客观描述和难以确定的问题。

1 正态云隶属度函数

正态云模型是定性概念与定量表示之间的不确定性转换模型，它表征了知识表示中的模糊性(边界亦此亦彼)和随机性(发生的概率)。

定义1［1］设U为一个用精确数值表示的定量论域，C为U上的定性概念，若定量值x∈U，且x是定性概念C的一次随机实现，x对 C的隶属度 μ(x)∈［0，1］是有稳定倾向的随机数，则称μ(x)在U上的分布为云模型。设N(A，B)表示服从正态分布的随机函数，其中A为期望值，B为标准差，则有:

式中:Ex为期望值;En为熵;He为超熵。式(1)～式(3)表示变量μi与xi之间的函数关系。满足式(1)～式(3)的数据对 drop(xi，μi)(i=1，2，…)构成的云模型称为正态云模型，记为(Ex，En，He)，正态云模型的数学特征和贡献如图1所示。

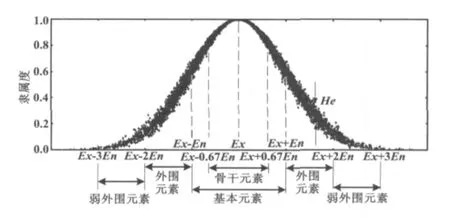
图1 数学特征和贡献Fig.1 Mathematical characteristics and contribution

正态云模型分为期望值Ex、熵En、超熵He这几个数学特征值。

期望值Ex是指概念在论域中的中心值，其在论域空间中最能够代表定性概念。期望值Ex隶属于定性概念。

熵En是指定性概念模糊度的度量，代表一个定性概念的可度量粒度，即在论域中可被概念所接受的数值范围，通常熵越大，概念所接受的数值范围也越大，概念越模糊。熵En体现了定性概念亦此亦彼的裕度。

超熵He是指熵En的熵，反映了云滴的离散程度，是熵的不确定性的度量。超熵越大，隶属度的随机性越大，云的厚度越大。超熵He反映了定性概念值的样本出现的随机性，揭示了模糊性和随机性的关联。当He=0时，正态云模型退化为其期望曲线:

定义2［6］云中的任一区间 x∈［a，b］上元素对定性概念~A的贡献C为:

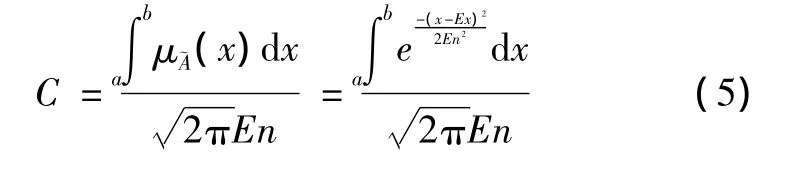
由此可知:①对于整个论域x∈(-∞，+∞)，C=1，全部元素对定性概念~A的贡献为100%;②对于x∈［Ex-0.67En，Ex+0.67En］，C=0.5，这部分元素对定性概念的贡献~A为总贡献的一半，称为“骨干元素”;③对于x∈［Ex-En，Ex+En］，C=0.683，这部分元素对定性概念的贡献~A为总贡献的68.3%，称为“基本元素”。

随机变量y的概率密度函数为:

随机变量y的概率密度同云的三个数学特征无关。这说明对于定性概念，云滴有确定的统计分布，其不确定性中仍然包含确定的规律性，反映了人们对知识表示定性概念的共同性。

正态云模型综合表征了不确定性的模糊性和随机性，是定性概念与定量表示之间的不确定性转换模型，具有普适性。采用正态云模型的隶属度函数具有以下特点。

①云由大量的云滴组成，一个云滴是定性概念在数量上的一次实现，云的整体形状反映了隶属度函数的基本特征，云滴数目表示了云对定性概念的贡献。

②云的厚度是不均匀的，其在腰部最分散、厚度最大，而顶部和底部的汇聚性好、厚度小。云的厚度反映了隶属度随机性的大小，越靠近概念中心或远离概念中心的隶属度，其随机性越小，与人的主观感受一致。

③所有x∈U到区间［0，1］的映射均为一对多，隶属度是正态概率分布，隶属度的细微变化产生了云。

2 模糊减法均值聚类方法

模糊聚类分析是许多分类和系统建模的基础［7］。聚类的目的是从大量的数据中抽取固有的特征，以获得系统行为的简洁表示。Bezdek提出的用隶属度确定数据点属于某个聚类程度的模糊C均值聚类(fuzzy c-means clustering，FCM)方法［8-9］，其适应性强，是目前比较成熟的模糊聚类方法;但FCM方法要求首先提供聚类中心个数，且严重依赖随机生成的初始聚类中心。

对于 X={x1，x2，…，xn}⊂RS的样本点集合，模糊减法均值聚类(FSM)方法如下。

① 设定聚类参数，包括邻域半径ra、比例参数δ、模糊指数m和容许误差Emax，计算每一个点xi的密度指标 Di。

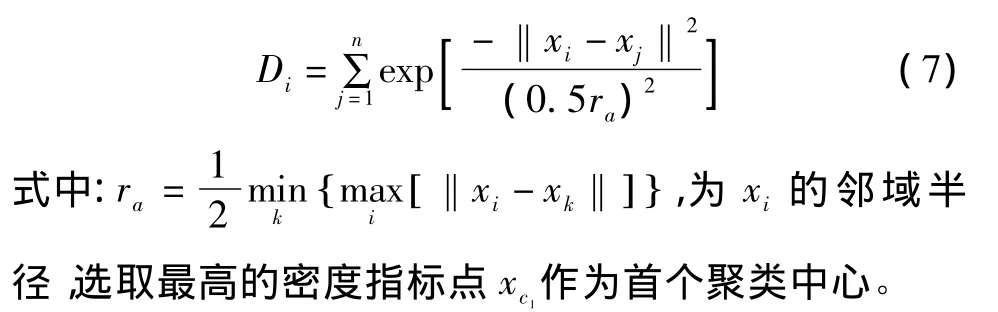
②对每个数据点的密度指标进行修正。

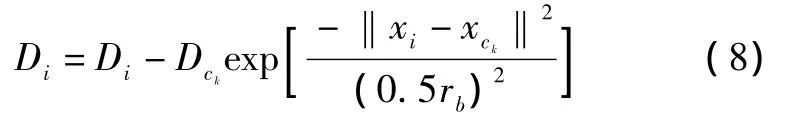
式中:rb为密度指标函数显著减小的邻域半径，一般为rb=1.2ra，取最高的q个密度指标点xck+1作为新的聚类中心 wk(l)，其中，l=1;k=1，2，…，q。

③判断。

判断式(9)是否成立，若不成立，返回步骤②。

④ 计算xi对wk(l)的隶属度uik。

⑤调整聚类中心。

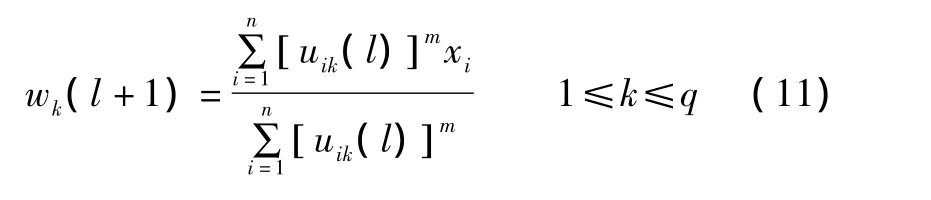
⑥ 计算价值函数J(l)和误差δ:

如果δ＜Emax，结束迭代，并输出聚类结果;否则l=l+1，返回步骤④。

3 实例仿真

通过模糊减法均值聚类(FSM)方法，可以得到聚类中心和每个数据点对聚类中心的隶属度，这些参数可以确定正态云隶属度函数。本文的实例选用鄂北石油钻井现场总体积数据EB_Da51中的200个数据［10］，其分布如图2所示。

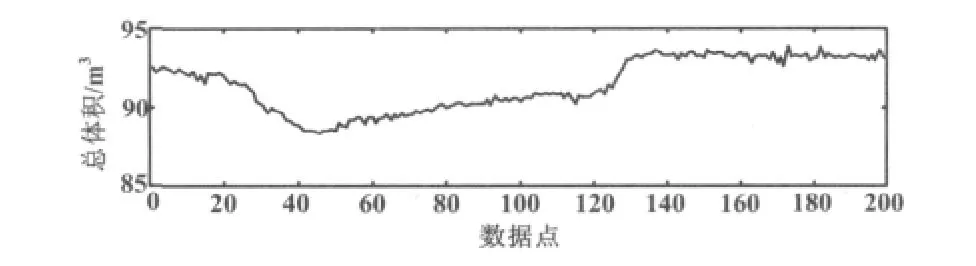
图2 石油钻井中的总体积Fig.2 Total volume of petroleum drilling

采用FSM方法确定总体积变化量的正态云隶属度函数，其具体步骤如下。

①数据统一论域，求解总体积的变化量并将其映射到统一论域空间。

②模糊减法均值聚类(FSM)，求解聚类中心wk、聚类中心个数q和数据对聚类中心的隶属度uik。

③确定语言值和每个语言值的期望值Exk(1≤k≤q)。本实例中q=4，取无、小、中、大四个语言值，通过FSM方法得到的聚类中心即为每个语言值对应的正态云模型的期望值Exk。

④确定每个语言值的熵Enk(1≤k≤q)，用正态云模型的期望曲线逼近200个样本点的隶属度uik构成的曲线，即求解满足式(14)的目标函数最小的Enk。

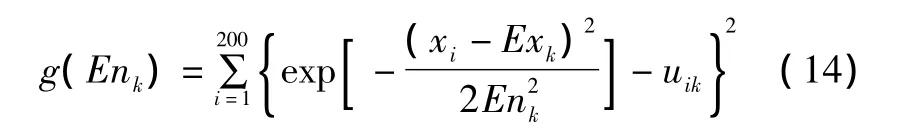
⑤确定每个语言值的超熵Hek。超熵Hek的确定比较困难，一般由专家根据具体情况而定，本文给出一种近似求法。

采用上述方法得到的总体积变化量的q个语言值的Ex、En和He如表1所示。

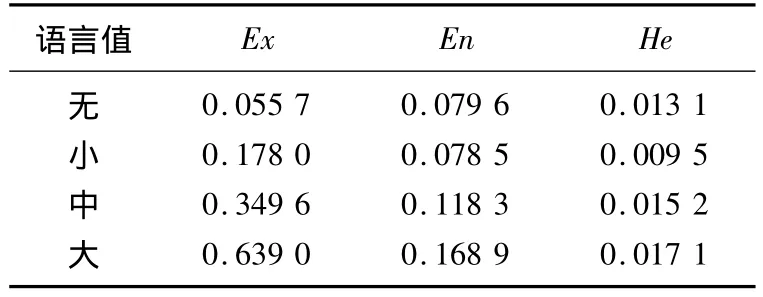
表1 总体积变化量的数学特征Tab.1 Membership function of the variable quantity of the total volume

根据表1中的语言值参数，可得到总体积变化量的正态云隶属度函数，如图3所示。

4 结束语

实例研究表明，模糊减法均值聚类方法迭代次数少、收敛速度快、运算稳定，避免了模糊C均值聚类方法需要首先确定聚类中心个数的盲目性和陷入局部极小点的可能性。采用FSM方法确定的正态云隶属度函数综合表征了数据的模糊性和随机性，解决了隶属度函数难以客观描述和难以确定的难题。

［1］李德毅.知识表示中的不确定性［J］.中国工程科学，2000，10(2):73-79.

［2］Fred A.Applications of AI and soft computing for challenging problems in the oil industry［J］.Journal of Petroleum Science and Engineering，2005，47(1-2):5-14.

［3］陆建江，张亚非，宋自林.模糊关联规则的研究与应用［M］.北京:科学出版社，2008:43-51.

［4］李德毅，孟海军，史雪梅.隶属云和隶属云发生器［J］.计算机研究与发展，1995，32(6):51-20.

［5］王杰，陈东海，朱晓东，等.基于分层模糊系统的石油钻井事故预警系统［P］.中国，200710055178.6，2007-9-18.

［6］罗自强，张光卫，李德毅.一维正态云的概率统计分析［J］.信息与控制，2007(8):471-475.

［7］陈铁梅.模糊聚类在数据预处理中的应用研究［J］.自动化仪表，2008，29(5):36-37，41.

［8］刘琪，张鸿辉，黄贞贞.基于模糊C-均值聚类方法的石油钻井工作状态分析［J］.周口师范学院学报，2009(5):47-49.

［9］张勇，张凤登，陈小荣.客流统计系统中的FCM算法研究［J］.自动化仪表，2010，31(3):26-28.

［10］刘琪，王少辉.非线性隶属度函数确定的单次聚类方法［J］.周口师范学院学报，2011(2):41-42.

Membership Function of the Normal Cloud Determined by FSM Method

The research on membership function and its determination method has great significance.The membership function presented by adopting normal cloud integrates fuzzy and random performances，and possesses common adaptability.The method of fuzzy subtractive means clustering(FSM)is proposed for determining the membership function for obtaining optimal clustering center and membership degree of data.In practical simulation，the membership function of normal cloud for the total volume in petroleum drilling is determined and the difficulty of describing and determining the membership function has been solved.

Normal cloud modelMembership function Uncertainty Fuzzy subtractive means clustering(FSM)Petroleum drilling

TP181

A

河南省教育厅自然科学研究计划基金资助项目(编号:2011B510021);

周口师范学院教学改革研究基金资助项目(编号:J2010072)。

修改稿收到日期:2011-01-17。

刘琪(1983-)，男，2010年毕业于郑州大学控制理论与控制工程专业，获硕士学位，讲师;主要从事控制理论与应用、智能控制与模式识别方面的研究。