解排列组合问题的“几先几后”

☉山东省日照实验高级中学 孙先进

解排列组合问题的“几先几后”

☉山东省日照实验高级中学 孙先进

学生在求解排列组合问题时，最常犯的错误是分类、分步不清，重复或遗漏计数等，且这些错误的发生不易被检验出来，造成这种现象的原因是对解决排列组合问题的相关策略没有理解到位，下面提出几种策略，供参考.

一、先考虑分类，后考虑分步

对排列组合问题的设置，经常伴有一些约束条件，解决这类问题应先按元素性质进行分类，再按事情发生的连续过程分步处理.

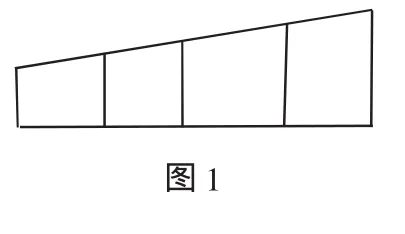
例1 如图1，用6种不同的颜色给图中的4个格子涂色，每个格子涂一种颜色，要求最多使用3种颜色且相邻的两个格子颜色不同，则不同的涂色方法共有____种.（用数字作答）

解析：由题意可分两类：

二、先考虑顺序后考虑计算

两个计数原理是解决此部分内容的重要工具，元素是否重复，有无顺序，是判断一个问题的解决是用计数原理还是用排列组合数公式的依据.

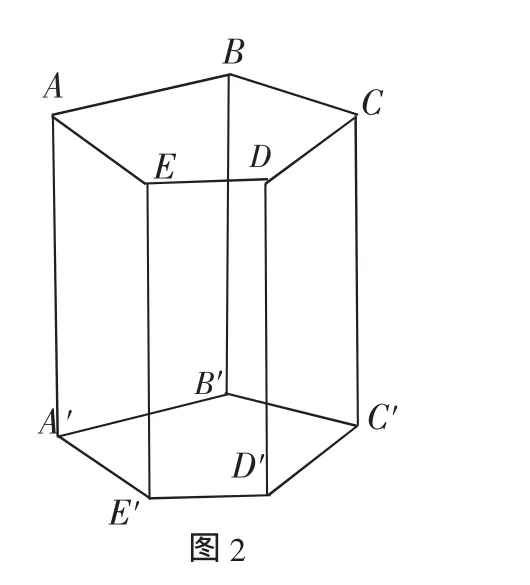
例2 已知正五棱柱ABCDEA′B′C′D′E′（如图2），现从10个顶点中任意取5个顶点，则可组成多少个不同的四棱锥？

错解：（1） 第一步，从A、B、C、D、E中任意取4个点组成四棱锥的底面，有5种不同的方法；

（2）第二步，从A′、B′、C′、D′、E′中任意取1个点组成四棱锥的顶点，有5种不同的方法.由分步乘法计数原理，不同的取法共有N＝5×5＝25（种）.

同理，从A′、B′、C′、D′、E′中任意取4个点组成四棱锥的底面，从A、B、C、D、E中任意取1个点组成四棱锥的顶点，也有25个.

所以共有50个不同的四棱锥.

剖析：四棱锥的特点是其中底面四个顶点在同一平面内，另一点不在平面内即可.而错解中忽略了例如A、B、A′、B′，A、C、C′、A′，A、B、E′、C′等也在同一平面内的情况.

正解：在错解的基础上，另外还有以ABA′B′为底面，从C、D、E、C′、D′、E′中任取一点为顶点，有6个四棱锥.同理，以BCB′C′、CDC′D′、DED′E′、AEA′E′为底面分别有6个四棱锥，则共有30个四棱锥；以ACC′A′为底面，从B、E、D、B′、E′、D′中任取一点为顶点，有6个四棱锥，同理，以BDD′B′、CEE′C′、DAA′D′、EBB′E′为底面分别有6个四棱锥，则共有30个四棱锥；以ABE′C′为底面，从C、D、E、A′、B′、D′中任取一点为顶点，有6个四棱锥.同理，以BCD′A′、CDE′B′、DEA′C′、EAB′D′、A′B′EC、B′C′DA、C′D′EB、D′E′AC、E′A′BD为底面分别有6个四棱锥，则共有60个四棱锥.所以共有N=25+25+30+30+60=170（个）.

共有170个不同的四棱锥.

三、先考虑定性，后考虑定量

当题目的条件比较笼统、不明确时，一般应先分好明确的类别或者步骤，再用相应的原理解决.

例3 从5名男生和4名女生中任选3人，要求至少有男生和女生各一人的选法有（ ）种.

A.70 B.140 C.84 D.35

剖析：事实上，不妨设5名男生分别为甲、乙、丙、丁、戊，4名女生分别为A、B、C、D.当先分别选1名男生和1名女生时，选到了男甲女A，再在剩下的7人中任选1人时，选到了男乙，从而选到三人的一种方式为男甲女A男乙.当先分别选1名男生和1名女生时，若选到了男乙女A，再在剩下的7人中任选1人时，选到了男甲，这时选到三人的一种方式为男甲女A男乙.这两种方式是同一种选法，因此，上述解法中有重复现象，从而是错误的.要想正确解答该题，关键在于应对题设条件“至少有男生和女生各一人”给出具体的分类，明确到底有几名男生，几名女生.

正解：完成事件分为两类：选1名男生、2名女生和选2名男生、1名女生.

四、先考虑特殊，后考虑一般

某些排列组合问题中带有特殊元素或特殊位置的排列组合题，对此类问题的处理一般应先考虑特殊情况，本着特殊者优先的原则处理.

例4 用0到9这10个数字，可以组成没有重复数字的三位偶数的个数为（ ）.

A．324 B．328 C．360 D．648

解析：因为“0”是特殊元素，它不能排在最前面，所以分两种情况考虑.

因此由分类计数原理，符合题意的偶数共有72+256=328（个）.故选择B.

对于受限制的特殊元素（或位置）的排列组合问题，要先安排“特殊”元素（或位置），再安排其他没有限制的元素或位置.因此特殊元素（位置）用优先法.

例5 某地奥运火炬接力传递路线共分6段，传递活动分别由6名火炬手完成．如果第一棒火炬手只能从甲、乙、丙三人中产生，最后一棒火炬手只能从甲、乙两人中产生，则不同的传递方案共有________种．

五、先考虑组合，后考虑排列

对于排列组合的混合问题，一般采取先选出元素即分组，再进行排列的原则解决问题.

例6 将4个不同的小球放入编号为1、2、3、4的四个盒子中，则恰有一个空盒的方法有_______种.

解析：这是一个排列组合的混合问题.因恰有一个空盒，所以必有一个盒子要放2个球.故可分两步进行.第一步，先分组.从4个球中任选2个球，有种选法，从4个盒子中选出3个，有种选法.

第二步，进行排列.把选出的2个球视为一个元素，与其余的2个球共3个元素对选出的3个盒子作全排列，有种排法.

六、先考虑总体，后考虑个体

例7 在某种信息传输过程中，用4个数字的一个排列（数字允许重复）表示一个信息，不同排列表示不同信息，若所用数字只有0和1，则与信息0110至多有两个对应位置上的数字相同的信息个数为（ ）.

A.10 B.11 C.12 D.15

解析：此题用直接法进行分类求解较为复杂，故想到排除法，先求出与0110有三个位置或四个位置上的数字相同的排法，再用允许数字重复的总排列数相减即可.用0和1进行排列，允许数字重复共有16种排法，因为与0110有三个位置上的数字相同的排法有四种：1110、0010、0100、0111，与0110有四个位置上的数字相同的只有一种排法，所以与信息0110至多有两个对应位置上的数字相同的信息个数有16-4-1=11（种）.故选择B.

有些问题从正面直接考虑比较复杂，而从它的反面往往比较容易思考时，可以先求出它的反面，再从整体中排除.因此至少或至多问题应采用排除法.