矩阵K dV约束流的r矩阵

徐 英，梁凤鸣

(1.淮南师范学院数学与计算科学系，安徽淮南 232001;2.泰山学院学报编辑部，山东泰安 271021)

1 引言

近几十年来，著名的r矩阵理论［1］被广泛的应用于研究约束孤子流中，这些约束孤子流是由孤子方程通过非线性化Lax对文献［2－3］得到的有限维经典可积Hamilton系统.又因为所有这些约束孤子流都有Lax表示Lx=［U，V］，其中L和V都是李代数.因此，其守恒积分可以由TrLk，k∈Z表示.由如下r矩阵关系

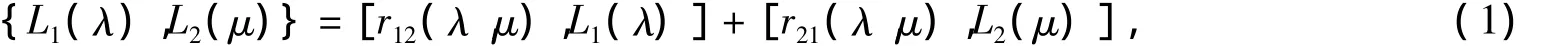
通过直接计算，可以得到如下对合关系

已有的r矩阵关系几乎都是在对2×2矩阵型的Lax算子的研究中得到的［4－6］，在本文中我们考虑一个4×4矩阵型的Lax算子的r矩阵关系，我们会发现这个Lax算子也满足r矩阵关系(1)，从而有(2)，由此我们可以得到其有限维Hamilton系统足够多的守恒积分在Poisson括号下两两对合，进而可证明其有限维Hamilton系统在Liouville意义下是完全可积的.

2 矩阵KdV方程

文献［7］考虑4×4谱问题

其中

以及(3)的辅助谱问题

其中

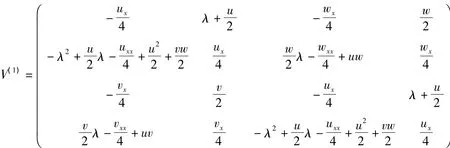
的Lax对非线性化.

3 有限维可积系统的r矩阵

文献［7］考虑(3)和(4)的Lax对非线性化.

在约束

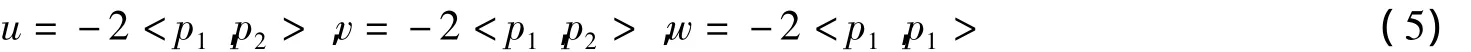
下，得到其有限维Hamilton系统

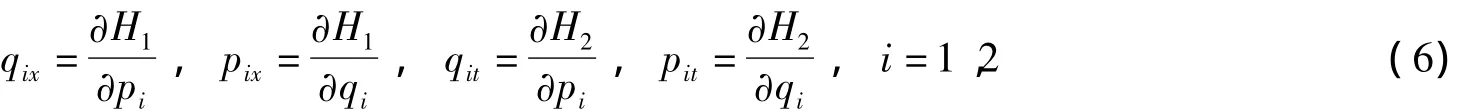
其中

有限维Hamilton系统(6)有如下Lax表示

当且仅当约束(5)成立，这里

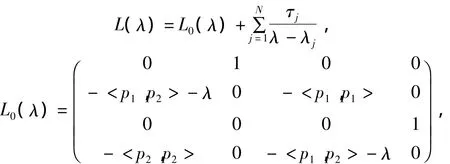
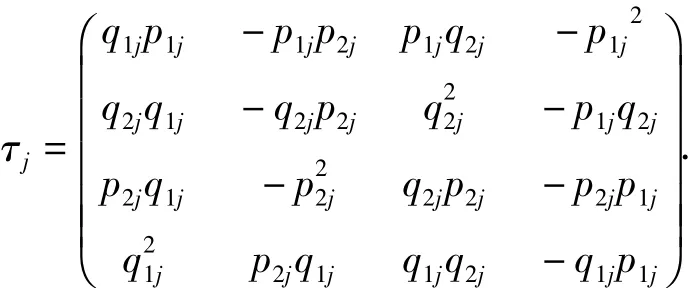
在辛流形(R4N，∑2i=1dpi∧dqi)下，两光滑函数f，g的Poisson括号定义为

记L1(λ)=L(λ)⊗E4，L2(μ)=E4⊗L(μ).这里C=A⊗B定义为c4(i－1)+k，4(j－1)+ι=aijbkl，A=(aij)，B= (bkl)［8］.

在Poisson括号(8)下，通过复杂冗长的计算得到［8］

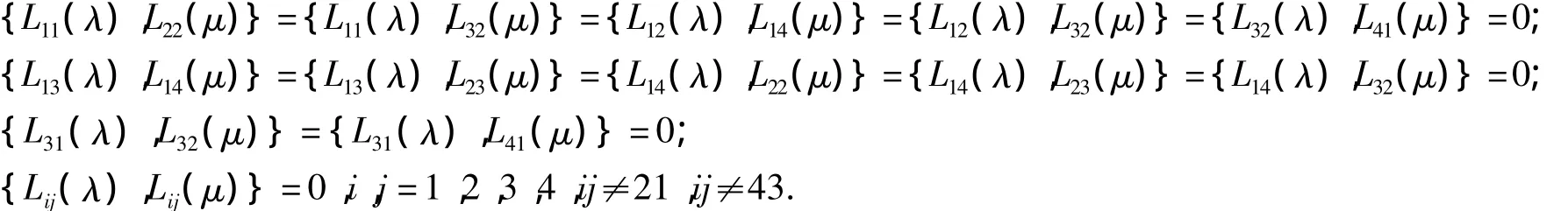
由此可得如下定理.

定理1 L(λ)满足r矩阵关系

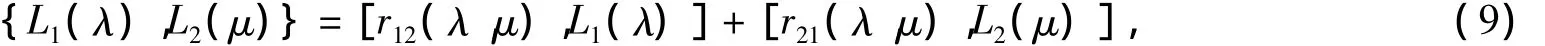
其中

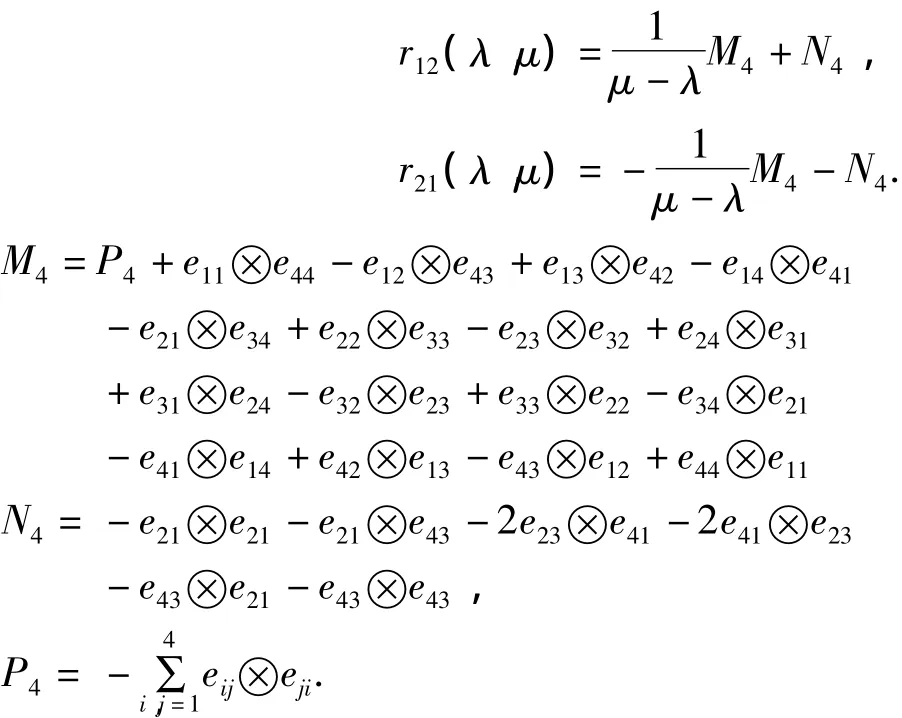
这里ekl为第k行l列元素为1，其他位置全为0的4×4矩阵.

由r矩阵关系(1)，有

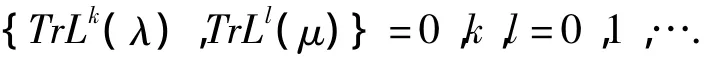
Lax矩阵的特征多项式是

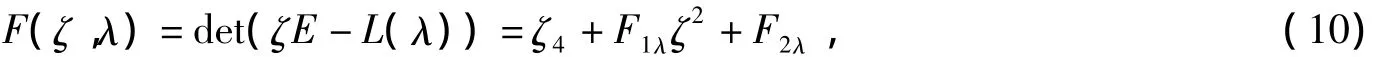
其中

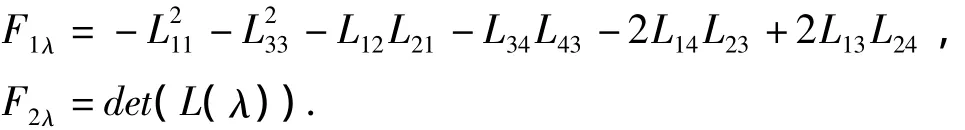
设

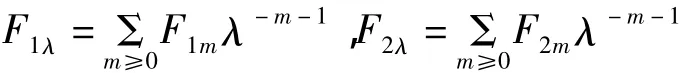
因此，Hamilton函数与守恒积分的关系可以表示成

并且由定理1可知，L(λ)满足r矩阵关系，所以(2)成立，从而守恒积分对合，即{Fim，Fin}=0，i，j=1，2.

又由文献［7］知守恒积分Fim(i=1，2，1≤m≤N)在R4N的稠密开子集上是函数独立的.因此，在辛空间中，该有限维Hamilton系统(6)在Liouville意义是下完全可积的.

［1］Babelon O，Villet CM.Hamiltonian structures and Lax equations［J］.Phys.Lett.B.，1990(237):411－416.

［2］Cao CW，Geng X G.Classical integrable systems generated through nonlinearization of eigenvalue problems［A］.Proc Conf on Nonlinear Physics(Shanghai1989)Research Reports in Physics［C］.Berlin:Springer，1990.

［3］Cao CW.Nonlinearization of the Lax system for AKNS hierarchy［J］.Science in China(A)，1990(33):528.

［4］Zhou R G.Dynamical r－matrices for the constrained Harry－Dym ows［J］.Phys.Lett.A.，1996，220(6):320－330.

［5］Zhou RG.r－matrix for the restricted KdV owswith the Neumann constraints［J］.Journal ofMathematical Physics，1998(2):181－189.

［6］陈金兵.广义c－KdV约束流的Lax对及其r矩阵［J］.徐州师范大学学报，2003，21(3):1－5.

［7］Qin Z Y.A nite－dimensional integrable system related to a new coupled KdV hierarchy［J］.Phys.Lett.A.，2006(53):1－8.

［8］Faddeev L D，Takhtajan.Hamiltonian methods in the theory of soliton［M］.Spring:Verlag，1987.