基于反馈线性化的车用无刷直流电机转矩随动控制

周 苏，王明强，陈凤祥

（1.同济大学汽车学院，上海，201804；2.同济大学新能源汽车工程中心，上海，201804；3.同济大学中德学院，上海，200092）

电动汽车的发展需要电机及其驱动系统的配套支持。作为众多电机类型中的一种，方波无刷直流电机（BLDCM）由于结构简单、维护方便、运行可靠、效率高、调速性能好等诸多优点而逐步受到重视［1－2］。但是，低速转矩脉动问题一直困扰直流无刷电机的应用推广［3］，尤其是在高精度调速及直接驱动应用场合，例如在电动汽车上通常要求电机系统的低速转矩脉动小于3%。更重要的是，传统的控制目标着眼于电机转速，而由于电动汽车驱动性能受地面附着力的限制，往往需要对车用驱动电机转矩直接进行控制，否则容易出现电机驱动滑转等问题。因此，寻求一种有效的转矩脉动抑制及转矩跟随控制策略是无刷直流电机应用于车辆驱动的关键步骤。

由于BLDCM系统具有非线性、强耦合等特征，传统的双闭环电流滞环控制策略无法有效抑制其低速转矩脉动［4－5］。文献［6］提出了一种抑制转矩脉动的重叠换相法，即导通相提前开通，关断相延迟关断，但其重叠区间大小难以确定。这些方法都只能在一定程度上抑制转矩脉动，且调节工作量大，无法从原理上解决目标转矩有效追踪问题。文献［7］分析了无刷直流电机在一个电周期内的转矩变化过程，并将其划分为12个工作区间，实际上指出了无刷直流电机运行过程中具有变结构的非线性特性。输入－输出反馈线性化是一种有效的非线性控制方法，其适用领域较广［8］。本文拟采取输入－输出反馈线性化的控制方法，分工作区间对无刷直流电机加以控制，以期有效抑制转矩脉动，获得良好的转矩随动性能。

1 车用无刷直流电机模型的建立与分析

1.1 电路模型

本文以常见的两相导通六状态三相无刷直流电机为研究对象，其系统结构如图1所示。

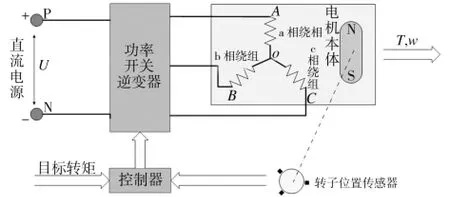
图1 无刷直流电机系统结构示意图Fig.1 Schematic diagram of BLDCMStructure

对任意一相绕组进行电路分析，由基尔霍夫电压定理得到端电势方程：

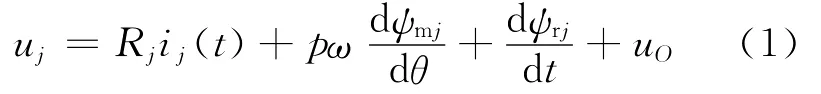
式中：j分别代表a、b、c三相；Rj为j相绕组电阻；uO为中性点电势；ij（t）为绕组电流；ψmj为永磁铁磁场磁链；ψrj为绕组感应磁链；θ为转子电角度；ω为转子转速，ω＝（dθ／dt）／p，其中p为磁极对数。记ej＝pωdψmj／dθ，一般称之为旋转反电动势，其系数kej＝pdψmj／dθ决定了反电动势的基本波形，而其系数幅值为常数ke。

建立电机模型时作如下假设：①三相绕组完全对称、均匀分布，这在电机绕组设计中是必须保证的；②反电动势波形为120°平顶梯形，对于方波磁密电机，只要绕组分布均匀且匝数较多时，这点是可以保证的［9］；③忽略齿槽效应和电枢反应等；④磁路不饱和，不计涡流和磁滞损耗。

理想情况下，120°平顶梯形反电动势波形与电流波形如图2所示。

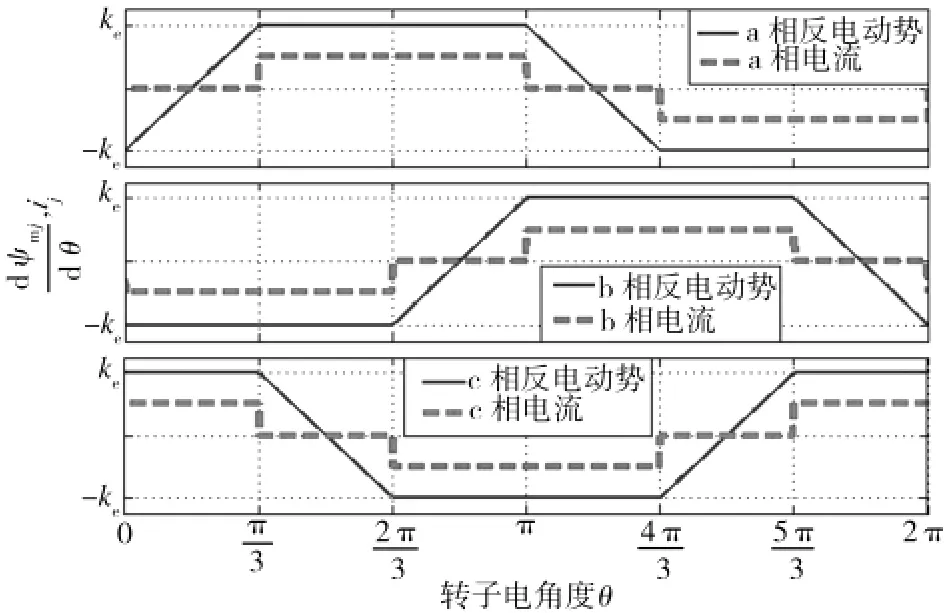
图2 反电动势波形及电流波形Fig.2 Waveforms of Back－EMF and phase current

无刷直流电机系统的等效电路如图3所示。电路工作后，转子转动，控制器通过位置传感器获取电机转子的位置信息。控制器一方面实现换相功能，使电机运转正常；另一方面实现转矩控制功能，一般有两种控制方式，即PAM方式（直接调节输入电压，多用于分析）和PWM方式（调制PWM触发信号，多用于实现），最终使输出转矩跟随目标转矩。

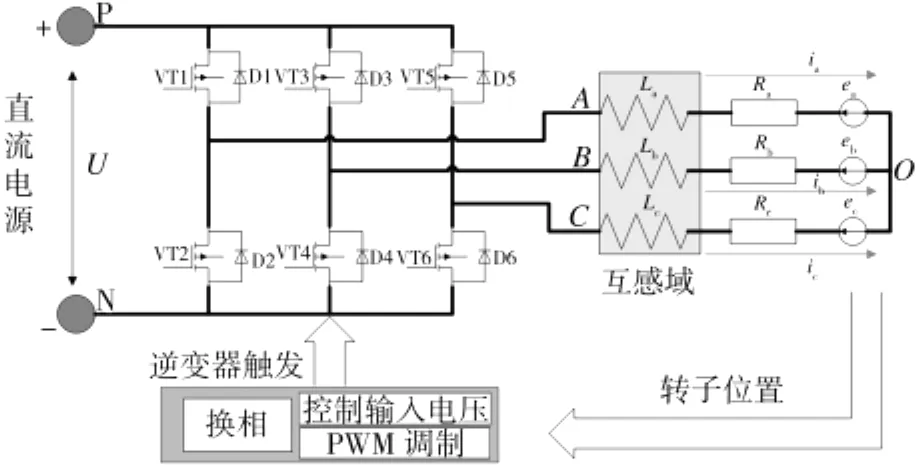
图3 无刷直流电机系统等效电路图Fig.3 Equivalent circuit diagram of BLDCMSystem

由每一相绕组的端电势方程可得到：

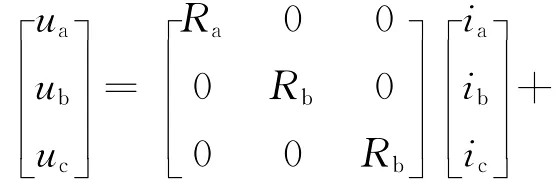
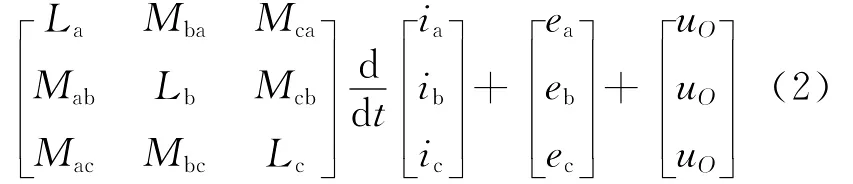
可得到：

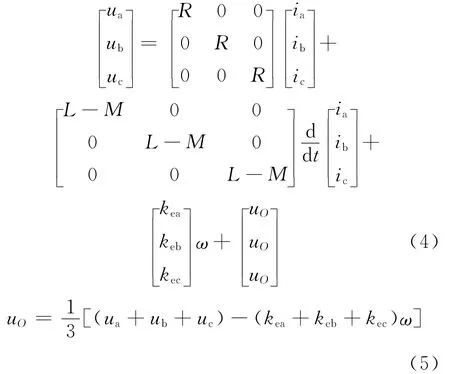
1.2 动力学模型

作为能量转换装置，电机输入为电磁能，输出为机械能。忽略能量转换损耗，由能量守恒定律得：

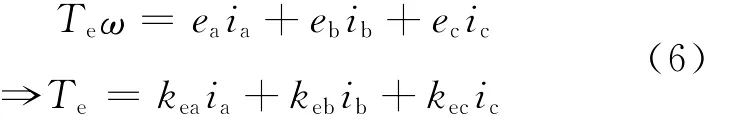
电机的动力学方程为：

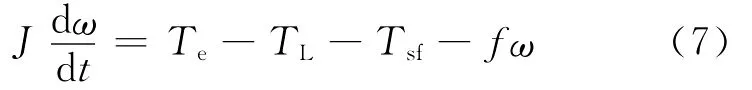
式中：f为阻尼系数；J为转子转动惯量；Te为电磁转矩；TL为负载转矩；Tsf为静摩擦转矩，可按下式计算：

式中：Tsmax为最大静摩擦转矩。

1.3 电机系统模型分析

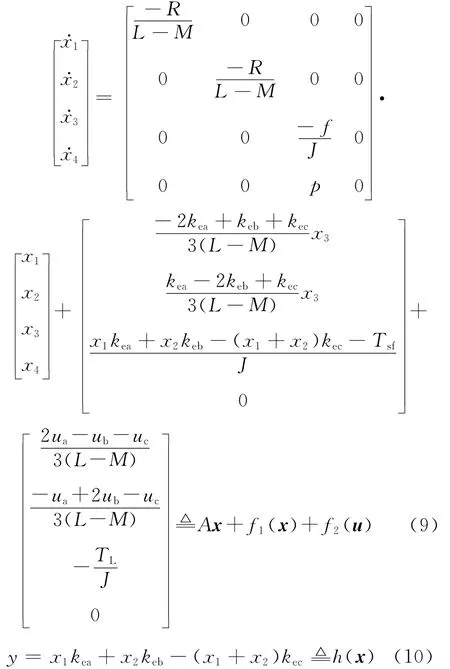
无刷直流电机转矩变化具有阶段性，由于换相期间存在二极管续流，导致转矩波动较大，故续流区间应单独考虑［7］。其特殊性反映在电机系统输入即各相端电势上，续流期间相端电势有突变（见图4），故无刷直流电机具有12个电路工作区间。

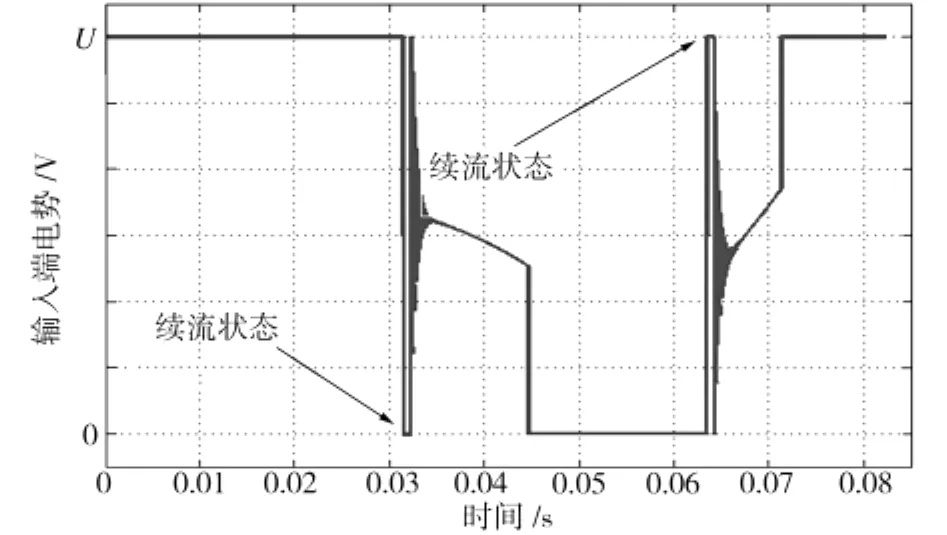
图4 单相绕组端电势一个周期内的仿真图Fig.4 Simulation of single phase terminal voltage in one period

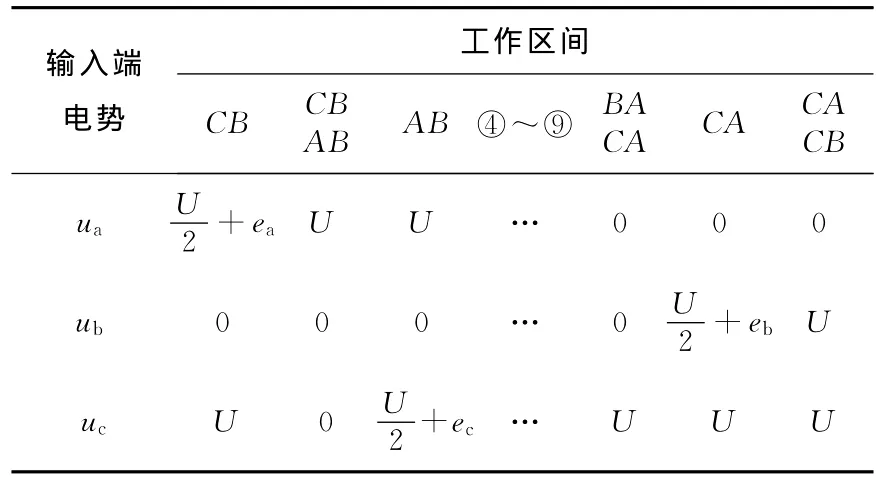
表1 无刷直流电机在12个工作区间的输入端电势Table 1 Terminal voltage of BLDCM during 12 stages

2 基于输入－输出反馈线性化的无刷直流电机控制模型

2.1 控制器数学模型

从输入输出的角度来看，无刷直流电机系统如图5所示，其输入为电源电压，输出为电磁转矩，而负载转矩作为不可控输入。

图5 无刷直流电机输入－输出简化模型Fig.5 Simplified input－output model of BLDCM

假设kea、keb、kec分段可导，则：

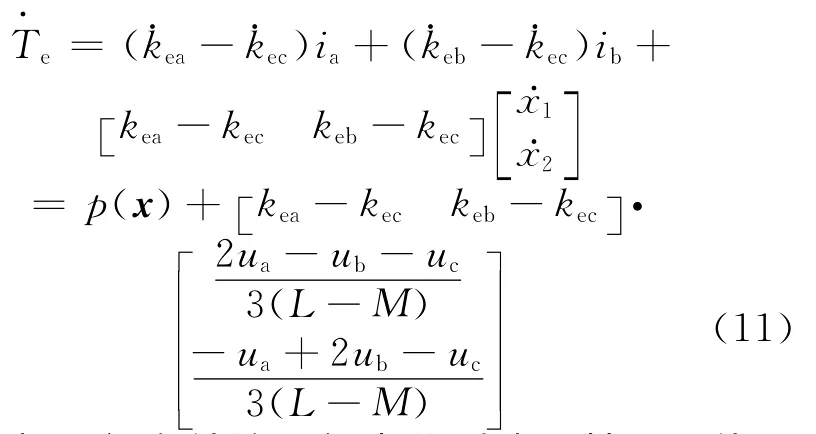
从非换相区间和续流区间中分别选取某一具体区间来讨论。非换相区间以CB区间为例，将各值代入式（11），于是有：

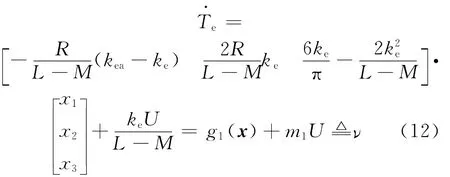
续流区间以CBAB区间为例，将各值代入式（11），同时由于续流持续时间较短，则kec≈ke，于是有：

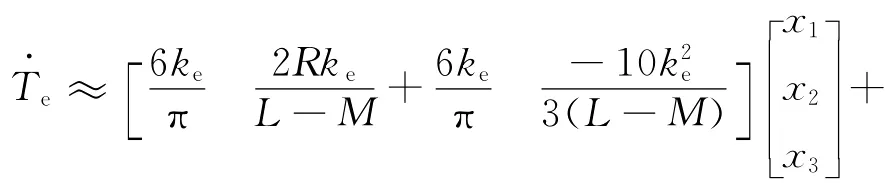
由式（12）和式（13）可看出，系统具有相对阶1。记参考转矩为Tr，取0，记误差e＝Te－Tr则有：

显然，误差e（t）＝e（0）exp（－kpt），e（t）呈指数收敛。只要选取合适的系数kp，系统跟随将快速达到稳定。由式（12）和式（13）反解出，可得到控制器输出。

对其它10种工作区间的分析与上述基本相同，因而可以用一般公式描述对所有工作区间的控制规律。记工作区间i（i＝1，…，12）时参考转矩为控制系数为kp，i，则其实际控制规律如下：

式中：Us为电源电压，为控制器所能提供的最大控制输出。如此，可包括所有区间，同时考虑不同区间的的差异，有进一步优化的可能性。基于输入输出反馈线性化的控制框图如图6所示。

图6 反馈线性化控制方框图Fig.6 Control diagram based on feedback linearization

2.2 内动态分析

由于所研究的控制系统具有相对阶1，而无刷直流电机系统状态量有4个，即便输出稳定，仍需要校验系统的内动态。状态变量中，主要关注的是ia、ib和ω。设ε为足够小的正数，当系统输出趋于稳定时，，即

而kea、keb、kec取值有界，故而状态变量ia、ib有界。由式（7）可知：一般电机负载有界，故ω也有界。

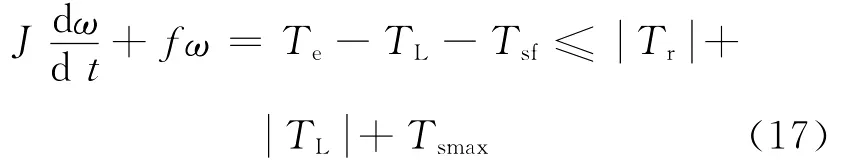
综上所述，采用输入－输出反馈线性化控制策略时，系统内动态是有界稳定的，即对无刷直流电机系统而言，采用反馈线性化控制是一种稳定的策略。

3 基于Matlab／Simulink的控制器仿真验证

3.1 仿真模型的建立

基于Matlab／Simulink仿真平台，采用Stateflow和SimpowerSystem等工具模块的相关函数构建了描述电机相关特性的模型，如图7（a）～（d）所示。

实现公式（15）分区间反馈线性化控制算法的前提条件是准确判定系统所处的工作区间。根据相电流和霍尔位置信号确定系统工作区间：首先，根据霍尔信号确定当前电机所处60°的工作区间；其次，测量相绕组电流，如果其绝对值均大于功率管漏电流，则此时系统处于续流区间，否则处于非换相区间。事实上，由于电机工作时在各工作区间切换顺序固定，采用事件触发方式更容易确定系统工作区间。Simulink中的Stateflow模块提供了事件触发控制的良好平台，本文据此来判定电机所处的工作区间，如图8所示。

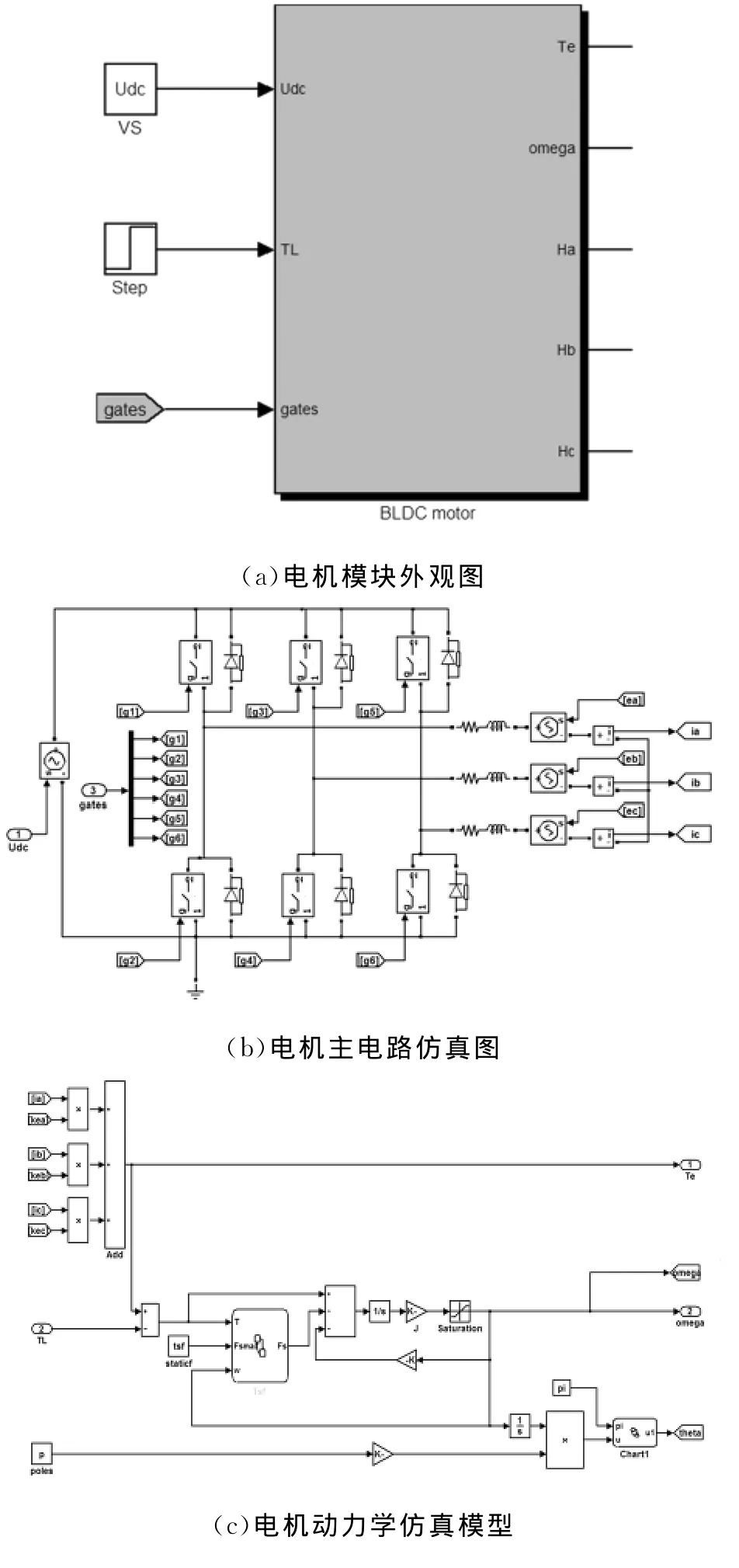
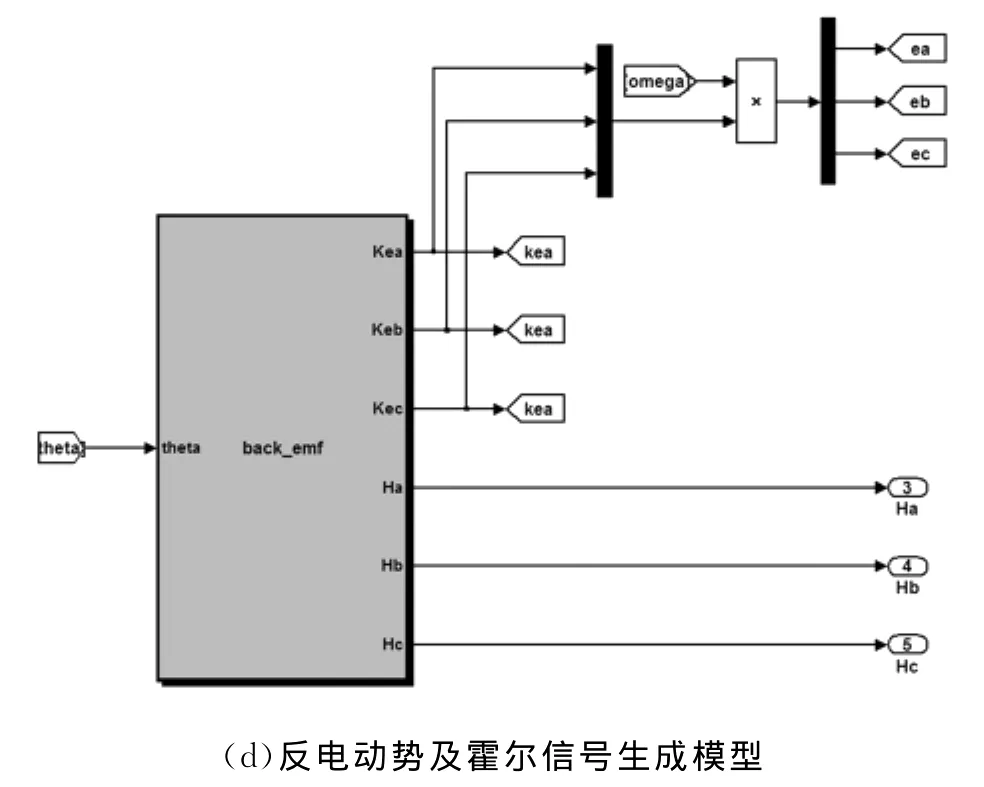
图7 基于Matlab／Simulink的电机仿真模型Fig.7 Simulation model of BLDCM based on Matlab／Simulink

图8 基于Stateflow的电机工作区间判定Fig.8 Stages determination based on Stateflow

加入分区间反馈线性化控制器的无刷直流电机系统仿真如图9（系统PAM仿真）和图10（系统PWM仿真）所示。

3.2 仿真结果与分析

电机参数设置为：电阻R＝0.226 8Ω，自感L＝0.003 8 H，互感M＝－0.001 4 H，阻尼系数f＝0.2 3 8 7 N·m·s／rad，转子转动惯量J＝1.78 kg·m2，反电动势系数ke＝1.62 V·s／rad，极对数p＝1，最大摩擦转矩Tsmax＝30 N·m，电源电压Us＝400 V。跟踪工况设置为：恒转矩区间（Tr＝162 N·m）＋恒功率区间（Pr＝10 k W）；负载转矩阶跃输入（t＝1 s时阶跃输入为30 N·m）。

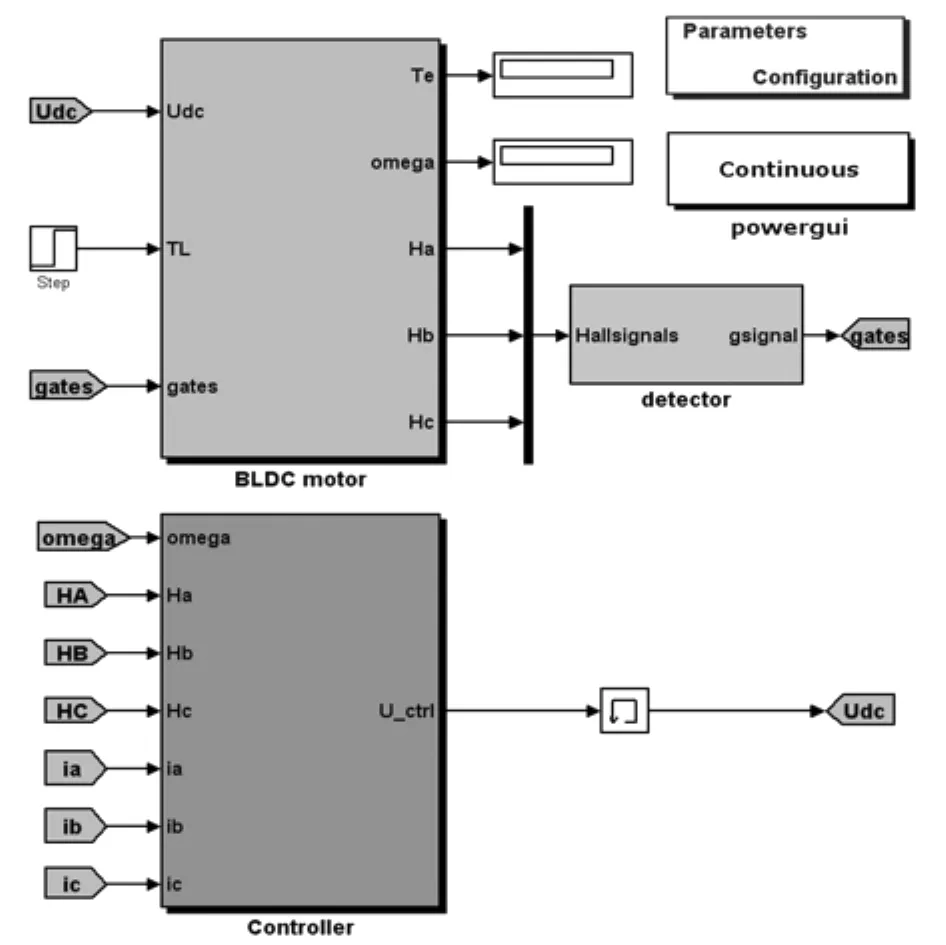
图9 无刷直流电机系统PAM仿真总图Fig.9 PAMSimulation general diagram of BLDCMSystem

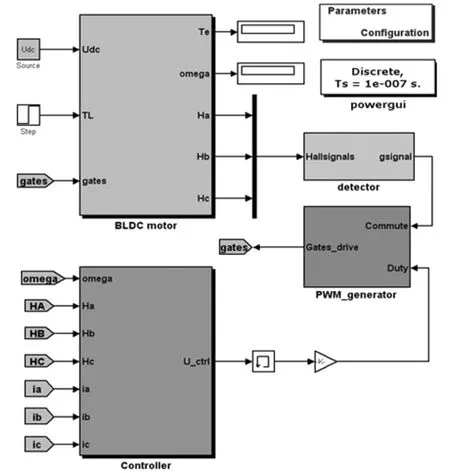
图10 无刷直流电机系统PWM仿真总图Fig.10 PWMSimulation general diagram of BLDCMSystem

3.2.1. PAM仿真

不同于PWM调制所利用的近似效应，PAM直接调节输入电源电压来控制输出，因此更容易针对控制算法本身进行探讨。此时系统等效控制电源电压范围为0～400 V，仿真结果如图11～图13所示。图12中RT为相对误差，用以衡量转矩脉动程度，RT＝（Te－Tr）／Tr。

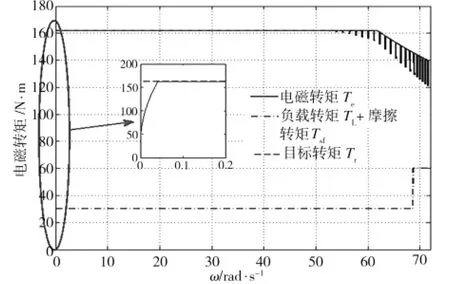
图11 电机转矩跟随效果Fig.11 Torque following effect of BLDCM

图12 反馈线性化控制与PID控制的精度比较Fig.12 Comparison of control accuracy between feedback linearization and PID

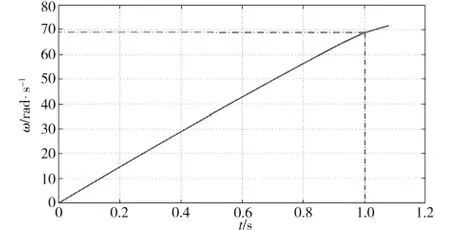
图13 反馈线性化控制下的转子角速度Fig.13 Velocity of the rotator based on feedback linearization control

仿真结果显示，采取反馈线性化控制时，转矩跟随迅速，转速为0.04 rad／s时即跟随上目标转矩；转速在0～50 rad／s区间时，转矩脉动较低，不超过0.01%。对比PID控制，反馈线性化控制响应迅速，且在0～50 rad／s的转速区间内几乎无稳态偏差；t＝1 s时的突加负载对输出转矩影响不大，但对转子角速度有较大影响。这表明低中速时，反馈线性化控制方法对电机转矩脉动抑制及转矩跟随具有良好的效果。然而，当电机转速进一步提高，尤其是转速超过60 rad／s时，转矩脉动抑制效果不佳。

式（15）的控制算法中，控制器实际输出受限，其最大值为车载电源电压。因而当控制器需求电压高于电源电压时，就会出现控制器饱和现象，这直接导致了当转速超过60 rad／s时电机转矩脉动无法有效抑制。控制器需求输出与实际输出的对比如图14所示。事实上，当控制器输出电压不考虑饱和时，电机高速运转时采用反馈线性化方法进行控制，电机转矩脉动也很小，如图15所示。因此，方案中无刷直流电机系统转矩脉动难以完全抑制的原因是车载电源电压有限，控制器输出饱和。

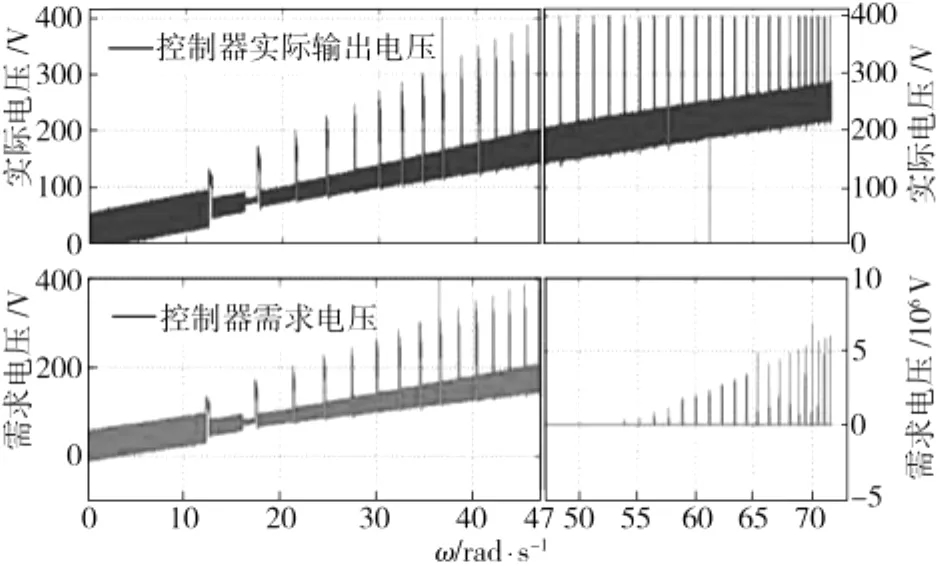
图14 控制器需求输出与真实输出比较Fig.14 Comparison between requested and real outputs of the controller

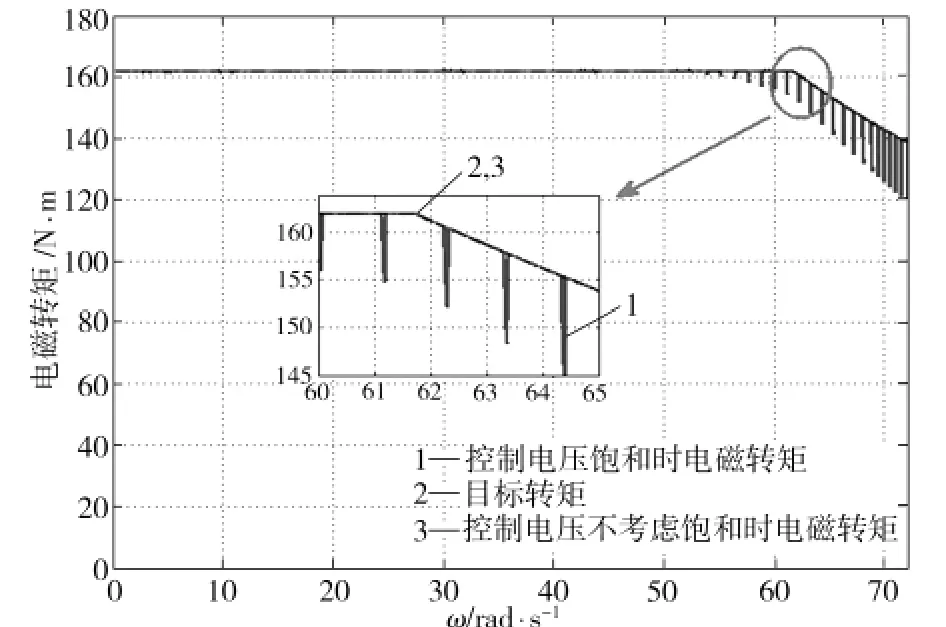
图15 控制电压不考虑饱和时电机转矩跟随效果Fig.15 Torque following effect with unlimited controlled voltage

在采用反馈线性化方法的PAM仿真下，电机效率及相绕组电流如图16和图17所示。

3.2.2 PWM仿真

文中PWM调制采用全桥调制方式，全桥PWM调制时不会出现截止相续流导通的现象［10］，因此该方式在电机的12个工作区间均适用。调制频率为10 k Hz，采用反馈线性化控制，仿真结果如图18～图19所示。

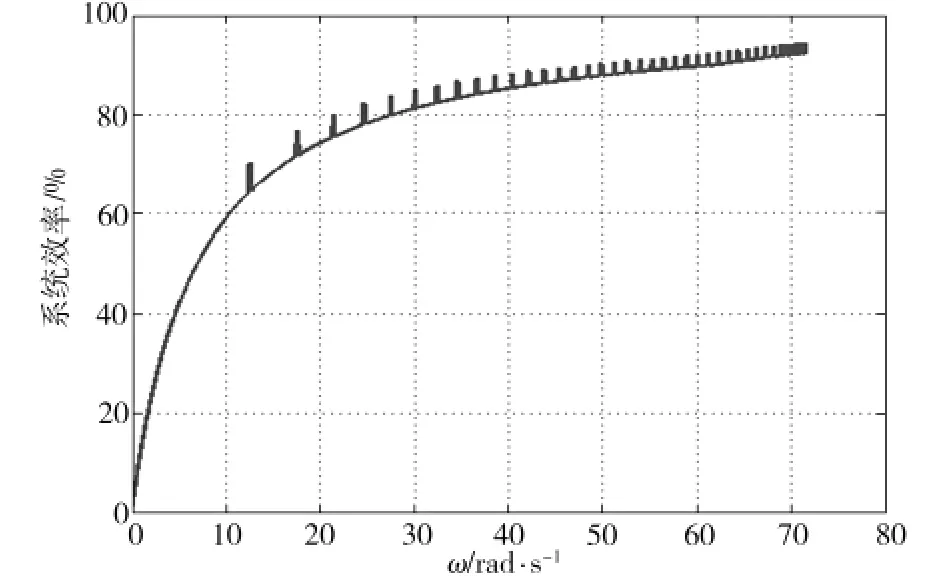
图16 反馈线性化控制下的电机效率Fig.16 Efficiency of BLDCM based on feedback linearization

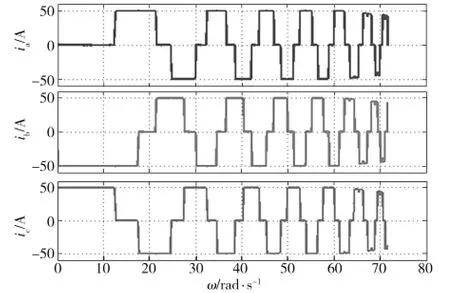
图17 反馈线性化控制下的各相电流Fig.17 Current of three phases based on feedback linearization

由图18～图19可见，PWM仿真结果与PAM仿真结果基本相同。中低速时转矩脉动抑制及转矩跟随效果良好，相对误差有所增大，但仍然控制在0.1%以内。高速时转矩随动效果较好，但转矩脉动增大。

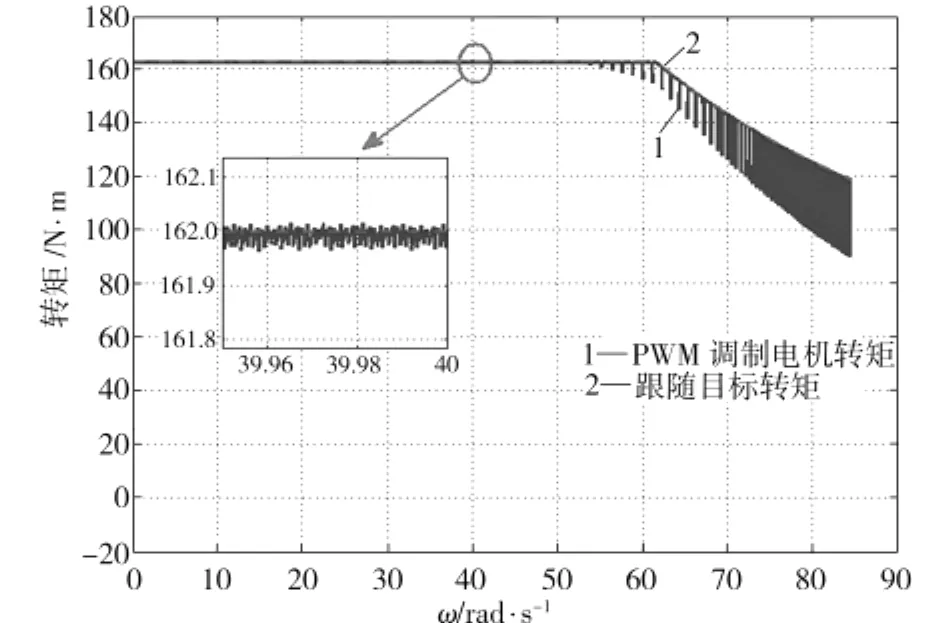
图18 PWM调制下的电机转矩跟随效果Fig.18 Torque following effect of BLDCM by PWM

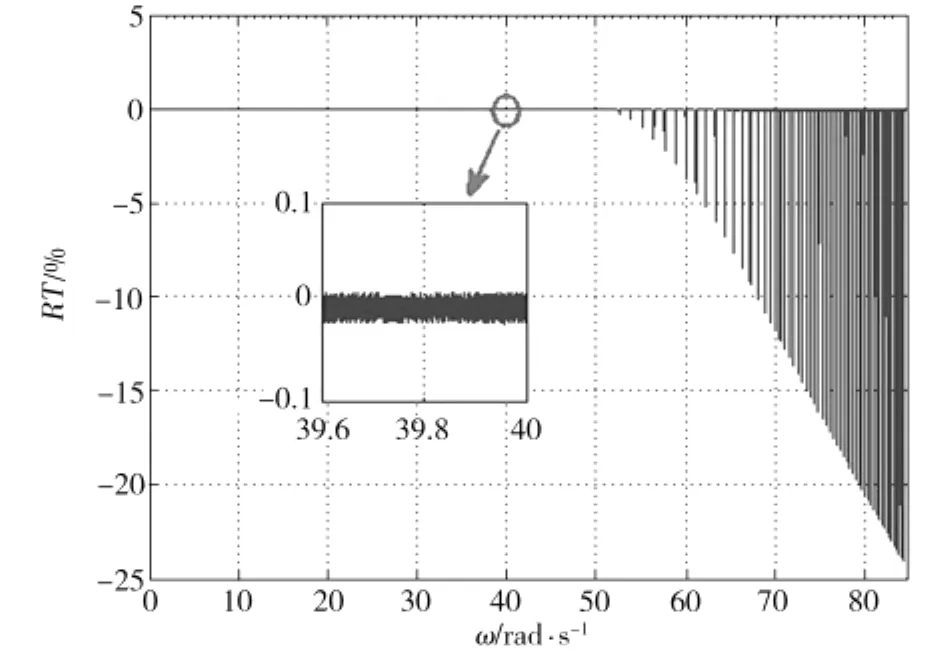
图19 PWM调制下的相对转矩误差Fig.19 Relative tolerance of torque by PWM

4 结语

本文针对无刷直流电机低速转矩脉动抑制及转矩跟随问题，提出了一种基于反馈线性化的解决方案，针对不同工作区间分别进行控制。在起动或低中速工况下，转矩脉动抑制及转矩随动控制效果显著。高速工况下，由于车载电源电压有限，控制器出现饱和特性，导致转矩脉动无法有效抑制。

反馈线性化转矩随动控制算法要求精确确定系统的工作区间及转子转速等，因而提高位置信号及状态变量的获取精度以及控制算法对这些因素的鲁棒性是工程实际中需要解决的问题。

［1］ 贡俊，陆国林.无刷直流电机在工业中的应用和发展［J］.微特电机，2000（5）：15－19.

［2］ 张深.直流无刷电动机原理及应用［M］.北京：机械工业出版社，1999.

［3］ 王宏华.新型交流电动机及控制技术系列讲座（4）永磁无刷电动机控制［J］.机械制造与自动化，2004（4）：18－22.

［4］ 纪志成，沈艳霞，姜建国.基于Matlab无刷直流电机系统仿真建模的新方法［J］.系统仿真学报，2003，15（12）：1 745－1 749.

［5］ 殷云华，郑宾，郑浩鑫.一种基于Matlab的无刷直流电机控制系统建模仿真方法［J］.系统仿真学报，2008，20（2）：293－298.

［6］ Yoshida M，Murai Y，Takada M.Noise reduction by torque ripple suppression in brushless DC motor［C］／／Proceedings of Power Electronics Specialists Conference，1998.PESC 98 Record.29th Annual IEEE，Fukuoka，May 17－22，1998：1 397－1 401.

［7］ 李鲲鹏，胡虔生，黄允凯.计及绕组电感的永磁无刷直流电动机电路模型及其分析［J］.中国电机工程学报，2004，24（1）：76－80.

［8］ Slotine J E，Li Weipin.应用非线性控制［M］.程代展，译.北京：机械工业出版社，2009.

［9］ 武洁，王云艳.集中绕组永磁无刷直流电动机反电动势分析［J］.电机与控制应用，2007，34（7）：6－8，27.

［10］孙立军，孙雷，张春喜，等.无刷直流电机PWM调制方式研究［J］.哈尔滨理工大学学报，2006，11（2）：120－123.