中国财产保险业巨灾损失赔付能力实证分析*

左斐

(西北大学经济管理学院，陕西西安710127)

0 引言

根据民政部2011年1月14日发布的2010年全国自然灾害损失情况，2010全年各类自然灾害共造成约4.3亿人(次)受灾，因灾直接经济损失达5 339.9多亿元。近一年多来，海地、智利、中国台湾、玉树和日本等地接连发生的强震以及甘肃舟曲的特大泥石流等大型灾害事件再次唤醒了人们对超大型巨灾事件的关注，也再次提醒中国加快社会化巨灾风险分散机制的进程。

社会化的巨灾风险分散机制必然要求保险业的参与。尽管巨灾事件所具有低损失频率和高损失幅度的特点使其与经典的可保风险条件相去甚远，一般情况下巨灾风险并不在商业保险的可保风险范围之内。但从实践看，因灾害事件所造成的广泛社会影响，世界上多个与中国类似面临大型自然灾害威胁的国家(地区)在其巨灾保险制度中均赋予商业保险和再保险重要的作用空间。商业保险主动承担和承保巨灾风险已不仅仅是保险业自身拓宽可保风险范围以持续发展的需要，长远来看更是保险业通过承担社会责任履行其特有的社会分工的必然要求。在这样的背景下，对财产保险业所能承受的极限损失幅度和应对极端损失的能力的评估就显得十分必要了。

保险是不确定的经济环境中配置风险的一种经济手段。20世纪中叶，Arrow［1］和Debreu［2］的研究将不确定性正式引入到了传统经济学的分析框架中，证明金融市场可以通过提供有效的金融工具来实现经济中风险的帕累托最优配置，因而即使在不确定性条件下，市场经济也能够实现一般和有效的经济均衡。运用这一框架，Borch［3］考察了保险市场的情形，提出了再保险市场的最优风险分摊规则，说明了不确定性条件下的一般均衡模型是如何用于解决再保险市场中保险人之间的风险分摊问题的。Borch的研究为描述一般均衡框架如何在真实世界中得以实现提供了一个范例，为后来保险经济学理论系统性、规范性研究的形成与繁荣做出了奠基性的贡献。本文对中国财产保险业巨灾损失赔付能力度量所依据Cummins、Doherty和Anita［4］的理论模型就是在Borch的思想和研究框架中发展出来的。

1 中国财产保险业巨灾赔付能力度量模型

Borch的基本结论是，要使保险市场中所有保险人的效用最大化，每个保险人要持有保险市场组合的一个“净份额”，且每个保险人产品的价格取决于其与市场组合的相关度。亦即:在不考虑交易费用的情况下，帕累托最优的风险分担安排“相当于一个联合经营安排，所有的保险公司都把它们的业务汇总到联营公司里来，并同意就联营公司所承担的赔款将如何在各保险公司之间分配定立某些规则”［3］。

Cummins等的保险赔付度量模型正源于这一思想。该模型度量的是单个保险人以及整个财产保险市场对给定巨灾损失的反应能力及反应效率(即赔付能力及效率)。其模型度量方法基于两个基本概念:量(size)与分配(distribution):首先，有多少权益资本或者盈余(surplus)可供分配，其次，保险损失的风险在市场中的保险人之间如何分配(配置)。模型度量的基本前提是:保险市场上负债(保险人预计要付出的保险赔款)配置的目的在于在给定巨灾损失下最大化对保户的赔付。这一基本前提之下，假定单个保险企业自身承担风险有成本而企业之间的风险交易无成本，Cummins等证明了财产保险市场巨灾赔付能力最大化的条件是经再保险分入分出后，每个保险人持有同样的市场保险组合的一个份额，且所有保险人持有的保险组合Li与行业总损失L完全相关，即在所有可能的资源被耗尽，以及运用了所有可能的用以分散和分摊风险的再保险安排后，各个保险人持有份额不同但组成相同的保险组合。这与Borch(1962)的主旨一脉相承。

Cummins等模型中构建了财产保险行业应对巨灾损失的反应函数(Response Function)来代表保险业的赔付能力，这一函数可由图1表示。

图1中横轴表示财险行业总损失的可能值，纵轴表示所有企业预期赔付支出的总和。OZ即为反应函数，它位于45度线上或线下，损失大于期望损失E(L)越多，OZ偏离45度线的距离就越大。这种偏离意味着赔付能力不足的情况随着保险人赔付压力的增大而不成比例地增长。

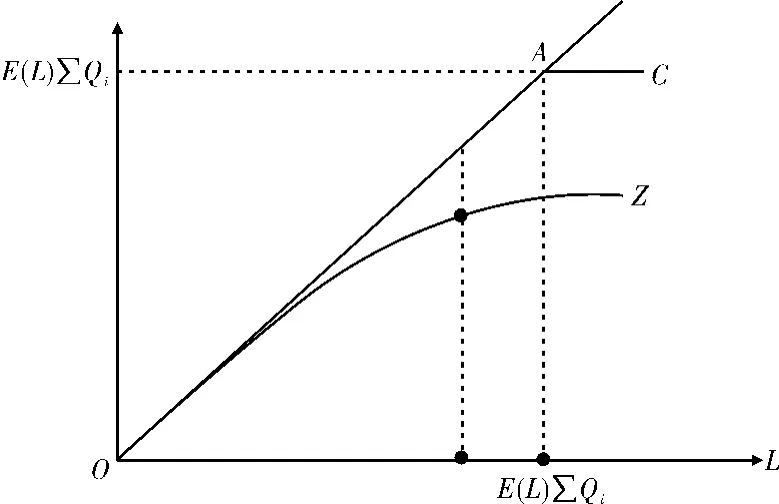
图1 保险业应对巨灾损失的反应函数

假定损失L服从正态分布，根据正态分布的性质，Cummins等经过推导，得到反应函数的表达式为:式中:Pi是保险人i样本区间内净保费(原保费减去再保险分出加再保险摊回)的期望值;Qi0是评估时点上保险人i的权益资本;μi是保险人i样本区间内保险损失(赔付)的均值;σi是标准差;ρi表示单个保险人的损失和总体损失之间的相关系数;Ci=(Pi+Qi0－μLi|L)/σLi|L，μLi|L=μi+ρiσi(L－μL)/σL，σLi|=σi(1－);N(·)是标准正态分布的分布函数;n(·)是标准正态分布的概率密度函数。

损失分布采用更加接近实际的对数正态分布假设后*反应函数变为:其中:

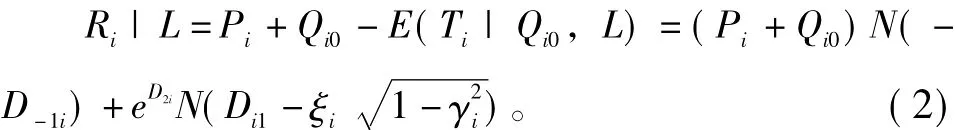
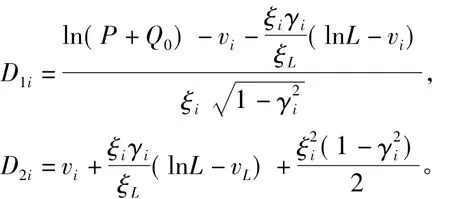
式中:vi和vL是对数正态分布的漂移系数(即对数正态分布的标准差);ξi和ξL是对数正态分布的风险参数(即离差系数，标准差与期望值的比值)。γi是ln(L)和ln(Li)之间的相关系数。通过式(1)和式(2)的比较分析可以看出两式都是随着σi的增加而降低，随ρi的增加而增加。

2 中国财产保险业巨灾赔付能力度量

2.1 样本与数据的选择

根据财险行业应对巨灾损失的反应函数，对财险行业在给定巨灾损失下的赔付能力度量所需要的数据包括:财险公司在评估时点(2009年初)的所有者权益数据，以及在样本区间(1998－2008年)各年的净赔款数额。选择1998－2008年作为样本数据区间的原因如下。

(1)在中国的财产保险行业内，中国人民保险公司每年的赔付额都占相当大的比重(从1998年到2008年依次为80%、80%、80%、78%、75%、73%、69%、57%、42%、46%和43%)，因而对财产保险行业特性的研究必须包含中国人民保险公司，而该公司财险年赔付额数据的记载开始于1998年。

(2)2008年的数次自然灾害对中国财产保险业造成了一定程度的冲击，行业总赔款在上年基础上增加了38.9%，但总保费仅增加了22.5%，行业总资本大约减少了25.2%。因此本文在进行赔付能力的度量中，分别对2008年初和2009年初两个试点上的财产保险业赔付能力进行了度量，一方面旨在发现保险业最近的实际巨灾赔付能力，另一方面也通过对比两个时点考查2008年大灾之年的巨额损失对财产保险业应对极端损失能力的影响程度。

本文度量选取2009年初在中国大陆经营财产保险业务的39家保险公司为样本，并将其分为两类:数据完整的公司(FTS:Full Time Series Company，这类公司1998－2008年各年度的赔款、分保和摊回以及所有者权益数据基本上都有记录)和数据不完全公司(NFTS:Non Full Time Series Company，这类公司在整个研究区间的数据完整度较不理想或者在样本区间初期还没有开始营业，但都可获得2007年或者2008年的相关数据)。在中国财产保险行业中，由于数据资料的不完整，以及部分公司开业时间的限制，度量中的FTS公司的数目共有14家(分别为人保、太平洋财险、平安财险、中华联合、华泰、天安、大众、华安、永安、东京海上、美亚、瑞士丰泰、民安和皇家太阳)，NFTS公司为其余25家，分别为中国信保、三井、三星、永城、安邦、安华、天平、阳光财产、阳光农业、利宝、安盟、都邦、渤海、华农、中银、安联、日本财产、安信、丘博、大地、太平及四家再保险公司中国财产再、慕尼黑再、瑞士再和科隆再。FTS公司的数目虽然不占大多数，但样本区间内其年总赔款和所有者权益均占到了全行业的80%以上，在业务规模和市场影响力方面具有代表性。

2.2 度量过程

对2009年初中国财产保险行业巨灾赔付能力的度量包括以下三个步骤［5］。

第一步，估计FTS公司的原始raw参数和去趋势化影响的detrended参数。估计detrended参数的原因在于:一般来说财险公司的赔付额具有很强的时间趋势，随着时间的推移具有明显的增长趋势，这种趋势是很容易被预测和通过增加保费收入来抵消。因此在评估巨灾和其他类型的随机事件对行业赔付能力的影响时不应当考虑。

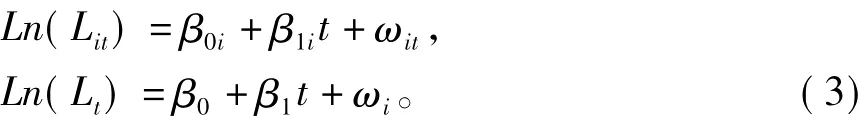
式中:ωit和ωi为回归方程的残差。为了得到去趋势化之后的detrended参数，用上式中ωit和ωi的方差来分别代替σ和σ2。实际引入数据可得14家FTS公司和中国财产保险行业raw参数和detrended参数值。

第二步，将第一步计算中得出的raw参数和detrended参数作为因变量，而其相应公司2008年的多个财务指标作为自变量，代入上面的回归方程中进行参数估计。假设回归模型为多元线性回归模型，作为解释变量的保险公司财务变量包括:①权益资本与资产的比例(E/A);②净损失(净赔款)(LnNL);③权益资本(LnE);④资产回报率(ROA);⑤净收入与净保费的比率(NI/NP);⑥应收分保帐款与总资产的比例(RR/A)。为便于线性模型中系数的估计，净损失、权益资本均取其自然对数值。得到参数估计(略)后将NFTS公司在2008年的赔付额数据代入回归方程中，获得这些公司损失标准差参数的估计值(略)。

第三步，利用上面评估所得出的有关参数的raw值和detrended值，代入反应函数计算39家财险公司在既定巨灾损失下的赔付额，并加总以获得整个财险行业在2009年初的赔付能力。关于巨灾损失的给定，由于2008年中国财产保险行业净赔款为1 210.71亿元，行业权益资本总计515.97亿元，按照模型的规定性，给定巨灾损失的取值范围为从行业总赔款到行业可用于支付赔款的总资源(总赔款与权益的数值和，为1 726.68亿元)，中间每隔100亿元作为一个区间，本文之所以将取值范围超出了总赔款与权益的数值和，是试图发现以及比较中国财产保险行业应对超巨型损失的能力(尤其是像2008年汶川大地震这样的损失)。

3 实证分析结果

使用Matlab 7软件编程计算后得到中国财险行业各公司在2009年初的巨灾赔付能力度量结果，加总处理后得到全行业的度量结果如表1所示。

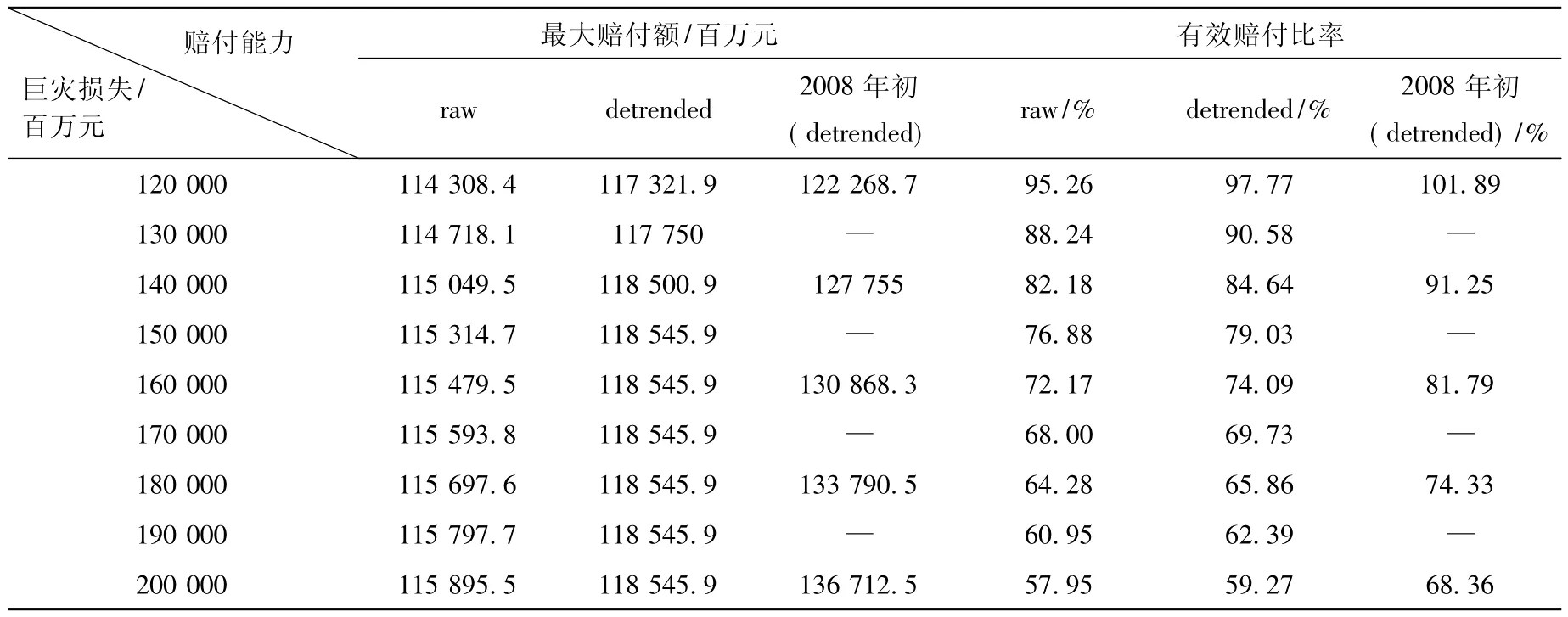
表1 2009年初中国财产保险业巨灾损失最大赔付能力

4 结论

从以上对中国财产保险业巨灾损失赔付能力的度量可得出以下结论:

(1)从去趋势化之后的度量结果看，在1 200亿到2 000亿元的巨灾损失区间内，中国财产保险业的赔付能力缺口在26.8亿到815.6亿元之间，相应的有效赔付比率从97.3%下降到59.3%。赔付能力短缺增加的速度超过了损失增加的速度，表现在1 200亿元之后各个损失区间上，每增加一亿元的损失，赔付能力短缺增加的幅度除在1 300亿到1 400亿元之间出现过小幅降低之外，其他均呈现严格上升态势，尤其在巨灾损失超过1 600亿元之后，短缺增加的幅度和损失增长的幅度持平，表明在现有的行业资本实力条件下，全行业整体的极端损失赔付能力接近其极值。损失对数正态分布假设下行业赔付能力的度量结果更加接近真实水平，据此可推测，即使在更高的财产保险深度水平上(2009年末中国财产保险深度约为0.89%)，对诸如2008年的雨雪冰冻灾害的保险损失(1 500亿元左右)，中国财产保险行业倾其所有也仍然存在20%左右的赔付能力短缺。而对汶川地震这样8 000亿元之上的损失，中国财产保险业只能赔付所有损失中一个极小的比例，这与现实的状况不谋而合。

(2)Cummins、Doherty和Anita的研究显示巨灾损失在2 000亿到5 000亿美元之间时，美国财产保险行业的有效赔付比率介于83.3%到81.6%之间。相比之下，美国的财产保险行业能够以81.6%的比率承受5 000亿美元的损失，而中国的财产保险行业却只能以59.3%的比率承受2 000亿元人民币的损失，中国财产保险业的赔付能力短缺和差距显而易见。造成这种短缺现象的原因，从该度量模型的框架内解释，无疑是由当前全行业资本与盈余的低水平(相比中国财险业2009年初1 726.68亿元人民币的行业资源，美国财险业在1997年的可用资源就达到了3 500亿美元)以及再保险手段应用的不足造成保险损失的风险未在整个行业内达到有效配置所导致的。

(3)本文对2008年初时点上同一损失区间中国财产保险业赔付能力缺口的度量结果在0到632.9亿元之间，相应的有效赔付比率为101.89%到68.36%。与此相比，2009年初时点上的赔付能力缺口的范围扩大，有效赔付比率降低。根据本文前期研究［6］的度量结果，引入与真实损失状况更加接近的损失分布假设后，中国财产保险业(尤其是规模小，风险抵御能力弱的小企业)应对极端损失的赔付能力在一定水平上就出现了停滞的现象。对比2009年初时点上的度量结果，发现在行业现有的资本水平上，财险企业的赔付能力在较低的损失水平上就接近其极值的问题进一步严重，甚至资本实力较强的一些大公司也出现了这样的现象，表明2008年的异常赔付支出进一步降低了财产保险企业本就捉襟见肘的极端损失赔付能力，亦由此可见2008年大灾之年确实对保险业造成了不小的冲击。

(4)中国财产保险业应对巨灾的赔付能力的短缺，再一次强调了政府主动参与巨灾风险分散机制建设并在其中发挥主导作用的必要性和紧迫性。巨灾风险分散机制乃至巨灾保险制度的建设都是复杂的系统工程，但不一定非要等所有细节都明晰之后才开始建设，技术问题、专业问题可由专业人员负责，并在建设过程中不断加以完善，但整体的制度框架亟需尽早启动。近几年，中国在应对巨灾方面已经有了一些前期基础。2007年11月1日施行的《中华人民共和国突发事件应对法》明确规定国家发展保险事业，建立国家财政支持的巨灾风险保险体系，并鼓励单位和公民参加保险;2007年起开始的政策性农业保险试点开展，为建立巨灾保险制度积累了经验;2008年底出台的《抗震救灾法》，进一步明确支持建立巨灾保险制度，并提供相应的财政支持;2009年9月份财政部和税务总局发布了《关于保险公司提取农业巨灾风险准备金企业所得税税前扣除问题的通知》，使长期以来建立巨灾风险准备金可以实行所得税税前扣除的重要问题得以解决，这都为巨灾保险体系建设提供了良好的条件。现阶段需要在已有的法律、政策和市场基础上，由政府统领抓紧启动实质性建设阶段，避免陷入再度发生大型灾害之后中国的整体制度框架仍然处于纸上谈兵的尴尬境地。

［1］Arrow K．Existence of an Equilibrium for a competitive economy［J］．Econometrica，1954，22(3):265－273.

［2］Debreu G．Theory of value:An axiomatic analysis of economic equilibrium［M］．New York:Wiley，1959:98－102．

［3］Borch K．Equilibrium in reinsurance market［J］．Econometrica，1962，30(3):424－446.

［4］Cummins J David，Neil A Doherty，Anita Lo．Can insurers pay for the“Big one”?measuring the capacity of an insurance market to respond to catastrophic losses．［J］．Journal of Banking and Finance，2002(3):557－583.

［5］姚庆海．巨灾损失补偿机制研究——兼论政府和市场在巨灾风险管理中的作用［M］．北京:中国财政经济出版社，2007:449－460．

［6］左斐．中国财产保险业巨灾损失赔付能力实证研究［J］．保险研究，2009(8):65－70．