中国区域定位系统的水平定位误差分布研究*

王 萌，马利华，张丽荣，季海福

(1.中国科学院国家天文台，北京 100012;2.中国科学院研究生院，北京 100049)

中国区域定位系统(Chinese Area Positioning System，CAPS)是基于通信卫星的转发式卫星导航系统。该系统将原子钟放置于地面中心站，导航信号和电文从地面站发射，经由同步通信卫星转发至用户接收机，通过对导航信号的捕获跟踪，接收机实现测距和导航定位。由于系统原子钟放置于地面中心站，CAPS与GPS、GLONASS等直播式卫星系统相比，可以少发射甚至不发射专用导航卫星，可以更容易产生导航电文和易于维护高精度的时间信号。基于这样的设计，CAPS既减少了发射导航卫星的费用又缩短了组建导航系统的周期。在CAPS系统的试验验证阶段，用户接收机通过接收地球静止轨道(Geostationary Earth Orbit，GEO)通信卫星转发的导航信号，结合CAPS气压测高技术实现高程辅助下的导航定位［1－3］。

在卫星导航定位系统中，用户的定位精度主要取决于伪距测量误差和卫星星座的空间布局两个因素。其中，伪距测量误差主要来源于星历误差、卫星钟差、大气传播时延、多路径效应、接收机噪声等;同时，测量误差的大小与信号的强弱和接收机性能有关。星座空间布局一般用精度衰减因子(Dilution of Precision，DOP)描述，其数值可用于估算星座空间布局对用户伪距测量误差的放大程度［4－5］。在相同的伪距测量误差条件下，较小的精度衰减因子值意味着较小的定位误差［5－6］。在试验验证阶段，由于CAPS接收机采用了高程辅助定位方程，这与通常采用的伪距观测方程不同，要分析高程辅助下的定位误差分布特点，需要对现有的精度衰减因子值计算方法进行改造。为了考察CAPS用户的水平定位误差，本项工作中定义了高程辅助定位方程下的东精度衰减因子(Dilution of Precision East，EDOP)和北精度衰减因子(Dilution of Precision North，NDOP)，分析CAPS的仿真和实测数据，并对CAPS用户的定位误差分布特征给了初步的解释。

1 高程辅助下的EDOP和NDOP计算

通常情况下，在地心地固坐标系中用户的伪距观测方程可写为:

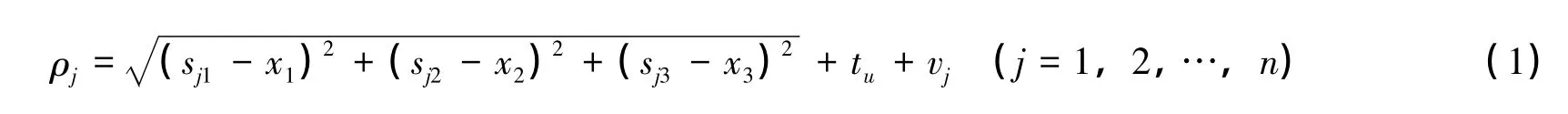
式中，ρj为伪距观测值;(sj1，sj2，sj3)表示卫星sj的三维坐标;(x1，x2，x3)表示用户的三维坐标;tu表示用户的时钟偏差;vj表示伪距测量误差。将(1)式按泰勒级数在用户近似位置展开:

式中，δρj表示真实伪距与估计伪距的差值;δxi(i=1，2，3)表示对用户近似位置的修正量。上式的矩阵形式为:

这里，系数矩阵H中(ej1，ej2，ej3)对应用户到第j颗卫星的方向余弦;v是伪距测量的误差向量。利用最小二乘法，定位解可由下式给出:

这里，HT是矩阵H的转置矩阵。据此，可以求解用户的三维坐标和接收机钟差。

为了更直观地描述用户的位置信息，将(3)式中的系数矩阵转换到站心坐标系内，转换矩阵为:

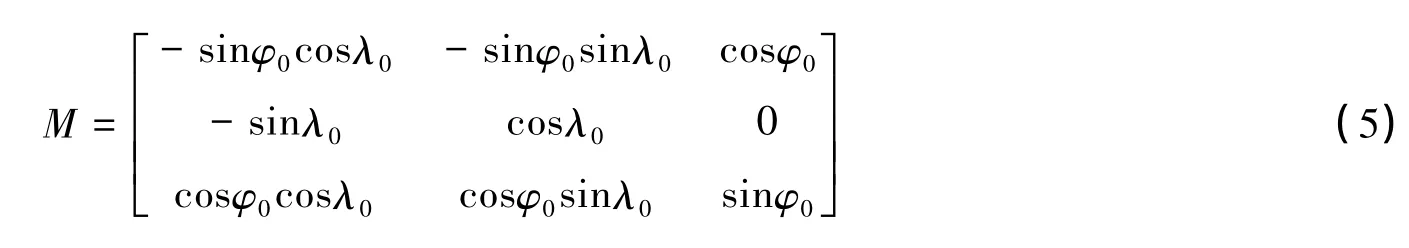
式中，φ0和λ0分别为测站的大地纬度和大地经度。引入精度衰减矩阵Q=(HTH)－1，矩阵Q的分量形式可表述为:

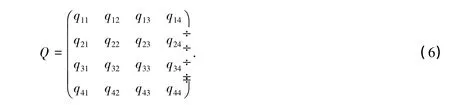
几何精度衰减因子(Geometric Dilution of Precision，GDOP)由下式给出:

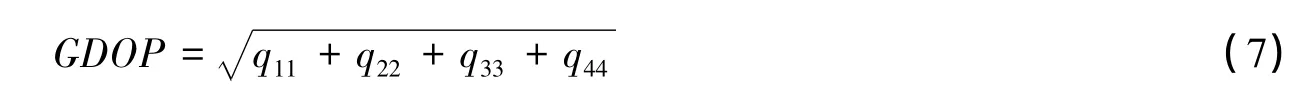
常规精度衰减因子还包含三维位置精度衰减因子(Position Dilution of Precision，PDOP)、水平精度衰减因子(Horizontal Dilution of Precision，HDOP)、垂直精度衰减因子(Vertical Dilution of Precision，VDOP)和时间精度衰减因子(Time Dilution of Precision，TDOP)，它们分别可利用下式计算:

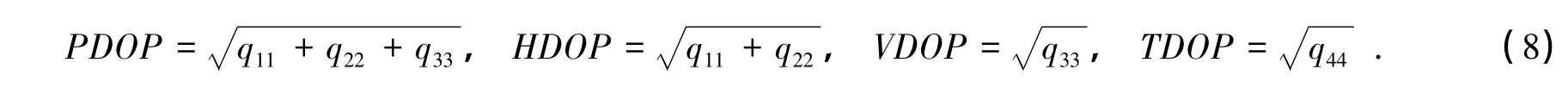
式中，HDOP和VDOP分别描述了星座布局对伪距测量误差在水平和垂直两个方向上的误差放大程度，因此，HDOP和VDOP只有在站心坐标系下计算才有意义。

在CAPS试验验证阶段，用户接收机利用气压测高计获取本地高度，仅用3颗卫星就可以实现用户的三维定位。当然，更多的可视卫星可以进一步改善用户的定位结果。在CAPS高程辅助定位算法中，气压测高计测量的高度值被转换为用户到位于地球中心的虚拟卫星的几何距离［7］。CAPS气压测高的精度优于2 m，通过合理布局气象基准站，可以得到更高的测高精度［3，8］。由于气压测高的伪距观测方程不受用户接收机的时钟偏差的影响，CAPS接收机伪距观测方程和气压测高观测方程的泰勒展开公式为:

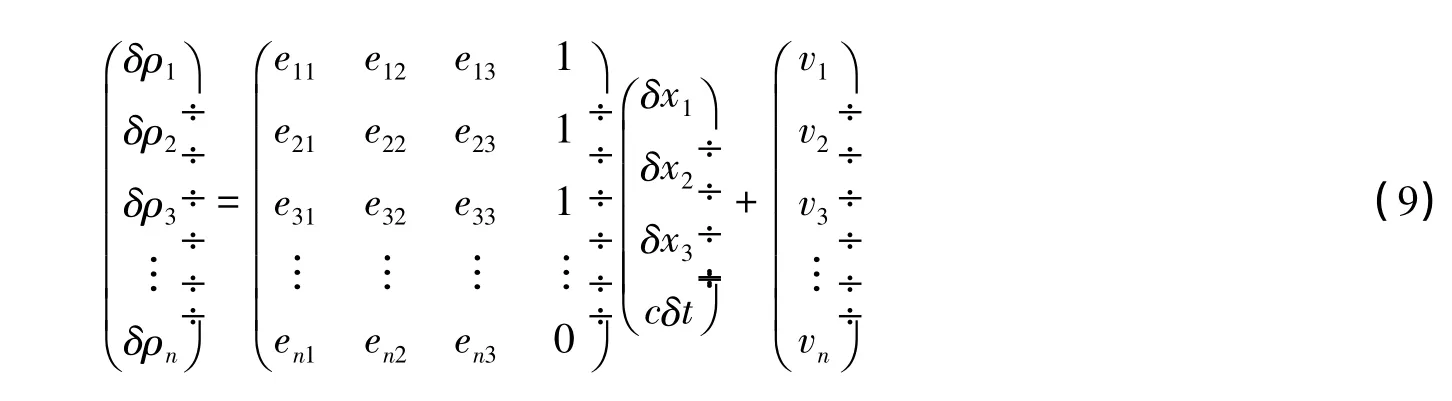
式中，δρk(k=1，2，3，…，n)表示基于真实高度转换的伪距与基于估计高度转换的伪距的差值;vn表示高程测量的误差。由于用户接收机本地高度值是由高度计提供的，在站心坐标系下计算精度衰减矩阵Q时，不再考虑高程方向。此时，Q是一个3×3矩阵，其分量形式如下:

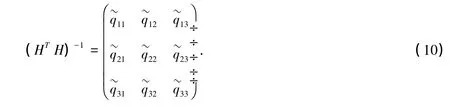
2 分析与比较

2.1 EDOP和NDOP覆盖

CAPS试验验证阶段的3颗GEO通信卫星分别位于87.5°E、110.5°E和142°E轨位。根据上文对EDOP和NDOP的定义，可以计算出系统星座覆盖区内任一地点的EDOP和NDOP值(图1)。

由图1可见，赤道面附近的条带区域是该系统星座的盲区，这是由于当用户接近赤道面附近时，(10)式中EDOP和NDOP不存在。从图中还可以看出，EDOP和NDOP是南北对称分布的，这是由于GEO通信卫星位于赤道面附近，所以北半球和南半球的EDOP和NDOP分布关于赤道面对称;同时还可以注意到，两个因子也是东西对称分布的，这种分布特征主要源于系统采用GEO卫星的轨位分布。在覆盖区域内，EDOP数值在1.3到7.9之间变化。EDOP最小值出现在3颗GEO卫星定点轨位的平均经度子午圈附近;在同一纬度圈上，离该子午圈越远，EDOP数值越大。总体而言，任一格点上的NDOP总是大于EDOP，NDOP最小值为9.2，最大值达到80甚至更大，这是由于系统采用的卫星都处于赤道面附近，东西方向拉开，而南北方向比较集中。当用户由低纬度地区向高纬度地区移动时，在站心坐标系内卫星在南北方向拉开的距离增大，NDOP变小。

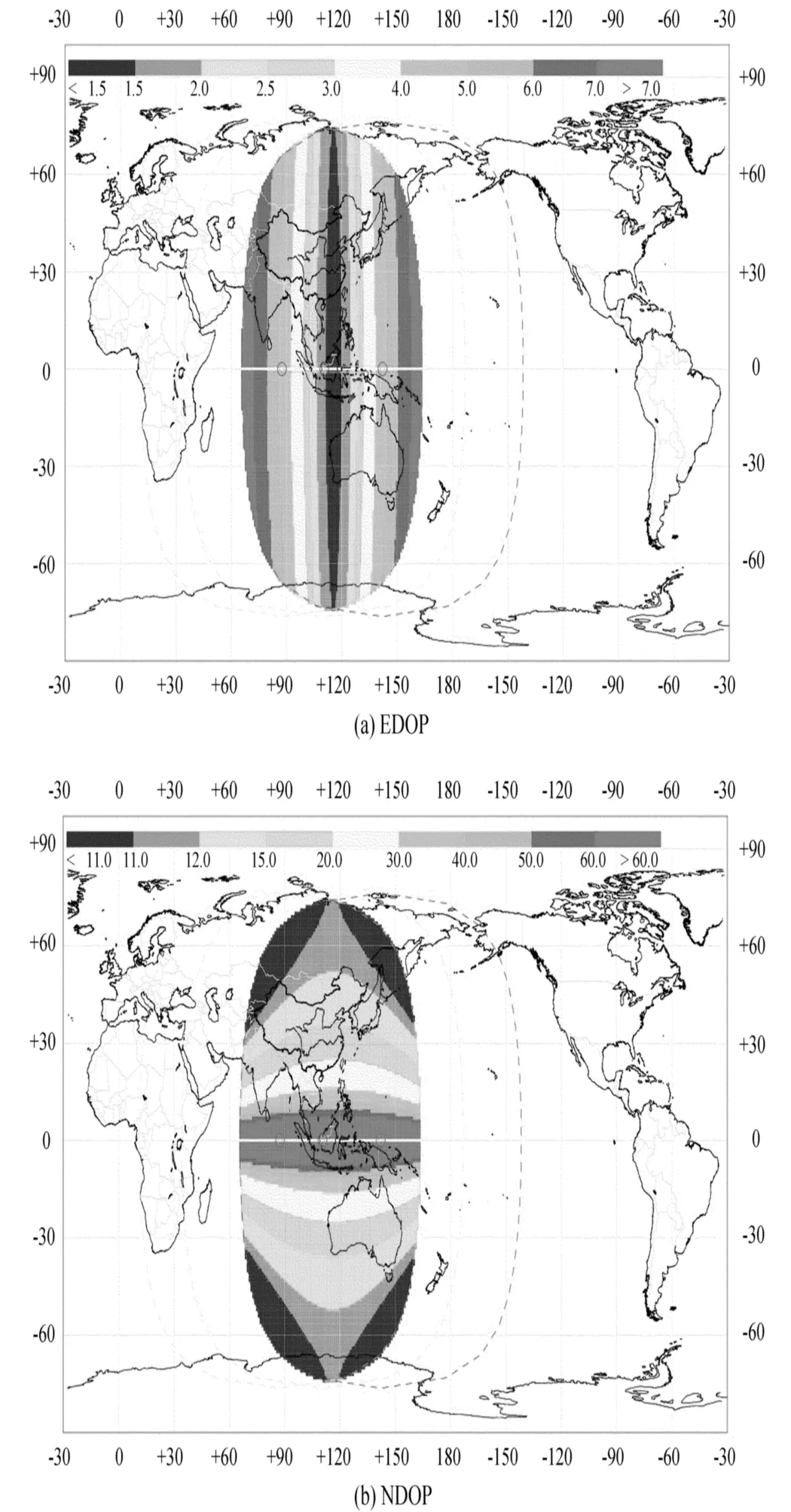
图1 CAPS试验验证星座的EDOP(a)和NDOP(b)覆盖图Fig.1 Coverage maps of EDOP(a)and NDOP(b)for the satellite constellation during the test stage of CAPS

2.2 仿真分析

如前节所述，EDOP小于NDOP，因此东西方向的定位精度总是优于南北方向。为了验证这一点，分别选择北京、上海、长春、西安、乌鲁木齐和昆明观测站位置作为用户接收机位置进行仿真，3颗卫星分别位于87.5°E、110.5°E和142°E同步卫星轨位，在每一测站生成3600 s(步长1 s)的仿真数据，给定的伪距测量误差服从均值为0，均方根(Standard Deviation，STD)为0.5 m的正态分布。根据上述仿真参数设置，可以求得高程辅助下的定位结果，这些地点的水平定位误差分布绘于图2。

由图2可见，6个台站的水平定位误差呈椭圆分布，东西方向的定位精度总是优于南北方向，这与图1的结论是一致的。根据EDOP和NDOP的定义，东西方向和南北方向的定位误差的均方根(STD)除以伪距测量误差(0.5 m)，即对应于东西方向和南北方向的误差放大倍数。在表1中，同时计算了EDOP和NDOP的理论数值与仿真结果进行了比较。

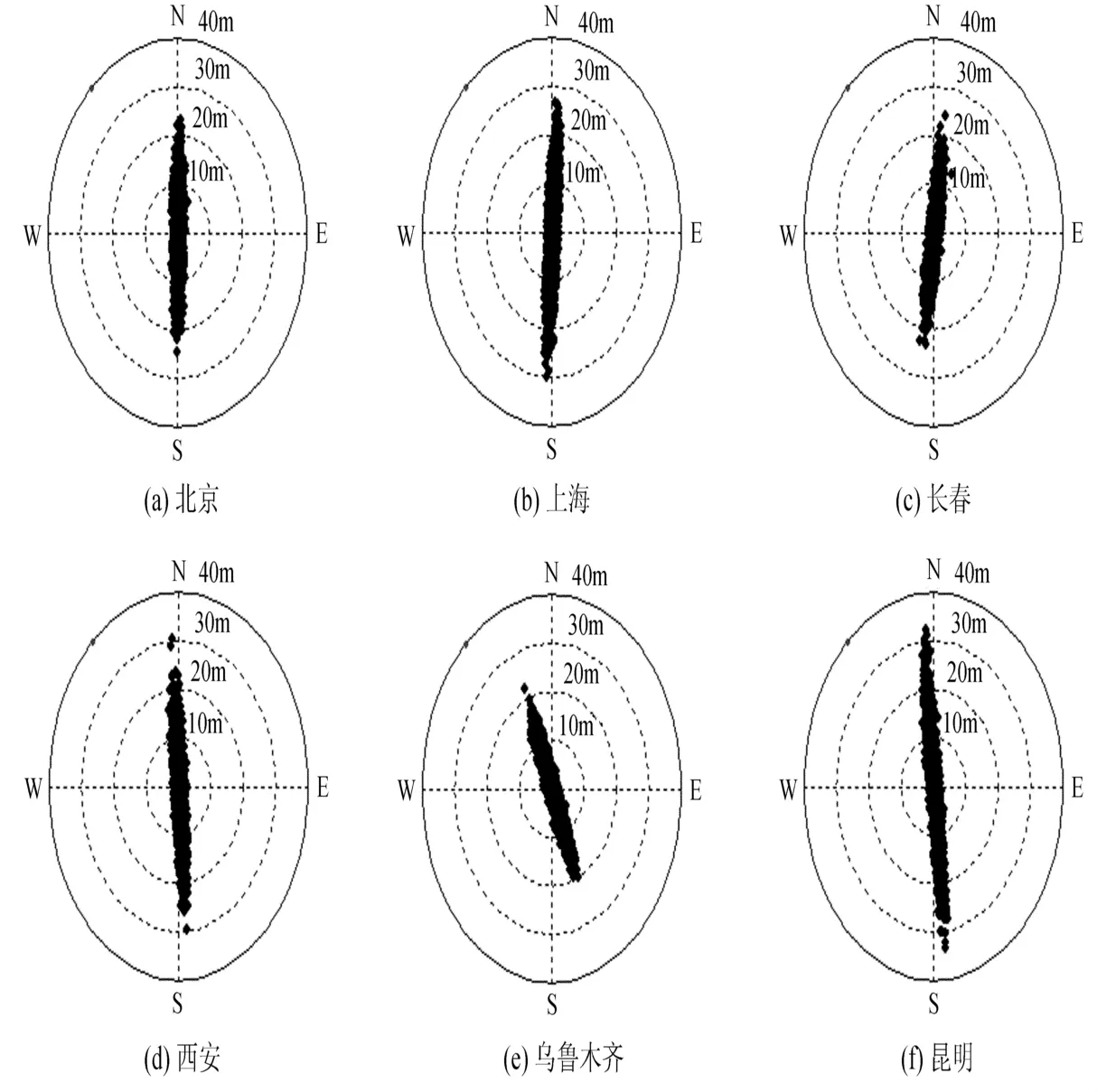
图2 利用仿真数据得到的测站水平定位误差分布Fig.2 Error distributions of horizontal positioning of various ground stations based on simulations of the CAPS test

从表1可以看出，EDOP和NDOP计算的理论值与仿真结果基本一致，说明可以用本文定义的EDOP和NDOP描述东西方向和南北方向的误差放大倍数，再乘以伪距测量误差可以得到这两个方向上的定位精度。

2.3 实测数据分析

事实上，在CAPS试验验证阶段，6台测试用接收机已被安置在上述6个台站，并实时采集测量数据。实测数据采集时间为2005年6月30日16:10到17:10，时间间隔为1 s。考虑到测试期间，该时间段内卫星无机动，卫星的轨道误差很小;电离层效应、对流层效应则主要影响到定位偏差，在接收机内部没有改正这些偏差。在分析实测数据时，为了清晰地展示定位误差的椭圆分布特征，在定位结果中去掉定位偏差。图3给出上述6个台站在水平面内的定位误差分布。

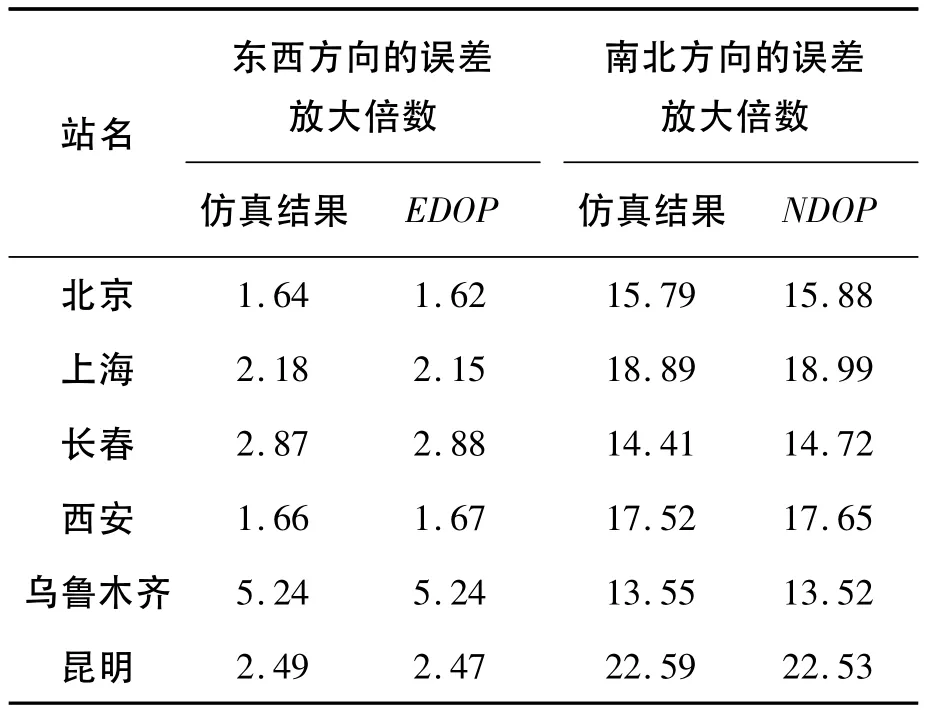
表1 仿真数据得到的误差放大倍数和EDOP/NDOP理论比较Table 1 Comparison between simulated and theoretical error amplication factors for EDOP and NDOP

这里，利用实测数据也得到与仿真数据类似的误差分布特征:6个台站的定位误差分布存在明显的水平椭圆误差分布，南北方向误差大于东西方向误差，定位误差椭圆的半长轴与本地的南北方向夹角也与仿真结果相似。图3中用户在水平面内的定位误差主要来源于接收机的测量噪声。

为了便于和仿真数据做比较，计算了实测数据中南北方向和东西方向的定位误差放大倍数的比值，结果列于表2。其中，第2列是利用表1中第5列除以第3列得到;第3列是利用表1中第4列除以第2列得到。

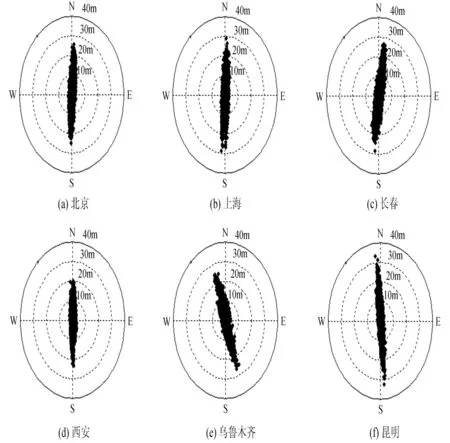
图3 利用实测数据得到的测站水平定位误差分布Fig.3 Error distribution of horizontal positioning of various ground stations based on observational data

由表2可以看出，由仿真数据得到的南北方向定位误差与东西方向定位误差的比值与理论计算的NDOP与EDOP的比值非常一致。由实测数据得到的南北方向定位与东西方向定位误差比值与理论计算的NDOP与EDOP的比值比较接近，接近程度因测站不同有所差异。由于不同测站观测GEO卫星的高度角不同，造成传播路径时延的复杂性和实测数据的复杂特征，从而导致在实测结果与仿真结果之间存在一定差异。仿真分析中，系统星座由同步轨道GEO卫星组成，卫星处于理想的赤道面内;在实测中，由于受到日月等摄动力的作用，GEO卫星并不严格处在赤道面上，因此，表2和表1中的NDOP/EDOP略有差别。

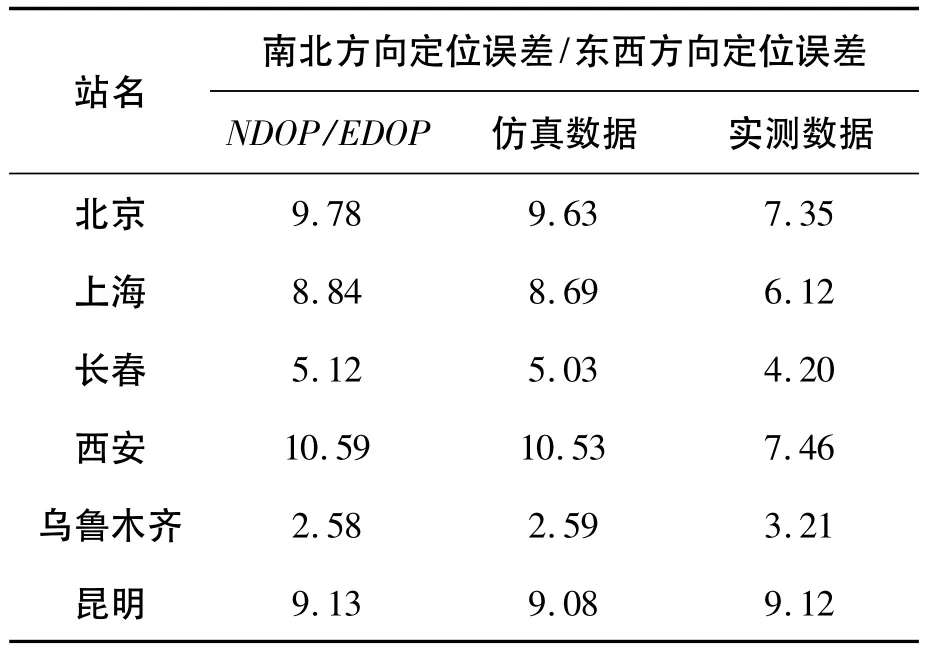
表2 南北方向定位误差和东西方向定位误差的比值Table 2 Ratios of NDOP/EDOP from theoretical calculations simulation and observations

3 结语

本文给出了高程辅助下的EDOP和NDOP的计算方法，该计算方法在计算精度衰减矩阵时，只考虑东西方向、南北方向和钟差，不再考虑高程方向。通过对CAPS覆盖范围内高程辅助定位算法下EDOP和NDOP的计算表明，本文定义的EDOP和NDOP可以很好地解释CAPS用户接收机在高程辅助下水平定位精度东西方向总是优于南北方向的原因。通过对北京、上海、长春、西安、乌鲁木齐和昆明6个测站仿真和实测数据分析表明，这两个因子可以被用来描述东西方向和南北方向的误差放大倍数，可以用来估算两个方向上的定位精度，进而估算水平定位精度。

致谢:文中所用实测数据来源于CAPS临潼导航主控站，在此表示感谢。

［1］艾国祥，施浒立，吴海涛，等.基于通信卫星的定位系统原理 ［J］.中国科学 (G辑):物理学 力学 天文学，2008，38(12):1615－1633.

［2］Ai Guoxiang，Shi Huli，Wu Haitao，et al.A positioning system based on communication satellites and the Chinese area positioning system(CAPS) ［J］.Chinese Journal of Astronomy and Astrophysics，2008，8(6):611－630.

［3］Ai Guoxiang，Sheng Peixuan，Du Jinlin，et al.Barometric altimetry system as virtual constellation applied in CAPS ［J］.Science in China Series G:Physics Mechanics and Astronomy，2009，52(3):376－383.

［4］Han Yanben，Ma Lihua，Qiao Qiyuan，et al.Selection of satellite constellation framework of CAPS［J］.Science in China Series G:Physics Mechanics and Astronomy，2009，52(3):458－471.

［5］Kaplan E D，Hegarty C J.Understanding GPS:principle and application ［M］.Boston:Artech House，2006.

［6］谢钢.GPS定位原理与接收机设计 ［M］.北京:电子工业出版社，2009.

［7］张丽荣.CAPS广域差分方法研究 ［D］.北京:中国科学院研究生院，2008.

［8］张丽荣，马利华，王晓岚.CAPS气压测高的仿真分析［J］.微计算机信息，2011，27(3):185－186.Zhang Lirong，Ma Lihua，Wang Xiaolan.Simulation analysis of CAPS barometric altimetry ［J］.Microcomputer Information，2011，27(3):185－186.