基于Jurkevich法Cyg X-1光变周期特性研究*

董爱军

(滁州学院机电学院，安徽 滁州 239000)

通过功率谱分析，人们发现黑洞候选体X射线双星Cyg X-1存在420 d和150 d的光变周期［1］。虽然功率谱分析法是当前处理天体光变周期行之有效的方法之一，但是，由于该方法只能处理等时间间隔的观测数据，分析天体的光变周期往往需要进行插值或曲线拟合，这必然带来一些不真实的信息，增加了光变周期准确性认证的困难。Jurkevich法［2］是一种建立在期望值均方误差基础上的频谱分析方法，该方法最大的优点是能够直接处理非等时间间隔的观测数据，真实反应天体光变曲线的周期特征［3－4］，而且利用该方法已经成功讨论了许多天体的光变周期［5－12］。另外，Kidger等［1，3］引入的表征周期特性可信度的Kidger判据，扩大了Jurkevich法的适用范围。

为了讨论黑洞候选体X射线双星Cyg X-1的光变周期，本文利用Jurkevich法和Kidger判据，分析了黑洞候选体X射线双星Cyg X-1近16年Rossi X-ray Timing Explorer(RXTE)All-Sky Monitor(ASM)观测资料。本文第1节给出数据处理方法，第2节给出分析结果，第3节对结果进行了讨论，文章的最后给出了本文的结论。

1 数据处理

1.1 Jurkevich 法

Jurkevich法［2］是一种基于期望值均方误差的统计方法，它把观测数据按试验周期折叠，分为m组，并对每组求均方误差，然后取总方差。若试验周期等于实际周期，则出现最小值［2，4］。

对于某段光变曲线{xi，i=1，2，3，…，N}，利用Jurkevich法分析其光变周期主要包括以下几个步骤:

(1)根据试验周期p把光变曲线{xi，i=1，2，3，…，N}分成m组

给定观测点进入的分组索引号为:

式中，char是取整运算;p为试验周期;t0为观测数据起始时间。则组索引号的取值范围NDGR={0，1，2，…，m－1}。

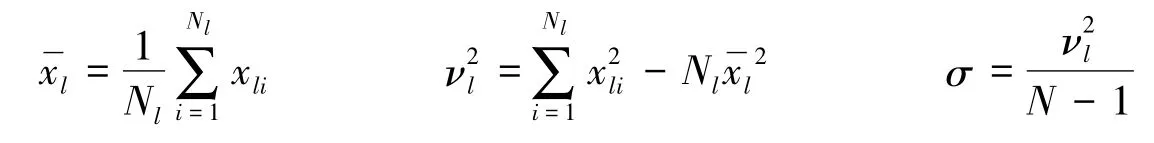
则m组的总方差:

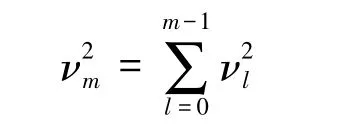
(3)归一化

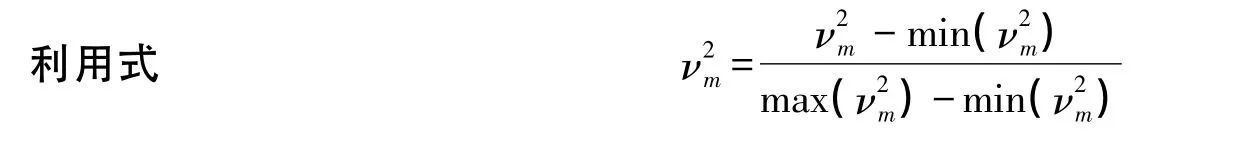
由(1)和(2)步可知若光变曲线{xi，i=1，2，3，…，N}存在某一光变周期T，则在p－图上，p=T处，应出现最小值。

(5)误差分析

本文取峰值的半最大值半宽度(Half Width at Half Maxium，HWHM)作为对应光变周期的误差范围。

1.2 Kidger判据

1992年Kidger给出了 Jurkevich法判别p－图中光变周期真伪性的 Kidger判据［13］:若为归一化的，则

f≥0.5:光变曲线存在很强的周期特性; f≤0.25:光变曲线存在较弱的周期特性;f=0:光变曲线不存在周期特性。

1.3 分组m及观测时间跨度对观测结果的影响

在计算过程中，m的选择十分重要，m越大灵敏度越高，但会产生越大的噪音;m太小则找不到相应的光变周期［2］。同时，观测时间跨度对光变周期的确定影响也十分大，一般情况下，观测时间跨度要大于6倍有效周期［13］，但是如果数据分布较好，1.5个周期的观测时间跨度就可以了［4，14］。

2 结果与分析

利用Jurkevich法分析处理了黑洞候选体X射线双星 Cyg X-1 MJD=50087－55841期间的ASM观测资料，结果表明，Cyg X-1存在明显的光变周期特性。利用Jurkevich法分析光变曲线的周期特性时，分组数m的选择通常会影响光变周期特性的认证。为了准确测定Cyg X-1的光变周期，本文取m=(10，15，20)，试验周期p从1 d到1200 d，步长为1 d。

图1给出了Cyg X-1 MJD=50087－55841期间软X射线波段的光变曲线以及硬度比(Hardness Ratio，HR)的时变特性。从图中可以看出，Cyg X-1光子计数率变化十分剧烈，经历了数次态的转换，但光变周期特性并不显著。传统上，一般采用功率谱法和相位分析法等手段分析其光变曲线的特征频率。这些方法处理具有固定步长的离散观测数据的光变周期较为方便，但对于非均匀采样的观测数据，往往需要通过插值法或曲线拟合，这必然带来一些不真实的信息，增加了光变周期准确性的认证困难。利用Jurkevich法很好地解决了这些问题。图2给出了不同m时，试验周期p与总方差的关系曲线。从图中可以看出，总是在某些试验周期处出现最小值。

图1 1996年1月至2011年10月黑洞候选体X射线双星1.5－12 KeV能段上，Cyg X-1的光变曲线以及对应的硬度比HR。上图:光变曲线，下图:硬度比HRFig.1 The Light Curve and Hardness Ratios of the black-hole candidate X-ray binary Cyg X-1 from January 1996 to October 2011 in the 1.5－12KeV energy band

从图2和表1可以看出，在m=(10，15，20)3种情况下，黑洞候选体X射线双星Cyg X-1的光变曲线都存在363±11.5 d的光变周期。同时，在试验周期为728±24 d和1120±42 d时，也出现极小值，而且周期特性十分明显(f＞0.5)。由于该周期近似为363±11.5 d的倍数关系，因此可能是363±11.5 d周期的观测表象。另外，从图2和表1还可以发现，Cyg X-1存在51±1.4 d的光变周期，其Kidger判据0.25≤f≤0.5，同时还发现了该光变周期的倍数周期(102±0.9 d、153±0.9 d以及314±5 d)。

表1 不同m值，试验周期p对应的Kidger判据fTable 1 The trial period p and the Kidger f for different values of m

图2 m=(10，15，20)时，试验周期步长为1 d的p－曲线Fig.2 The p－curves for m=(10，15，20)and step of tiral period=1 day

3 讨论

文［1］作者利用1996～2001年Cyg X-1处于硬态时的ASM和PCA资料，计算分析了该天体光变曲线的功率密度谱，发现Cyg X-1存在p=150 d和420 d的光变周期(图3)。通过对不同波段功率密度谱分析，他们认为150 d的光变周期只是光度变化的一种反映，而420 d的光变周期是软X射线流的内在反映，同时影响着X射线谱的变化。但是功率密度谱通常只能处理固定时间步长的观测数据，在处理不等时间步长的观测数据时，往往需要进行插值或曲线拟合，这必然会影响信息的真实性。Jurkevich法是一种建立在期望值均方误差基础上，能够处理非等时间间隔数据的频谱分析方法，能够充分反映观测数据的真实性。

Kidger［13］指出，利用Jurkevich法计算光变曲线的周期特性时，数据的最小时间跨度为6倍有效周期长，图2给出的51±1.4 d和363±11.5 d的光变周期满足这个条件。

从图3可以看出，(1)Cyg X-1存在420 d的光变周期，但是误差范围较大(HWHM≈120 d);(2)功率谱分析法容易带来不真实的信息。利用Jurkevich法分析1997年12月～2001年7月间的ASM资料及图3［1］中采用的数据，MJD=50786－52121)的结果表明(图4)，当满足Kidger最小时间跨度时，得到了与图2(b)近似一致的结果，不满足时，最小值明显发散。另外，从图4还可以看出，p≈363和p≈420时出现了最小值。由于363 d和420 d不能满足Kidger最小时间跨度要求，二者都有可能是真实光变周期处最小值的发散导致的。从图2可以看出，Cyg X-1的光变曲线存在363±11.5 d的光变周期及其倍数周期，但420 d的光变周期并没有发现。鉴于以上原因认为420 d的光变周期可能是观测数据分布带来的，而不能准确反映Cyg X-1的光变特性，363±11.5 d才是Cyg X-1的光变周期。

图3 Cyg X-11997年12月至2001年7月间的功率密度谱［1］Fig.3 The Power Spectrum Density for Cyg X-1 during December 1997 to July 2001

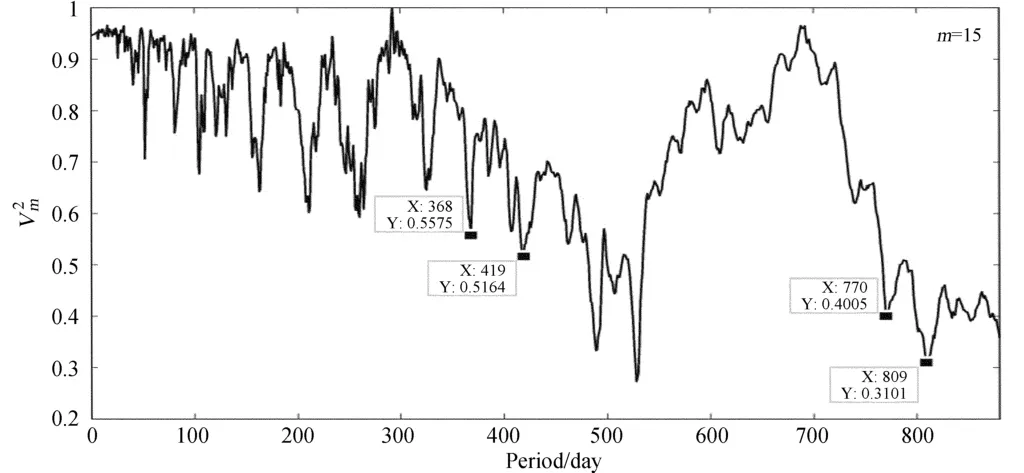
图4 m=15时，试验周期步长为1 d的p－曲线Fig.4 The p－curve for m=15 and step of tiral period=1 day

图5给出了试验周期从1 d到1200 d，步长为10 d的p－曲线。从图中可以看出Cyg X-1存在51±1.4 d的光变周期，但是150 d的光变周期并不存在。因此认为图2出现的51±1.4 d的光变周期才是Cyg X-1真实的光变周期，而102±0.9 d、153±0.9 d和314±5 d的光变周期只是其观测表象而已。

图5 m=15时，试验周期步长为10 d的p－曲线Fig.5 The p－curve for m=15 and step of tiral period=10 day

4 结论

Jurkevich法是一种处理非等时间间隔观测数据十分有效的频谱分析法。本文利用该方法发现黑洞候选体X射线双星存在363±11.5 d的光变周期。同时认为，利用功率谱得到的150 d的光变周期，只不过是51±1.4 d光变周期的观测表象。

［1］Benlloch S，Pottschmidt K，Wilms J，et al.Different kinds of long-term variability from cygnus X-1 ［J］.AIP Conference Proceedings，2004，714:61－64.

［2］Jurkevich I.A method of computing periods of cyclic phenomena ［J］.Astrophysics and Space Science，1971，13(1):154－167.

［3］Babadzhanyants M K，Belokon E T.In variability blazars［M］.Cambridge:cambridge university press，1991:384.

［4］Fan J H，Xie G Z，Pecontal E，et al.Historic light curve and long-term optical variation of BL lacertae 2200+420 ［J］.The Astrophysical Journal，1998，507(1):173－178.

［5］Jurkevich I，Usher P D，Shen B S P.On the light variations of seyfert galaxy 3C120 ［J］.Astrophysics and Space Science，1971，10(3):402－410.

［6］樊军辉，苏成悦.NGC 4151的长期光变行为 ［J］.天文学报，1998，39(3):251－255.Fan Junhui，Su Chengyue.The long-term behavior of optical variability of NGC 4151 ［J］.Acta Astronomica Sinica，1998，39(3):251－255.

［7］张雄，谢光中，白金明.类星体3C345的光变周期特性研究 ［J］.天文学报，1998，39(3):256－264.Zhang Xiong，Xie Guangzhong，Bai Jinming.A study of the light curve periodic behavior of quasar 3C345 ［J］.Acta Astronomica Sinica，1998，39(3):256－264.

［8］樊军辉，Romero G E，林瑞光.3C273的光学光变周期 ［J］.天文学报，2001，42(1):9－15.Fan Junhui，Romero G E，Lin Ruiguang.The optical variability periodicity analysis of 3C273［J］.Acta Astronomica Sinica，2001，42(1):9－15.

［9］陶隽，钱伯辰，梁兆刚，等.判定光变周期的一种方法 ［J］.中国科学院上海天文台年刊，2004，25:97－103.Tao Jun，Qian Bochen，Liang Zhaogang，et al.A method used for finding the period of the light curve ［J］.Annals of Shanghai Observatory Academia Sinica，2004，25:97－103.

［10］毛李胜.3C120射电光变曲线中的一个可能周期 ［J］.天文研究与技术——国家天文台台刊，2007，4(4):307－312.Mao Lisheng.A possible periodicity in the radio light curves of 3C120 ［J］.Astronomical Research ＆ Technology——Publications of National Astronomical Observatories of China，2007，4(4):307－312.

［11］刘凯博，杨东末，侯德东，等.Jurkevic方法在3C120天体光变周期分析中的应用 ［J］.云南师范大学学报，2009，29(5):1－16.Liu Kaibo，Yang Dongmo，Hou Dedong，et al.Computing the period of light variability in seyfert galaxy 3C120 using the jurkevich method ［J］.Journal of Yunnan Normal University，2009，29(5):1－16.

［12］徐云冰，张雄，李孝攀，等.BL Lac天体ON 231的光变周期研究 ［J］.天文研究与技术——国家天文台台刊，2010，7(4):283－289.Xu Yunbing，Zhang Xiong，Li Xiaopan，et al.A study of the periodicity of the light curve of the BL lac object ON 231 ［J］.Astronomical Research ＆ Technology——Publications of National Astronomical Observatories of China，2010，7(4):283－289.

［13］Kidger M，Takalo L，Sillanpaa A.A new analysis of the 11-year period in OJ287-confirmation of its existence ［J］.Astronomy and Astrophysics，1992，264(1):32－36.

［14］Fan J H，Xie G Z，Wen S L.The relativistic beaming model for active galactic nuclei［J］.Astronomy and Astrophysics Supplement Series，1996，116(3):409－415.