大射电望远镜FAST风环境数值模拟研究*

吴明长，王启明，郭永卫，赵保庆

(中国科学院国家天文台，北京 100012)

计划在中国贵州某喀斯特洼地内建设的500 m口径球面射电望远镜FAST，通过主动控制在观测方向形成300 m口径瞬时抛物面。采用光机电一体化的索支撑轻型馈源平台及平台内二次调整装置，在馈源与反射面之间无刚性连接的情况下，实现高精度的指向跟踪［1－3］。其主动反射基准面为半径300 m、口径500 m的球冠。在主动反射面初步设计过程中，风荷载是FAST反射面主要外部载荷［4］，需要进行抗风设计，而现行建筑设计规范GB 50009-2001［5］中并无合适的抗风设计体型系数，因此需要通过数值模拟获得抗风设计的依据。针对FAST进行的风环境模拟前期研究［6］，给出了FAST反射面风压系数随风向的变化，同时给出了FAST索网结构的风振响应初步分析。但随着项目的进展，该研究结果已不能满足工程需要，需要进行更深入的研究。

目前，现场测试、风洞试验、数值模拟是获得建筑物风压系数的3种途径。现场测试最为直观和真实，但耗费人力物力时间较多。存在如何布置测点，某些关键位置难以布置测点及获得结果种类有限的问题。风洞试验成本高，而且由于边界层风洞模拟的局限，结果是否可靠还存在争议［7］。基于计算流体动力学(Computational Fluid Dynamics，CFD)的数值模拟存在边界条件难以符合实际情况，理论模型欠完备等缺点。尽管如此，CFD数值模拟成本相对较低，可以给出很多无法测量的结果，对分析流场规律和特点有着难以替代的作用。本文给出了射电望远镜FAST风环境数值模拟的主要结果，探讨了有关FAST风环境的影响因素和规律。

1 数值模拟方法与模型

1.1 理论模型

大气边界层内绕建筑物流动的空气可以假设为低速、不可压的粘性牛顿流体，基本控制方程是质量守恒方程和动量守恒方程［8］:式中，Sm是质量源项;ρ是静压;τij为应力张量，可以用速度和坐标分量表达;ρgi是重力;Fi是其它体积力或用户自定义源项。

计算流体动力学软件FLUENT［9］基于有限体积法，将计算域离散化为一系列控制体积，在控制体上求解质量、动量、能量、组分等通用守恒方程，将偏微分方程组离散化为代数方程组，用数值方法求解偏微分方程组以获取流场参数的离散数值解。然而，由于实际湍流流场的复杂性，在求解过程中，直接求解这些方程组，尤其是动量方程组，对计算机计算能力要求很高，因此在工程应用中，一般将湍流各变量在时域看作平均和脉动两部分，将动量方程逐项平均得到不封闭的雷诺方程，并且提出多种湍流封闭模式求解这些雷诺方程［9］。不同的湍流封闭模式有着不同的特点，常用的几种模型在预测钝体表面风压分布时结果差别不大。因此，尽管标准k-ε模型对于分离的预测不够准确，但由于工程应用精度要求不高，并且由于标准k-ε模型工程上应用广泛，所以本文有关计算中一般采用标准k-ε模型。

1.2 几何模型

经过分析试算，确定了将口径500 m的FAST反射面和水平尺度约3 km×3 km的山体模型放置于XYZ方向尺度分别为40 km×10 km×5.5 km的计算域中。其中，来流方向的计算域尺度为40 km，反射面中心位置距离来流入口20 km，垂直于来流方向的计算域尺度为10 km，计算域底部海拔为500 m，顶部海拔为6000 m。为减小网格划分的难度并减小计算量，将计算域分为外部和内部两个。

保持坐标系及内部计算域和计算对象不变，旋转外部计算域至不同角度，可方便地获得用于不同风向工况计算的几何模型，在此基础上形成网格模型和CFD计算模型。风向约定沿用地学中常用的表达习惯，以正北为0点钟或12点钟方向，正东为3点钟方向。X轴正向指向3点钟方向，Y轴正向指向12点钟方向，Z轴正向竖直向上。以3点钟方向为例，外部计算域和内部计算域的相对位置关系如图1。其中，中心区域包含了FAST反射面结构、山体表面及可能的挡风墙结构，如图2。

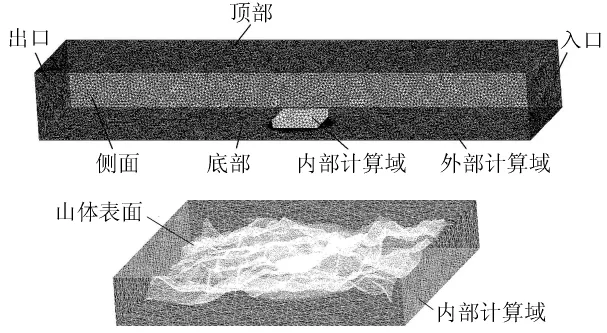
图1 3点钟风向下外部计算域和内部计算域Fig.1 External and internal calculation domains with the wind direction of 3 o’clock

图2 山体表面、FAST反射面及挡风墙结构的几何模型(a)3 km×3 km山体表面;(b)中心350 m范围开挖后地形;(c)FAST反射面在洼地内的相对位置;(d)不同高度、不同径向位置的挡风墙Fig.2 Geometric model of the hill surface，the reflector of FAST，and the windbreaks(a)Hill surface of 3km×3km;(b)The excavated terrain within 350m from the center;(c)The relative position of the reflector in the depression;(d)Windbreaks of different heights and radial positons

1.3 网格模型

山体表面形状本身是不规则的，反射面临近地域在开挖后带来更多片状不规则区域，这种不规则性，给几何建模、网格划分及生成有效的CFD计算模型带来困难。采用分区划分及非结构化网格划分的方法，获得了多种计算工况下的网格模型，典型网格划分结果的部分表面网格见图3。相应的网格设置如表1，不同范围的边界之间，通过网格划分软件的边界网格一致功能实现。

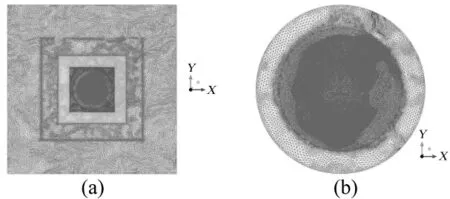
图3 地形表面的网格(a)山体表面网格，由外到内逐渐加密;(b)距离反射面中心350 m范围内的地表网格Fig.3 The CFD mesh grid at the surface of the terrain(a)Mesh grid at the hill surface(appearing denser in the inner area);(b)The mesh grid at the terrain surface within the radial distance of 350m from the center

表1 不同地形范围内的网格大小设置Table 1 The mesh sizes for the different regions of the terrain surface

1.4 边界条件

计算域入口边界条件采用剪切流风剖面，根据建筑物结构荷载规范GB 50009-2001，近地面风速沿高度方向近似按指数分布，如下式:

对于山地和丛林，指数α取0.16，速度基准高度Vb一般以地面以上Zb=10 m计，Vb取规范中要求的极限风速14 m/s。

来流湍流强度采用澳大利亚规范中第2类地貌的取值，

显然，来流速度和湍流特性与坐标相关，这种变化的边界条件在FLUENT软件中可以通过用户自定义函数(User Defined Function，UDF)实现。

为保证植被光照需求，所设计的FAST反射面其透孔率约为35.4%。反射面各单元是多孔薄面板形式，相对于总体尺度，1.2 mm板厚和5 mm孔直径非常小，而且孔的数量又很多，试图直接将孔的模型反映在计算模型中是不现实的，直接忽略也缺乏依据。为了考察反射面板透孔率对流场的影响，在后文中尝试使用FLUENT软件中多孔介质跳跃的边界条件模拟透孔反射面的空气动力学特性。具体做法是首先通过数值模拟计算空气流过透孔面板后压降随速度的变化关系，然后根据这种速度压降关系，计算得到多孔介质跳跃的边界条件所要求的面渗透性α和惯性阻力因子C2。出口采用完全发展边界条件，即流场任意物理量沿出口法向梯度为0。计算域顶部和底部取自由滑移的运动壁面条件，地面和物体表面取静止壁面条件。

考虑到山体表面岩石、树木等不平整因素的影响，将山地表面分为两个区域，距离反射面中心350 m之外和之内两部分。因为350 m之内大部分需要开挖和施工，基本没有高大树木等，取较小的粗糙高度，而对350 m之外的部分，则取较大的粗糙高度。

2 计算方法和结果

计算中采用基于压力的求解器，稳态计算，湍流模型采用标准k-ε模型，采用标准壁面函数近似处理近壁网格划分不够细致的问题。计算过程中根据实际迭代情况，调整松弛因子，一般收敛准则为残差小于1×10－3，同时以关键物理量是否稳定作为收敛与否的判据。

首先通过分析和试算确定了入口速度计算的基准高度，然后利用数值模拟获得了FAST反射面透孔面板的速度压降特性，并以此为基础计算了是否考虑面板透孔率两种情形的反射面风压系数分布特点及其与风向的关系，最后给出了挡风墙效果数值模拟研究的部分结果。

2.1 基准高度对计算结果的影响

确定计算域入口速度剖面时，由于FAST台址洼地地表起伏很大，不能作为CFD分析模型中Z向坐标的起点。需要引入基准高度Hb，才能恰当描述计算域入口速度剖面，如下式:

结合山地表面海拔高度，以及计算域顶部和底部的海拔高度，对若干不同Hb值进行了试算，得到反射面下表面和上表面风压系数之差与Hb的关系，如图4。

首先，基准高度应小于所涉及的地形边界的最低海拔高度，对本文所涉及的地形，这个高度约为810 m。另外，由图4可以看出，在810 m上下40 m的变化范围内，反射面风压系数的极值和均值对参考高度是不敏感的，因此后续计算中，一系列分析计算中基准高度Hb的取值均为810 m。

2.2 透孔面板的速度压降特性

图4 反射面下表面、上表面风压系数差值与基准高度的关系(其中，Diff表示下表面减去上表面的差值，Diff Min表示在整个反射面范围内各计算节点上这个差值的最小值，Diff Max表示相应的最大值，Diff Aver表示这个差值的平均值，Diff RMS表示这个差值的均方根值，下同)Fig.4 The relation between the wind pressure coefficient difference from the upper to lower surfaces of the reflector and the reference altitude(The“Diff”denotes the wind pressure coefficient of the lower surface subtracted by the one of the upper surface.The“Diff Min”，“Diff Aver”，and “Diff RMS”denote the minimum，the average，and the rms values of the coefficient differences between the reflector surfaces)

FLUENT软件提供了多孔介质跳跃边界条件，用于模拟速度或压降特性均为已知的薄膜，是多孔介质模型的一维简化，可用于流体通过筛子、过滤器、过滤纸和多孔板的压降模拟。这种边界类型需要设置面渗透性数值α、介质厚度t、压力变化系数C23个参数。

对于简单各项同性多孔介质，流体流过多孔介质的压降Si由粘性损失和惯性损失两部分组成［9］(实际应用中应考虑介质厚度t)，除物性参数μ和ρ外，面渗透性α和惯性阻力因子C2是需要求解的。

另外，物理实验表明，流体穿过多孔板或丝网的压降与速度成二次函数关系:

通过物理实验获得惯性阻力项系数a1和粘性阻力项系数a2后，就可以通过对比获得面渗透性α和惯性阻力因子C2。

因此，为了以多孔介质跳跃边界条件表示FAST反射面，首先需要获取描述速度和压降特性的系数a1和a2。另外，既然物理实验可以获得这样的压降关系，在条件有限的情况下，也可以通过数值模拟近似获得a1和a2的值。对于FAST反射面板的某局部孔来说，周围的孔允许空气的流出，所以在建立空气流过孔板的CFD模型时，应允许空气自由地从孔板周边流过。图5给出了若干不同流速下，空气流过FAST孔板(透孔率35.4%)的压降。

根据速度压降特性，就可以通过二次曲线拟合得到惯性阻力项系数a1和粘性阻力项系数a2，并通过对比获得面渗透性α和惯性阻力因子C2。

气动系数K值可以通过速度压降特性拟合得出，所得K值可以与Dryden H L和Schubauen G B于1947年的实验结果作对比［10］(图6)。由图6可以看出，35.4%透孔率的FAST反射面面板的数值模拟结果与实验结果误差小于3%。

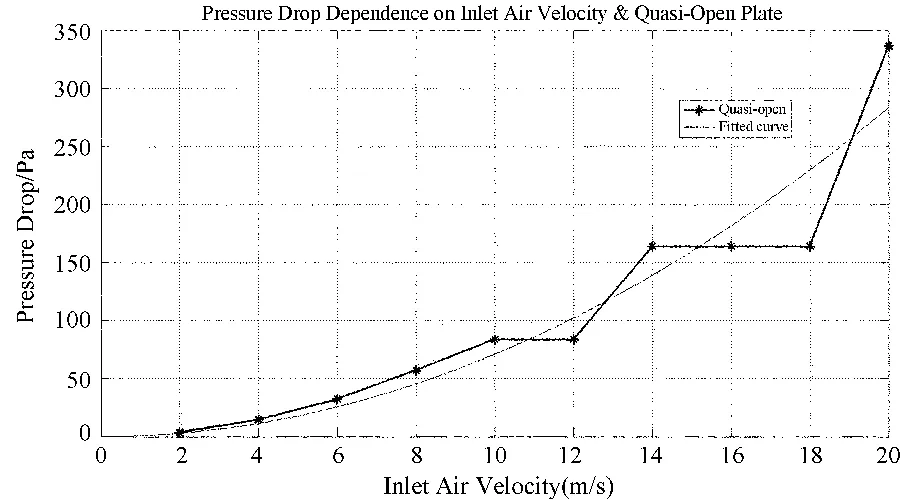
图5 FAST反射面板的速度压降特性曲线Fig.5 The simulated relation between the wind-pressure drop and the wind speed for the FAST reflector panel under consideration

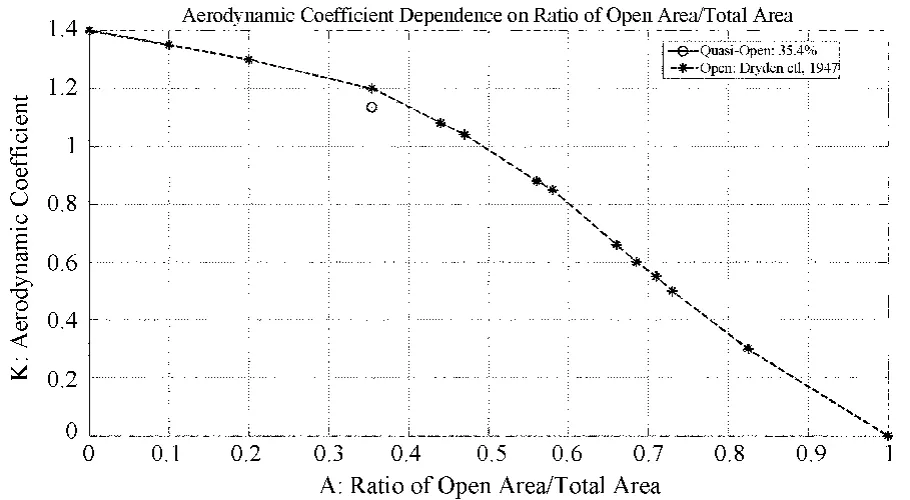
图6 FAST反射面板气动系数值与实验结果对比Fig.6 The comparison of the simulated aerodynamic coefficients of the FAST reflector panel to experimental results from references

由于FAST反射面板的厚度和孔径相比较小，并且不同来流方向等效透孔率近似相等，所以平面孔板的数值模拟和实验结果用于模拟空气流过FAST球冠形透孔反射面的流动特性时具有一定的合理性，空气是否垂直流向面板可以作为次要因素忽略。

2.3 面板透孔率对反射面风压分布的影响

进行FAST反射面附近空气流场特性数值模拟时，究竟是否需要考虑反射面面板的透孔率，需要通过比较才能给出结论。图7给出了5点半风向下(该风向为通过不同风向比较计算确定的不利风向)，不考虑反射面透孔率和35.4%透孔率两种情形的反射面风压系数的分布特点，可以看出孔的存在总体效果是均化了反射面风压系数分布。

FAST所处地域山地地表海拔高度差异很大，不同风向下反射面的风压系数分布应当有所差异，图8给出了是否考虑反射面透孔率两种情形下，反射面风压系数随风向的变化。

从图8可以看出，其一，考虑反射面透孔率时，反射面风压系数的极值明显减小;其二，不考虑反射面透孔率时，不利风向约为5点半方向，考虑反射面透孔率时，不利风向约为5点半方向和9点半方向。

图9给出了是否考虑反射面透孔率两种情况下，各风向下反射面风压系数沿半径方向的统计。

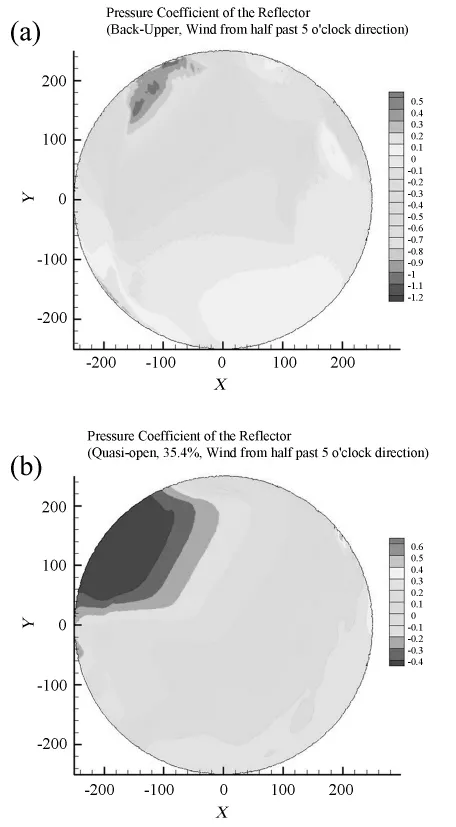
图7 是否考虑面板透孔率两种情形下反射面风压系数分布(a)不考虑反射面透孔率;(b)反射面透孔率35.4%Fig.7 The wind pressure coefficients of the reflector panel for the two cases of perforation rate.(a)null perforation，and(b)35.4%perforation rate

图8 是否考虑面板透孔率两种情形下反射面风压系数随风向的变化(a)不考虑反射面透孔率;(b)反射面透孔率35.4%Fig.8 The wind pressure coefficients of the reflector panel for different cases of perforation rate and different wind directions.(a)null perforation，and(b)35.4%perforation rate

图9 是否考虑面板透孔率两种情形下各风向反射面压力系数沿半径方向的统计(a)不考虑反射面透孔率;(b)考虑反射面透孔率35.4%Fig.9 Statistics of the wind pressure coefficients at various radii of the reflector panel for different cases of perforation rate under and different wind directions.(a)null perforation，and(b)35.4%perforation rate

可以看出，与不考虑面板透孔率的情况相比，35.4%透孔率的反射面面板的风压系数从远离球心的压力为主(负值)转为指向球心的压力(正值)为主。

2.4 挡风墙问题

一般认为在反射面周边适当位置设置挡风墙能对某些山口的风速起到阻挡作用，从而改善反射面风压环境。实际挡风墙效果如何，需要通过计算或试验才能确定。

以距离中心275 m位置为例，在高度方向，根据挡风墙上沿与反射面边沿的相对位置分为:高出边沿10 m和5 m，与边沿平齐(0 m)，低于反射面边沿5 m、10 m、15 m、20 m，以及低于反射面边沿40 m(无挡风墙)共8种情形，如图10。另外，还可以考察同样的挡风墙高度，挡风墙距反射面中心不同位置处的效果，如图11。

图10 不同高度挡风墙对反射面下表面、上表面风压系数差值的影响(距离中心275 m)Fig.10 Results of the wind pressure coefficients for different heights of the windbreaks.(All for the position of275m from the center of the reflector)

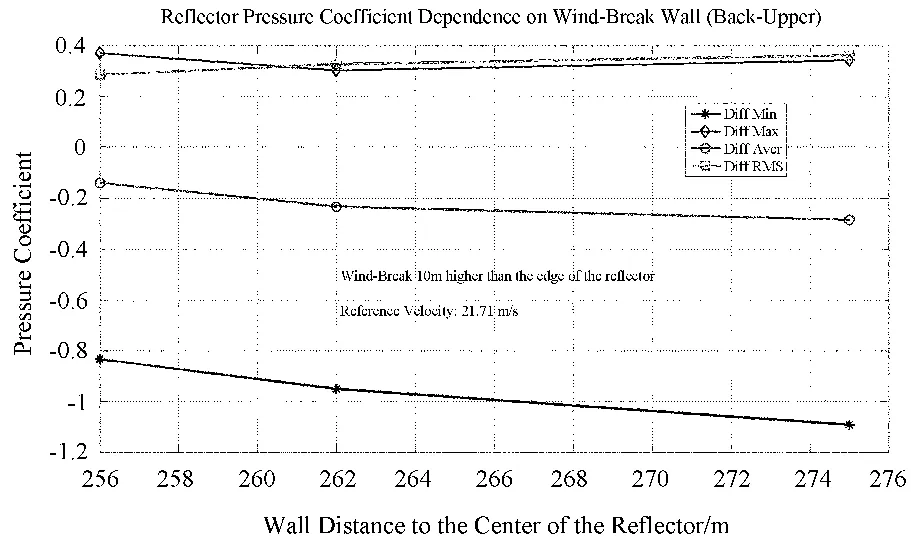
图11 不同位置挡风墙对反射面下表面、上表面风压系数差值的影响(挡风墙高出反射面边沿10 m)Fig.11 Results of the wind pressure coefficients for different positions of the windbreaks.(All for a height of windbreak of 10m above the edge of the reflector)

从图10和图11可以看出，挡风墙高度变化对反射面风压系数极值改变的效果大于挡风墙径向位置改变的影响。这说明建设挡风墙时，挡风墙距中心位置的距离选择要求稍低。

此外，挡风墙效果如何，还要看其对反射面风压系数分布的影响。图12给出了反射面透孔率为35.4%时无挡风墙和有挡风墙的反射面风压系数分布特点对比。除了少数局部位置有所变化外，总体范围差异并不明显。

图12 考虑反射面透孔率35.4%时，无挡风墙和有挡风墙的效果(a)无挡风墙;(b)距离275 m处高出边沿10 m的挡风墙Fig.12 Contours of wind pressure coefficients for the panel of 35.4%perforation rate with and without windbreaks(a)without windbreaks，and(b)with a windbreak at a distance of275m from the center and with a height of 10m above the edge of the reflector

3 结果分析和讨论

对于考虑反射面透孔率的情况，采用多孔介质跳跃边界条件模拟反射面，FLUENT计算结果给出的是上下表面之差，风压系数规定指向上部(球心)为正值。而当不考虑反射面透孔率时，就需要计算反射面两个侧面风压系数差值，同样以指向上部(球心)为风压系数正值。这样，反射面某部分承受正风压时，说明该部分承受的是指向球心的风压，反之，反射面某部分承受负风压时，说明该部分承受的是远离球心的风压。

对于CFD计算模型，边界条件和物理属性是建立在简化和假设之上的，这决定了它获得的总是依赖于模型的离散近似解。首先，计算依据的地形数据经过空间域采样和插值等必要处理后存在误差，计算中采用的几何模型和实际对象的差异会带来几何模型的误差。其次，对几何模型进行网格划分，有限的网格是对连续的几何模型的一种近似，这是离散误差。再次，计算中涉及的边界条件，如来流特性和壁面属性等，均与实际情形有差异。最后，数值计算过程中，数据截断和舍入误差，控制终止条件而导致的迭代误差等均是CFD数值模拟中的误差来源。

如果CFD数值模拟对象较为简单，则有可能结合试验或理论结果进行一定的误差估计，但是对于本报告涉及的FAST风环境模拟，这两种方法均不可行，试验也仅仅能给出一部分的规律性结果，难以给出精确的结果。

因此，本文给出的模拟计算的结果其意义在于分析FAST临近地域风环境的规律和特点，为后续抗风设计做准备，体现在以下几个方面:

(1)通过分析和计算确定了810 m为计算基准高度。

(2)35.4%透孔率反射面板的速度压降特性数值模拟结果与前人实验结果一致性很好。是否考虑反射面透孔率，结果有较大差异。

(3)不同风向下反射面风压系数差异较大，将不利风向5点半方向作为各种分析的基本风向。

(4)建设挡风墙时，距中心位置距离的选择要求较低。

这些分析和计算结果为后续反射面受风荷载的变形计算以及反射面高精度测控打下了基础。

4 结论

本文针对FAST反射面及其周边山地地形，建立了几何模型、网格模型和CFD分析计算模型。通过分析和试算确定了入口风速剖面的基准高度为810 m。并通过数值模拟获得了35.4%透孔率的FAST反射面板的速度压降关系，气动系数结果与前人实验结果误差小于3%。模拟计算了不同风向下反射面风压系数分布特征，得出的不利风向为5点半方向。研究还表明，挡风墙高度选择的效果优于位置选择的效果。

致谢:感谢Richard David先生提供文献数据来源。感谢计算机网络信息中心超级计算中心提供软硬件计算资源。

［1］南仁东.500 m球反射面射电望远镜FAST［J］.中国科学G辑，2005，35(5):449－466.

［2］FAST项目组.FAST初设总册 ［R］.北京:中国科学院国家天文台，2008.

［3］Nan Rendong，Li Di，Jin Chengjin，et al.The Five-Hundred-Meter Aperture Spherical Radio Telescope(FAST)Project［J］.International Journal of Modern Physics D，2011，20(6):989.

［4］FAST项目组.500 m口径球面射电望远镜(FAST)项目初步设计(主动反射面分册)［R］.北京:中国科学院国家天文台，2008.

［5］中国建筑科学研究院.建筑结构荷载规范(GB50009-2001)［S］.北京:中国建筑工业出版社，2006.

［6］林斌，范峰，钱宏亮.大射电望远镜FAST主动反射面在喀斯特地貌下的绕流数值模拟及其风振响应分析［C］//第四届全国现代结构工程学术研讨会论文集.宁波，2004.

［7］魏庆鼎，陈凯，卢占斌，等.风洞模拟大气边界层的若干问题 ［C］//第11届全国结构风工程学术会议论文集.三亚，2004.

［8］贺德馨.风工程与工业空气动力学 ［M］.北京:国防工业出版社，2006.

［9］Fluent6.3 User's Guide ［EB/OL］.http://www.ansys.com/products/fluid%2Ddynamics/fluent/.

［10］Dryden H L，Schubauen G B.The Use of Damping Screens for the Reduction of Wind Tunnel Turbulence ［J］.Journal of the Aeronautical Sciences，1947，14(2):221－226.