控制动作下带缆遥控水下机器人的水动力特性*

吴家鸣 崔寅，3 邓威 伍力 马志权

(1.华南理工大学土木与交通学院，广东广州510640;2.广州市番禺灵山造船厂有限公司，广东广州511473;3.秦皇岛出入境检验检疫局，河北秦皇岛066004)

带缆遥控水下机器人是一种日益广泛应用于浅海海洋环境动态监测的水下探测装置，它在水下观测、海洋研究与海洋环境调查中有着特殊的用途.带缆遥控水下机器人通常由脐带缆、水下机器人和机器人轨迹与姿态控制机构组成.水下机器人所配置的监测传感器的工作性质要求机器人工作时姿态稳定，并具有快速灵活的轨迹和姿态调节与控制能力.研究者为开发符合这种要求的带缆遥控水下机器人做了大量的工作;建立准确的带缆遥控水下机器人控制模型，以此预报机器人在一定控制动作下的水动力特性是开发性能良好的带缆遥控水下机器人的必要前提.

近年来，国内外的研究人员进行了不少关于带缆遥控水下机器人水动力特性方面的探讨.但是，对带缆遥控水下机器人水动力数值模型方面的研究主要集中在对机器人的单一部分，例如脐带缆、水下机器人主体或轨迹与姿态控制机构的研究等［1-3］，而对于如何从整体的角度对带缆遥控水下机器人进行系统的分析和研究，目前还缺乏深入的探讨.在水下机器人的控制方面，目前的研究也仅局限在简单的水动力数学模型的基础上，以施加于水下机器人上的总力为控制目标，对于多自由度轨迹和姿态同步控制的相关研究也较少.

基于这一背景，文中在笔者课题组所建立的完整带缆遥控水下机器人水动力数学模型的基础上［4-5］，引入由模糊神经算法构建的控制器，组成带缆遥控水下机器人的控制系统，以神经网络相关理论结合计算流体方法对推进力和转速之间的相互关系进行辨识和换算，对带缆遥控水下机器人多自由度上的轨迹和姿态控制进行数值模拟计算.

1 水动力数学模型及其主要数值方法

1.1 水动力数学模型的整体思路及机器人系统的基本构成

文中的水动力数学模型中，脐带缆的运动控制方程采用 Ablow 等［6］提出的模型，并用 Gertler等［7］提出的水下运载体六自由度运动方程来描述水下机器人的水动力状态.以脐带缆的运动控制方程为核心，通过引入脐带缆和工作母船以及水下机器人连接点的边界条件，将脐带缆模型和水下机器人运动方程联系到一起，从而建立整个系统的水动力数学模型.对模型中作用在机器人主体上的水动力载荷和旋转导管螺旋桨的控制力，在考虑它们之间的相互影响的基础上以计算流体力学方法求出.水动力数学模型建立的整体思路和方法见文献［4-5］.

所研究的带缆遥控水下机器人主体为一椭球体，主体上配置了4个控制导管螺旋桨，其编号见图1.4个螺旋桨分置于与机器人局部坐标xOy平面垂直的主体4个面的中心处，它们的序号分别为1－4号螺旋桨，脐带缆连接于椭球型机器人主体的上端，机器人系统中所使用的导管螺旋桨为Ka 4-70/19A.脐带缆、水下机器人主体和螺旋桨的计算参数如表1所示.

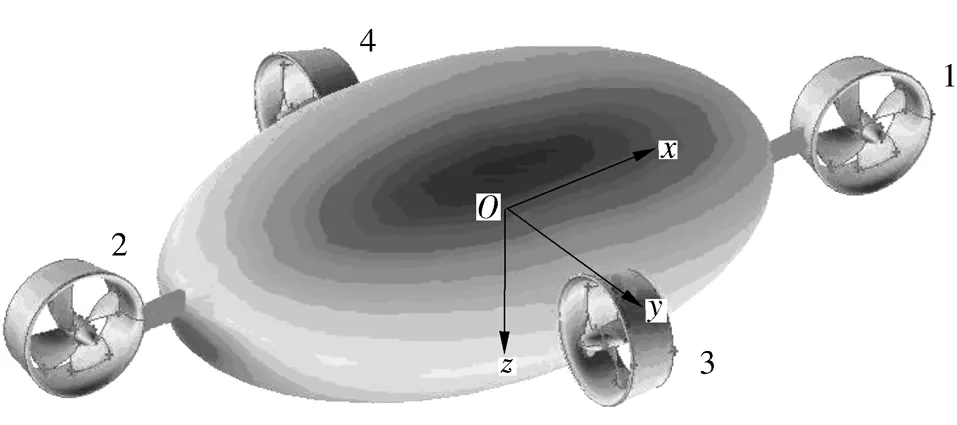
图1 水下机器人的布置结构Fig.1 Structural layout of underwater robot

表1 带缆遥控水下机器人的计算参数1)Table 1 Computational parameters of tethered underwater robot

1.2 作用在机器人主体上的水动力载荷和导管螺旋桨的推进力

通过计算流体力学方法得到作用在水下机器人上的水动力载荷和导管螺旋桨的控制力的数值解.首先根据所要计算的水下机器人及其相连的导管螺旋桨的几何要素，构造机器人和导管螺旋桨的三维几何模型［8-9］，在此基础上借助计算流体力学软件Fluent在机器人、导管和螺旋桨所在的流域内求解其流体力学控制方程，以此计算作用在水下机器人主体上的水动力载荷以及水下机器人主体流场作用下导管螺旋桨在一定转速和一定来流方向下所产生的推力与转矩.

1.3 计算域的确定

数值计算作用在水下机器人上的水动力载荷和导管螺旋桨的控制力时，将机器人主体置于计算域的中心，控制导管螺旋桨附连于机器人主体上，计算域尺度的选择应以足够避免水下机器人系统周围与边界流场之间的干扰为准则.计算所用计算域的网格如图2所示，计算域的具体构造方法见文献［10］，每一时间步作用在水下机器人上的水动力载荷和导管螺旋桨的控制力的具体计算方法与计算技术可参见文献［4］.

图2 整个计算域的网格划分Fig.2 Mesh division of the whole computational domain

2 控制系统的设计

文中所研究的带缆遥控水下机器人的控制系统是针对带缆遥控水下机器人在水平面三自由度(即绝对坐标系下水平面轨迹和首摇角)上的运动控制而设计的，包括一个控制器和一个逆系统模型网络，其特点是建模、学习和工作的过程分两步进行:第一步，构建一个模糊神经网络，并用先验知识训练使它能达到模拟被控对象(即带缆遥控水下机器人)运动的逆动态特性，这一步是离线训练过程，通过给模糊神经网络输入带缆遥控水下机器人的输出信息和控制信息组成的样本集来实现;第二步，在构建完这样一个水下机器人的逆系统后，使用其来训练控制器以完成控制系统的建模.

2.1 模糊神经网络控制器

模糊神经网络控制器的设计中需要确定控制器的输入输出参数和控制算法.因为文中设计的控制器是模拟水下机器人的逆系统，所以其输入和输出参数对应于水下机器人的输出和输入参数，即控制器以水下机器人输出的运动参数(速度和加速度)为输入，以达到期望轨迹所应施加于水下机器人上的力及力矩为输出.又由于该控制系统是针对水下机器人三自由度运动的控制，故相应输入为三自由度的速度和加速度.文中采用标准模型的模糊神经网络，其基本结构及原理可参考文献［11］.

2.2 期望轨迹姿态的规划

设水下机器人的位置状态变量为X，V为水下机器人的运动速度，

其中，X0、Y0、ψ0分别为绝对坐标下水下机器人的水平面位置坐标和首摇角，VX、VY、Vψ为机器人运动速度在相应自由度的分量.

设水下机器人的期望变量为Y，

其中，Xd、Yd、ψd为机器人水平位置坐标和首摇角的期望值.则水下机器人的位置偏量S可定义为

因此可以将预先规划的输出表示为ad=f(S，V).文中采用的ad的具体形式为［12］

其中:amax为限制水下机器人的最大加速度，其取值主要取决于水下机器人的推进系统即螺旋桨的布置和性能;P为三阶对角矩阵，

其中

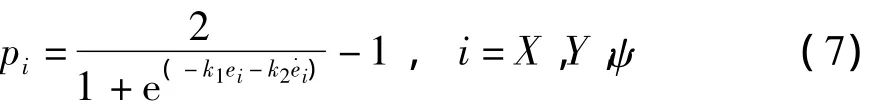
k1和k2是需要人工调节的待定常数，而ei和定义为

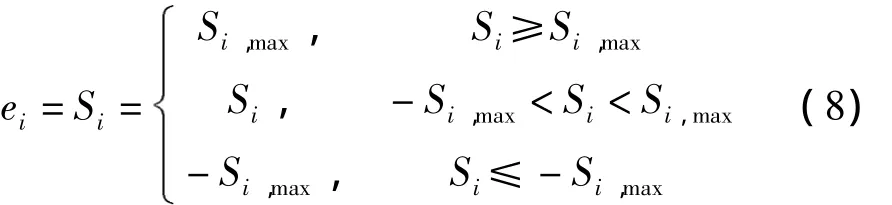
其中:Si，max为一待定常数，其值为根据设计而限制水下机器人运动的最大值;Si为式(4)定义的机器人的位置偏量.

2.3 螺旋桨推力分配和转速换算

由于所需要实现的控制目标为水下机器人三自由度上的运动，故布置了两对螺旋桨位于水下机器人局部坐标系下的xOy平面内，两对螺旋桨的轴线方向分别对应于x轴和y轴方向.设1－4号螺旋桨对应的推进力分别为 T1、T2、T3和 T4，T1和 T2位于xOy平面内，实现的是沿y轴的平动和绕z轴的转动，T3和T4也位于xOy平面内，用于实现沿x轴的平动和绕z轴的转动，如图3所示.

图3 三自由度运动的螺旋桨的推进力布置Fig.3 Sketch of propeller propulsion in three degrees of freedom

则其合力Tx、Ty和合力矩NT可表示为

其中，R1、R2、R3和R4为对应螺旋桨与平行的坐标轴之间的垂直距离，由于每对螺旋桨都是对称布置结构，所以 R1=R2=R12，R3=R4=R34.方程(10)中等号左端即为控制器对规划后的期望轨迹姿态的控制输出，由于螺旋桨1和2的力臂R12要大于螺旋桨3和4的力臂R34，即螺旋桨1和2相对于3和4只需要较小的力便可满足对ψ方向上的转动要求，所以绕z轴的转动只依靠螺旋桨1和2产生的力矩控制，则设计

对于螺旋桨1和2，则有

在带缆遥控水下机器人运动的某一特定时刻，螺旋桨产生的推进力与螺旋桨的转速成正比，即转速越大推进力越大，反之亦然.文中，螺旋桨产生的推进力与螺旋桨转速之间的关系采用一单输入单输出的三层BP神经网络来实现，即以所需推进力为输入、所需对应的转速为输出，隐层节点取为3，网络的输出误差函数采用

其中:Fthd为所需的推进力;Fth为某一转速对应的推进力;k为待定的正常数，其取值应保证网络的可收敛性.此神经网络与Fluent水动力计算模块串联起来即可进行无导师学习.实际数值计算证明，只要k取到合适的值，利用梯度下降算法，可以很快使神经网络输出的转速逼近所需施加推进力对应的真实转速.

3 水下机器人控制过程数值模拟的主要步骤

基于文中所采用的水动力数学模型而建立的带缆遥控水下机器人的水动力与控制模型及其相应的计算程序主要包括三大模块:系统水动力数学模型主程序模块、计算每一模拟时间步中机器人主体所受的水动力载荷以及控制螺旋桨所发出的控制力的计算流体力学模块、控制螺旋桨转速的控制模块.

3.1 主程序模块

以有限差分法求解带缆遥控水下机器人系统水动力数学模型的主程序.该水动力数学模型的核心是脐带缆的动力方程，通过在脐带缆上下两端引入脐带缆动力方程的边界条件而构造出完整的水动力数学模型.该主程序用Fortran语言编写，数学模型的建立及数值解法的基本思路与文献［4-5］类似，在此不再赘述.

3.2 计算流体力学模块

在数值模拟的每一时间步，利用计算流体力学技术，以一种综合、整体的数值模拟手段确定机器人主体与控制螺旋桨相互影响下作用在水下机器人主体的水动力载荷以及螺旋桨所发出的推进力.该部分计算采用计算流体力学软件Fluent的水动力计算模块进行.

3.3 控制模块

控制模块主要基于模糊神经网络的控制算法.本研究利用该算法来控制机器人主体上螺旋桨的转速，使其发出所要求的推进力来达到操纵水下机器人按照操作者的轨迹与姿态要求运行的目的.控制模块的算法利用Matlab平台编写.

3.4 主要计算步骤

根据所建立的水动力与控制模型以及相应的数值算法，可以对带缆遥控水下机器人在控制螺旋桨所发出的控制力作用下的水动力与特性进行数值模拟.根据所编制的计算程序模拟带缆遥控水下机器人在一定的控制动作下水动力特性的主要算法如下:

(1)在主程序中输入带缆遥控水下机器人系统参数，这些参数包括脐带缆、水下机器人以及控制螺旋桨的几何和物理参数.

(2)计算机器人系统在设定条件下的定常解，通过所计算的定常解得到沿脐带缆各节点以及水下机器人在设定条件下的坐标值及方位角，这些参数作为后续时域解的初始值;令n=1，其中n为时间步数.

(3)引入水下机器人在m点的运动轨迹坐标与姿态的期望值，m=1，2，…，RP，其中 m 为由机器人操作者指定的机器人运动轨迹上分布的指定点的序列号，RP为m的最大值.

(4)从上一时间步计算结果中读入n－1时间步时的水下机器人姿态与运动参数、控制螺旋桨的推进力以及水下机器人所受到的水动力.

(5)由方程(2)和(5)对机器人在m点的运动轨迹坐标与姿态期望值的误差进行预先规划，得到ad和水下机器人的运动速度V，并以ad和V作为控制器的输入参数，通过2.3节所介绍的方法，由所设计的控制器确定为使机器人达到m点的运动轨迹坐标与姿态的期望值而在第n时间步时各控制螺旋桨所需要发出的推进力，进而确定其所需要的转速.

(6)利用Fluent水动力计算模块计算在第(5)步所要求的各控制螺旋桨转速下、考虑螺旋桨与机器人主体的相互作用因素时水下机器人在第n时间步所实际受到的水动力和螺旋桨所实际发出的推进力.

(7)将第(4)步和第(6)步确定的n和n－1时间步时水下机器人实际受到的水动力和控制螺旋桨推进力数据传给Fortran计算主程序.

(8)依据第(7)步传入的数据，求解如3.1节所描述的水下机器人系统水动力数学模型的主程序，通过主程序的运算求出在第n时间步下水下机器人系统的姿态和运动参数.

(9)将第n时间步时刻计算出来的水下机器人的姿态和运动参数与期望值对比，如不满足控制误差要求，则令n=n+1，转向第(4)步;如满足误差要求，则转向第(10)步.

(10)若 m≤RP，则令 m=m+1，转向第(3)步;否则输出数值模拟计算结果，计算结束.

4 控制系统的仿真

采用根据上述算法结构所构建的带缆遥控水下机器人的三自由度轨迹与姿态控制系统，对通过控制螺旋桨的转速、在一定的来流速度情况下带缆遥控水下机器人的回转运动进行了数值模拟，分析机器人在螺旋桨产生的控制力和力矩作用下的流体动力特性.水下机器人工作水域水流的流速为0.1m/s，水流方向沿绝对坐标系X轴正向;控制过程中，脐带缆在水面上的上端点位置维持不变，其位置在绝对坐标系中的坐标为:{X，Y，Z}={0.0 m，0.0 m，0.0m};计算中控制时间步长取为0.1 s;计算中作为后续时域解的初始值的脐带缆下端点与机器人连接处的绝对坐标取为

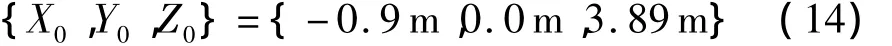
机器人在控制螺旋桨操纵下的水动力特性时域计算由水下机器人处于式(14)所设定的点作为起始点，数值模拟中机器人在控制作业中的轨迹定义为脐带缆与机器人连接点处的绝对坐标.文中对在以下两阶段XOY平面中控制目标下的机器人水动力特性进行了数值模拟:

(1)控制机器人从点{X，Y}={－0.9m，0.0m}到点{X，Y}={－0.75 m，0.0 m}的直线运动，在这一直线运动中机器人的艏向角(机器人局部坐标x轴与绝对坐标X轴之间的夹角)保持为0°.

(2)控制机器人从点{X，Y}={－0.75m，0.0m}出发，沿着以{X，Y}={－0.75m，0.5 m}为圆心、半径为0.5m的轨圆逆时针旋转一周，在这一运动过程中控制机器人的艏向角保持与轨圆相切.

对水下机器人在控制动作下的动力特性进行数值计算.计算分为两个时间段进行:第一时间段持续时间为1～10s，该时间段所进行的是3.4节第(2)步所描述的定常解计算，其目的是为后续控制时域解提供初始值;第二时间段则从10s开始，所进行的计算为满足上述的控制目标而对机器人实施控制所进行的数值模拟计算，图4－13为在该时间段的计算结果.在上述两阶段控制目标下，水下机器人的期望运动轨迹与实际运动轨迹的比较如图4所示，机器人在典型位置上的期望坐标与实际运动轨迹坐标如表2所示，相应的首摇角(ψ)变化的时间历程如图5所示.

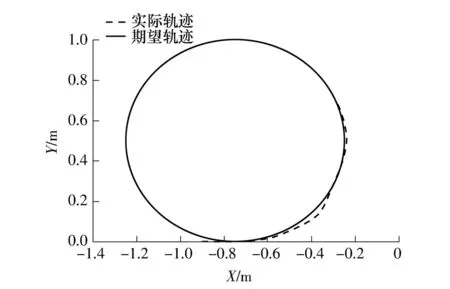
图4 期望轨迹与实际轨迹对比Fig.4 Comparison between expected and real trajectories

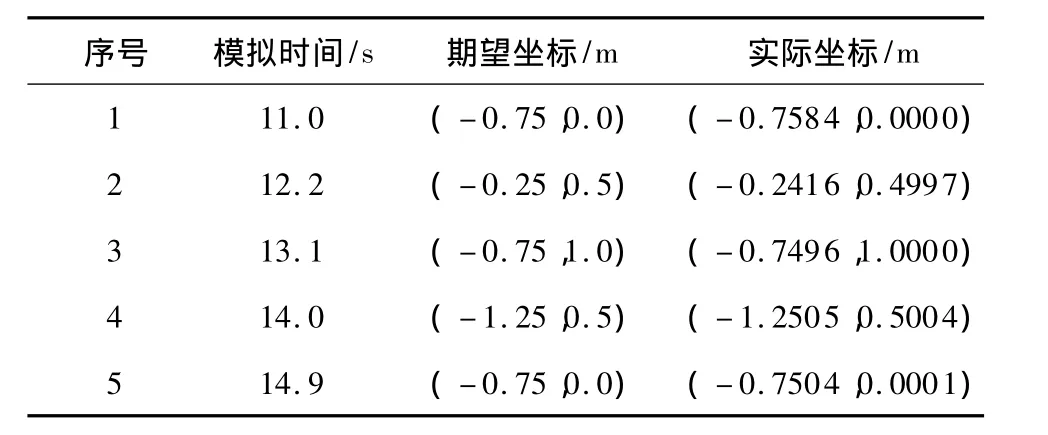
表2 机器人在典型位置上的期望坐标与实际运动轨迹坐标Table 2 Expected and real trajectory coordinates of robot at representative positions

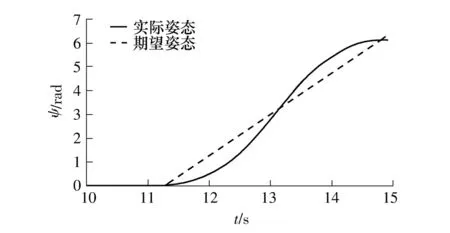
图5 期望姿态与实际姿态对比Fig.5 Comparison of expected and real attitudes

从图4、图5以及表2的模拟结果可以看出，受控机器人运动的轨迹和姿态与期望轨迹和姿态吻合良好，控制结果与期望值的对比表明，采用文中所提出的控制器对带缆遥控水下机器人进行轨迹与姿态控制可以得到理想的控制效果.由于在文中的控制器设计中对机器人艏向角加速度变化的最大值设置了限制，因此对艏向角的控制有一定的滞后，从而导致了期望姿态与实际姿态存在一定的差异，但笔者认为这一误差在可接受的范围内.

机器人在控制过程中绝对坐标中的速度分量以及艏向角速度变化的时间历程如图6和7所示.对比图4、表2和图6的结果可以看出，机器人在绝对坐标中的运动速度与其运动轨迹变化关系一致;图7的模拟结果表明，机器人在模拟时间13.1 s前处于角加速状态，13.1s后处于角减速状态.

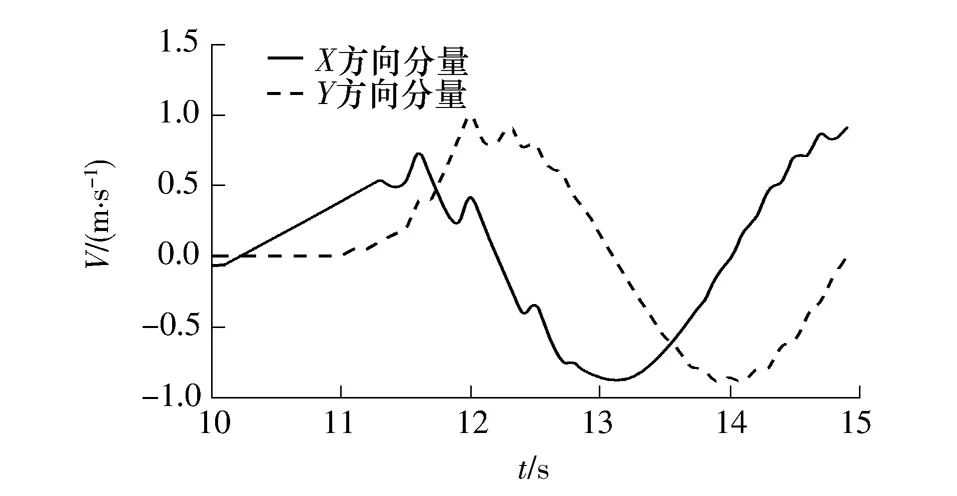
图6 绝对坐标系下速度分量的时间历程Fig.6 Time histories of linear velocity components in inertial frame

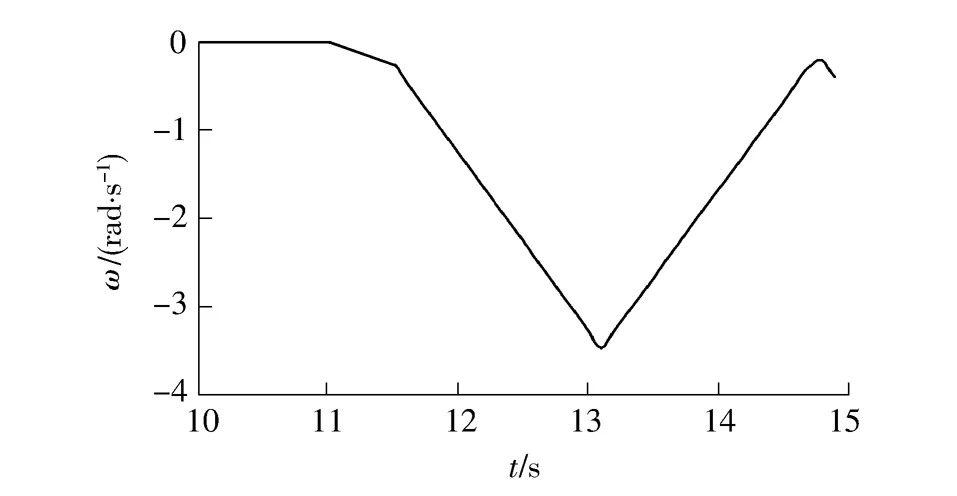
图7 绝对坐标系下角速度的时间历程Fig.7 Time history of yaw in inertial frame

在控制过程中脐带缆与机器人连接点处所受的张力、控制螺旋桨在绝对坐标系中X、Y方向上所发出的推进力以及机器人主体在运动过程中所受的水动力分量如图8－10所示.

图8 脐带缆下端张力Fig.8 Tension at lower end of the cable

图9 绝对坐标系下推进力各分量的时间历程Fig.9 Time histories of propulsion components in inertial frame

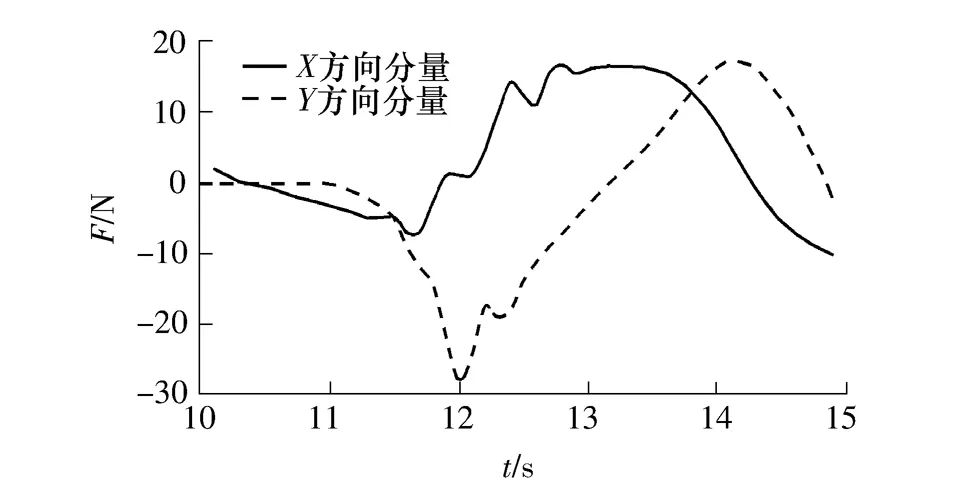
图10 机器人主体所受水动力在绝对坐标系下的分量Fig.10 Hydrodynamic loading on the robot presented in inertial frame

从图8的结果可以知道，由于脐带缆长度与轨圆直径之比相对较大，在整个控制作业中机器人脐带缆所受的张力变化很小，其值大致等于机器人主体在水中的重量.从这一现象可以推断，在控制水下机器人沿文中所描述的圆形轨迹运动的过程中，脐带缆的力学作用主要体现在抵消机器人的重量、维持其在水下一定的深度方面，而对机器人回转运动状态起主导作用的是控制螺旋桨所发出的推进力.将图9与6的结果进行对比不难发现:控制螺旋桨所发出的推进力在绝对坐标中的分量与机器人速度分量的变化趋势相似，这也进一步证实了螺旋桨推进力对机器人回转运动所起的主导作用.将图10的结果与图9比较可以看出:机器人主体在运动过程中所受的水动力变化趋势大致与螺旋桨推进力的变化趋势相反，这说明在绝对坐标的平面上螺旋桨推进力与机器人主体的水动力大致组成了一对相位相反的平衡力系.同时，由图10可见，在模拟时间为13.1 s左右时，机器人主体所受的水动力达到了最大值.这是由于此时机器人处于点{X，Y}={－0.75m，1m}附近的位置(见表2)，这时候来流方向与机器人的运动方向相反，因此其水动力值达到了最大值;而当模拟时间达到14.9 s左右时，机器人处于点{X，Y}={－0.75m，0m}附近的位置，此时来流方向与机器人的运动方向一致，因此其水动力达到了最小值.

在控制过程中绝对坐标系下的控制螺旋桨所发出的推进力力矩、机器人主体在运动过程中所受的水动力力矩以及它们所合成的合力矩的数值模拟结果如图11所示.

从图11中可以看出，推进力力矩和合力矩的变化趋势与图7所示的艏向角变化趋势相一致.这说明:控制螺旋桨所发出的推进力力矩的转向性质决定了机器人所受的合成力矩的转向性质，推进力力矩对水下机器人的转向运动起主导作用.

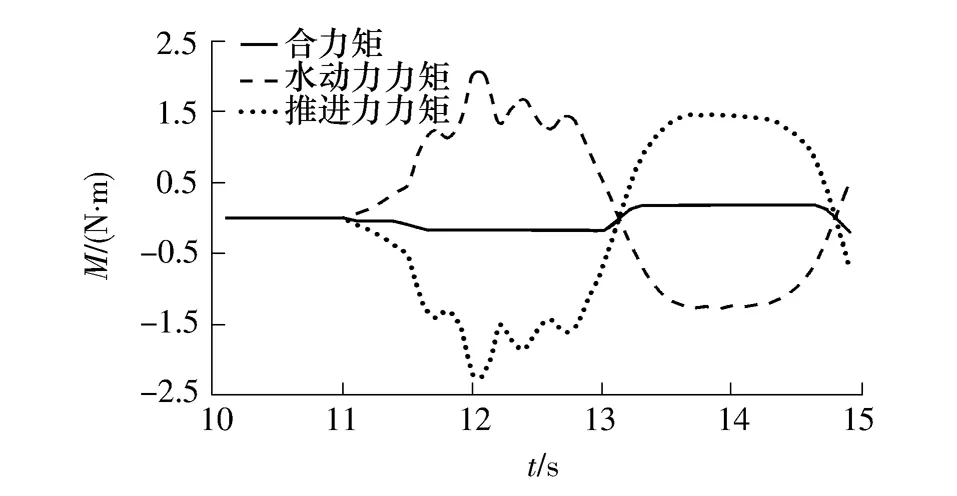
图11 作用在机器人主体上的力矩Fig.11 Moments exerted on main body of the robot

控制过程中在机器人局部坐标系下的螺旋桨推进力的时间历程如图12所示，采用2.3节介绍的方法进行推力分配和换算之后，各螺旋桨转速ω'的时间历程如图13所示.

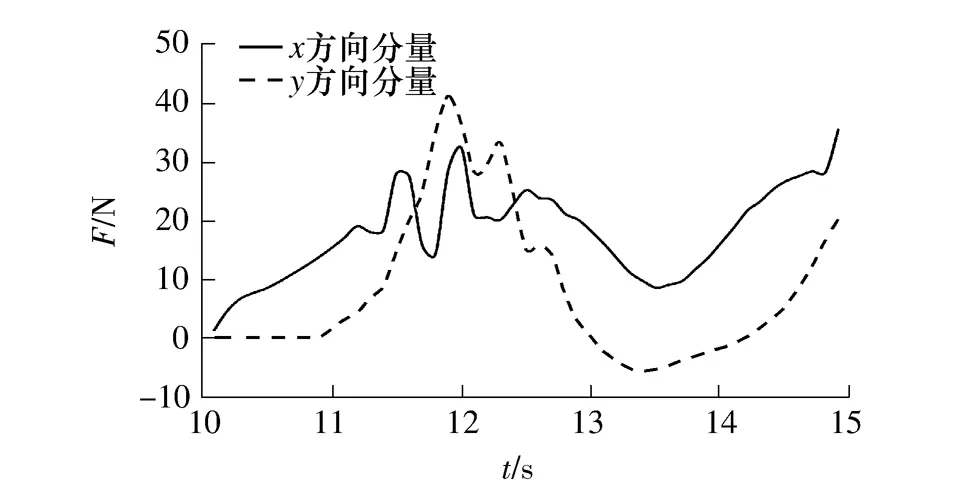
图12 局部坐标系下推进力分量的时间历程Fig.12 Time histories of propulsion components in local frame

图13 导管螺旋桨转速的时间历程Fig.13 Time histories of rotating speed of propellers

对比图12和13的结果可以看出:螺旋桨推进力在机器人局部坐标系下的x方向分量的变化方式与3、4号螺旋桨转速的变化方式一致;y方向的分量则与1、2号螺旋桨一致.这一现象说明推进力在x、y方向的分量与这两组螺旋桨转速的性质直接相关.实际上，根据图1的螺旋桨布置方式以及文中所设定的机器人在轨圆运动中的控制目标，结合图13所给出的各个螺旋桨的转速特征，不难发现，控制机器人在轨圆上作回转运动时，3、4号螺旋桨所发出的推进力主要是用于推动机器人沿着轨圆的轨迹运动，它们所发出的推力(或转速)几乎相等，这一对螺旋桨对机器人不产生回转力矩;而1、2号螺旋桨的作用是保证机器人在运动过程中其艏向角与轨圆相切，正是由于1、2号螺旋桨所发出的推进力的差值构成了控制机器人艏向角变化的回转力矩.

5 结语

文中在已建立的完整带缆遥控水下机器人水动力数学模型的基础上，引入由模糊神经算法构建的控制器，对多自由度上的轨迹和姿态进行同步控制.利用所设计的控制器，可以通过调节螺旋桨的转速使其发出适当的推进力，进而达到操纵水下机器人沿指定轨迹与姿态运动的目的.采用文中所提出的方法，可以以数值模拟的方式观察带缆遥控水下机器人在控制操纵过程中的水动力与控制数值信息，这些信息包括:水下机器人的轨迹与姿态、作用在水下机器人主体上的水动力载荷、为操纵机器人沿特定的轨迹与姿态运动而由控制螺旋桨所发出的转速及推进力、脐带缆的动力学特征等.

所采用的带缆遥控水下机器人系统综合考虑了机器人、脐带缆、控制螺旋桨的动力贡献后，以完全耦合的方式建立统一的水动力数学模型，在此基础上加入水下机器人的控制系统，从整体、耦合的观点去分析带缆遥控水下机器人在控制操纵过程中的动力特性.这一模型克服了现有的带缆遥控潜器系统水动力数学模型将系统各组成部分割裂处理，未能从系统整体理论框架中去观察脐带缆、水下机器人、控制螺旋桨等耦合作用的缺陷，因而可以更加客观地分析水下机器人的控制与水动力机理.

［1］ Driscoll F R，Lueck R G，Nahon M.Development and validation of a lumped-mass dynamics model of a deep-sea ROV system ［J］.Ocean Research，2000，22:169-182.

［2］ Ming-Chung Fang，Chang-Shang Hou，Jhih-Hong Luo.On the motions of the underwater remotely operated vehicle with the umbilical cable effect［J］.Ocean Engineering，2007，34:1275-1289.

［3］ 朱克强，李维杨.带缆遥控水下机器人空间运动仿真［J］.中国造船，1996(3):96-104.Zhu Ke-qiang，Li Wei-yang.Simulation of space motion for tethered remotely operated vehicle［J］.Shipbuilding of China，1996(3):96-104.

［4］ 吴家鸣，郁苗，朱琳琳.带缆遥控水下机器人水动力数学模型及其回转运动分析［J］.船舶力学，2011，15(8):827-843.Wu Jia-ming，Yu Miao，Zhu Lin-lin.A hydrodynamic model for a tethered underwater robot and dynamic analysis of the robot in turning motion［J］.Journal of Ship Mechanics，2011，15(8):827-843.

［5］ 朱琳琳.带缆遥控水下机器人水动力数学模型的研究［D］.广州:华南理工大学土木与交通学院，2009:8-20.

［6］ Ablow C M，Schechter S.Numerical simulation of undersea cable dynamics ［J］.Ocean Engineering，1983，10(6):443-457.

［7］ Gertler M，Hagen G L.Standard equations of motion for submarine simulation［R］.Washington:Technical Report DTMB 2510，David Taylor Research Center，1967.

［8］ 赖华威，刘月琴，吴家鸣.基于CFD方法的螺旋桨性能计算与分析［J］.船海工程，2009，38(4):131-135.Lai Hua-wei，Liu Yue-qin，Wu Jia-ming.Calculation and analysis of propeller performance by CFD ［J］.Ship and Ocean Engineering，2009，38(4):131-135.

［9］ Wu J M，Lai H W，Zhu L S.A practical numerical method to forecast the hydrodynamic behavior of a ducted thruster in the flow field of a tethered underwater robot［C］∥Proc of the 19th Int Offshore and Polar Eng Conf.Osaka:The International Society of Offshore and Polar Engineers(ISOPE)，2009:710-715.

［10］ Wu J M，Yu M，Zhu L H.Trajectory and attitude control of a tethered underwater robot［C］∥Proc of the 20th Int Offshore and Polar Eng Conf.Beijing:The International Society of Offshore and Polar Engineers(ISOPE)，2010:287-294.

［11］ 刘曙光，魏俊民，竺志超.模糊控制技术［M］.北京:中国纺织出版社，2001:205-212.

［12］ 甘永.水下机器人运动控制系统体系结构的研究［D］.哈尔滨:哈尔滨工程大学船舶工程学院，2007:64-65.