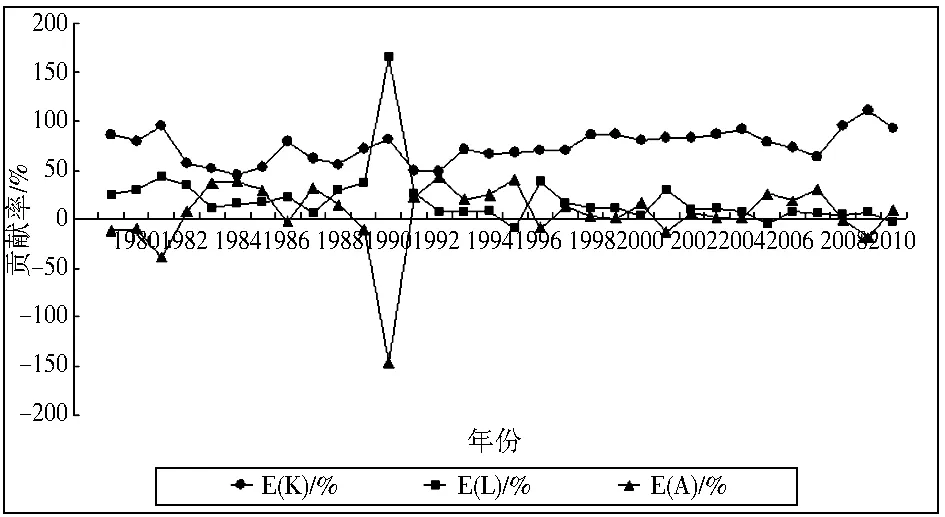
科技、资本、劳动的贡献率比较
——基于中国改革开放30年数据
2012-01-24王文寅张叶峰
王文寅,张叶峰
(1.中北大学 经济与管理学院,山西 太原 030051;2.烟台南山学院 经济与管理学院,山东 烟台 265706)
一、引言
改革开放以来,我国科技事业迅速发展,科技进步对经济增长和社会进步的作用日益彰显。有关这方面的研究成果已经不少,本文则以改革开放以来我国科技进步贡献的阶段性数量特征为主线,研究资本、劳动、科技对经济增长的贡献率,从中可进一步显示科技进步与经济增长关系在不同时期的特征,同时可以观察国际金融危机背景下我国扩大内需中科技进步的“异动”情况。
二、所谓“资本挤出科技,科技挤出劳动”的假设
静态上,在资源总量一定和技术不变的条件下,资本、劳动、科技三大要素的份额及它们对经济增长的贡献率是彼此消长的。而在动态上,在近代以来的世界各国经济增长过程中,科技贡献率越来越大,其次是资本贡献率,而劳动贡献率相对地越来越小,这应该是经济发展的一般规律。在这一总的趋势下,特别是在某些特殊时期,往往是资本贡献率大了,科技贡献率就降低;科技贡献率大了,劳动贡献率就降低,呈现出所谓“资本挤出科技,科技挤出劳动”的要素贡献互相消长的现象。这既是经济一般规律的反映,也是三大要素在经济增长中的双重对立统一关系的反映。
三、模型、指标和数据
(一)模型简介
本文运用广义C-D生产函数的组合模型来研究我国科技进步对经济增长的贡献。传统C-D生产函数的主要自变量只有劳动和资本,随着科技进步在经济增长中的作用日益显著,生产函数得到进一步扩展,容纳了科技进步因素。如果样本为时间序列数据,则有广义生产函数:
Y=A0eγ tKαLβ.
(1)
其中,Y为可能的最大产出,K、L分别为生产过程投入的资本和劳动,α为资金投入弹性系数,β为劳动投入弹性系数;A0为基期技术水平,t为时间变量,γ为技术的年平均增长率,A0eγ t反映了技术进步对产出的影响情况,A0、γ为待估参数[1-2]。
(二)指标选取
1.产出指标。本文选用GDP作为衡量我国经济产出量的指标,为排除价格因素的影响,使时间序列具有纵向可比性,需要把以当年价格计算的GDP转化为以不变价格计算的GDP。为此,产出指标用以1978年为基期折算得出不变价格的GDP作为统计分析的数据,具体的折算公式如下:

2.资本投入指标。理论上,资本投入量是指每年的资本使用流量,但是每年的资本使用流量在现实生活中很难计量,所以只能将资本使用流量用资本存量来代替。目前国际上较为通行的测算资本存量的方法是由戈德史密斯(Goldsmith)在1951年提出的永续盘存法(PIM),随后乔根森(Jorgenson)等经济学家对之进行了完善,OECD定期公布的10个成员国的资本存量数据都是用永续盘存法估算的。为了测算精确,本文也用永续盘存法对资本存量进行测算,其假定前提是相对效率采取几何递减的模式,此时重置率为常数,用模型表示为:
Kt=(1-δt)Kt-1+It.
(2)
其中,Kt为t期资本存量,Kt-1为t-1期资本存量,δt为t期资本折旧率,It为t期的投资额。
3.劳动投入指标。本文借鉴新经济增长理论的观点,劳动投入指标选用人力资本来度量。人力资本的度量方法,从产出角度用劳动报酬法,从投入角度用学历指数法、技术等级或职称等级法、教育成本法、人力与非技术劳动分解法和受教育年限法。考虑到指标度量的简易性、数据的可得性和精确性、方法的简明性等要求,本文选用受教育年限来度量人力资本。受教育年限的公式可以表示为:
ht=16×n1+12×n2+9×n3+6×n4+2×n5.
(3)
其中,ht为t年的平均受教育年限,即人力资本水平;nt表示各教育层次人口的比重。
(三)数据来源
本文的产出(GDP)、资本(K)、劳动(L)的样本数据取自我国1978-2010年的年度数据,资料来源为中国统计年鉴2011和新中国六十年汇编。1982年、1987年、1990年、1995-2010年的各学历层次劳动力人数数据可查,其他年份数据通过插值法计算可得,样本数据共33个。
四、模型的建立、估计及参数的检验
(一)模型建立
对广义C-D生产函数两边取对数可得:
lnGDP=lnA0+γ×t+α×ln(K)+β×lnL+μ1
(4)
根据数据,用Eviews6.0软件对(4)式进行最小二乘法估计,估计的模型为:
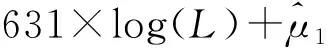
(t值) (-1.808 654) (-0.917 909)
(3.818 007) (3.246 978)
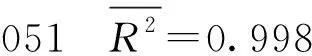
当模型的拟合优度(R2)很高,F值很高,而每个回归参数估计值的方差Var (βj)又非常大(即t值很低)时,说明解释变量间可能存在多重共线性[3]。以上的估计符合这种情况,并且C值、T值的t检验没通过,因此解释变量LNL和LNK间可能存在多重共线性。下面做LNL和LNK的相关系数矩阵来检验是否存在多重共线性(见表1)。

表1 LNK和LNL的相关系数矩阵
通过检验发现解释变量LNL和LNK之间的相关系数达到了0.953 616,可以判断存在严重共线性,因此需要修正模型来消除多重共线性。
(二)模型修正
在规模报酬不变即α+β=1的状态下,可通过人均GDP和人均资本(即GDP/L和K/L)来消除多重共线性。对所考察的具体问题能否施加约束条件,或者说能否直接对施加约束后的模型进行回归,还需进行相应的检验。在Eviews6.0软件中,通常用沃尔德(Wald)检验[4]。Wald检验可以判断拟合结果是否满足系数约束条件,即检验是否满足-1+C(3)+C(4)=0。通过Wald检验来进行对数的约束性检验(见表2),检验的零假设为:
C(3)+C(4)=1.
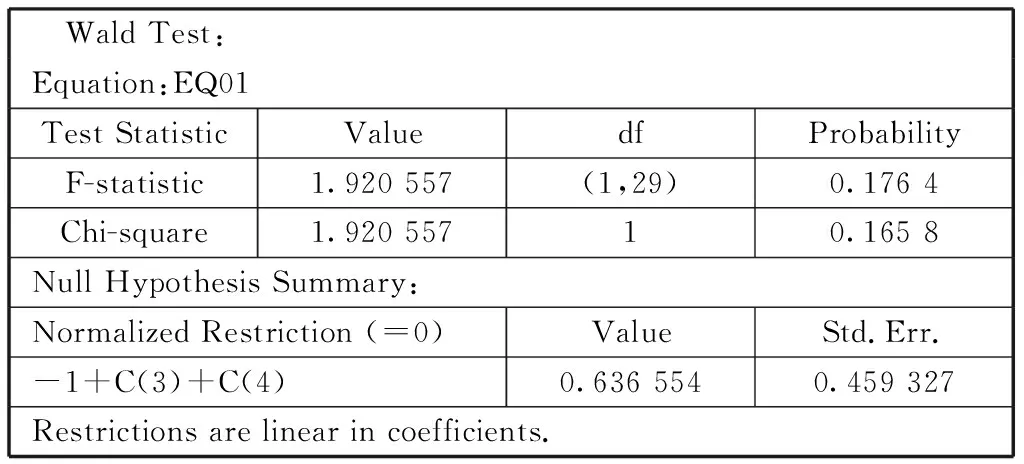
表2 Wald检验的输出结果
由表2可知检验的P值是0.176 4,大于a=0.05的显著性水平,所以接受原假设,即满足系数约束条件,可以认为在-1+C(3)+C(4)=0的约束下的受约束回归模型与原模型具有相同的解释力,因此消除了多重共线性,则可建立如下模型:
ln(GDP/L)=lnA0+γ×t+α×ln(K/L)+μ2.
(5)
根据数据,利用Eviews6.0软件进行最小二乘法估计可得到如下的估计方程:
log(GDP/L)=-2.008 299+0.015 928×t+
(t值) (-16.688 76)(7.048 468)
(18.266 16)
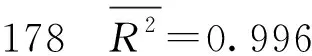
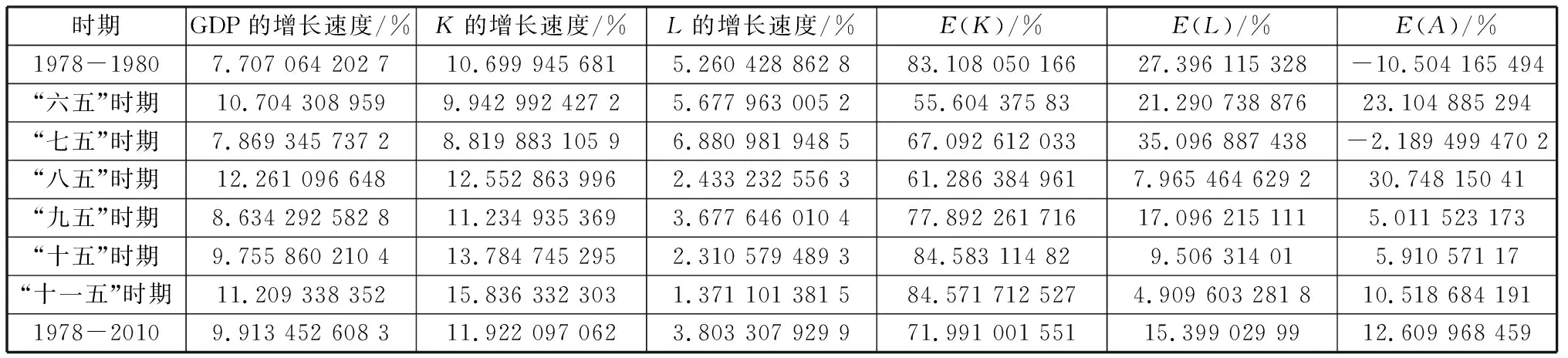
经检验在a=0.05显著水平下F检验通过,说明模型整体显著成立,R2=0.997 178,表明模型拟合度较好,但是D.W值太低仅为0.647 130,根据0 对模型的一阶、二阶自相关的分别检验,根据LM乘法判断,得表3和表4所示的结果,由伴随概率可知,模型存在一阶、二阶自相关,则可建立以下的修正模型: ln(GDP/L)=lnA0+γ×t+α×ln(K/L)+AR(1)+AR(2)+μ3. (6) 表3 LM的检验结果 表4 LM的检验结果 因此可以利用Eviews6.0软件,用广义差分估计模型,估计结果如下: (t值) (-8.944 960) (3.315 794) (11.355 65) (6.177 369) (-3.013 223) 根据LM乘数检验法判断,得表5和表6所示的结果,由此可知其模型已经不存在一阶和二阶自相关。 表5 LM的检验结果 表6 LM的检验结果 经检验在a=0.05显著水平下C值、T值和LOG(K/L)的t检验全部显著通过;R2=0.998 815,说明回归方程对样本数据拟合的较好,各解释变量和被解释变量之间是高度线性相关的;F检验显著通过且比以前提高了;由怀特(white)检验即表7可知,nr2=21.235 19,它对应的P值为0.095 8,大于0.05,则可判定模型不存在异方差性,因此可以说模型通过了计量经济学检验。 表7 White检验结果 由以上结果可知,α=0.598 619,β=0.401 381,γ=0.013 564.因此模型标准为: GDP=0.152 715e0.013 564tK0.598 619L0.401 381. (7) 其中,α=0.598 619,说明当资本投入增长1%,可以导致其GDP增长0.598 619%;β=0.401 381,说明劳动投入增长1%,可以导致其GDP增长0.401 381%;γ=0.013 564,说明我国的技术进步的年增长率是1.356 4%. 资本投入、劳动投入和科技进步贡献率的计算公式分别为: E(A)=1-E(K)-E(L). 由表8可知,1978-2010年我国的经济平均增长速度为9.91%,将近10%,并且1978-2010年对经济增长的推动数资本贡献率最大,为71.99%,劳动的贡献次之,为15.39%,科技进步的贡献最低,为12.61%.资本投入的平均增长速度为11.92%,虽然有一定的波动,但是总体上表现出上升的势头,而且超过了产出的增长速度,尤其在“十一五”时期资本投入的增长速度是15.84%,但其贡献率是84.57%,说明我国的经济尚未改变主要靠资本投入的传统粗放式增长方式。劳动投入的增长差不多是一路向下的趋势,“十五”时期和“十一五”时期的增长速度不够1%,导致劳动投入的贡献也一路下滑,也不足10%,远低于产出的增长速度。这主要是由于近年来中国高新技术的迅猛发展,使得许多传统型工人纷纷下岗,说明中国高素质的人才匮乏,需要尽快提高劳动人员的素质。“九五”时期和“十五”时期科技进步对中国经济增长的贡献大体在5%,“十一五”时期科技进步对中国经济增长的贡献增长到10.52%,但这与发达国家相比还有很大的差距,说明中国的科技进步对经济的贡献还有很大的提升空间。需要说明的是,本文的科技进步是狭义的科技进步,即主要着眼于R&D投入,若从广义科技进步(包括了制度、管理、教育等的创新)来测算,那么科技进步贡献率要高得多,达到40%左右。 表8 1978-2010年科技、资本、劳动的贡献率 应当指出,测算的时期越长,原始数据的局部异常变化对计算结果的影响就越小,其测算结果的变化也趋稳定和一致。 由图1中可看出,资本投入一直是我国经济增长的主要因素,同时科技进步的作用也逐步增强,资本投入和科技进步对我国经济增长的贡献发生着此起彼伏的变化。 图1 我国各要素贡献率 那么,怎么理解2007-2010年的科技进步贡献率的下降呢?众所周知,受2007年美国的次贷危机影响,世界经济一直在衰退中徘徊,迫使各国政府纷纷救市。我国救市的方案就是注入资本,靠资本拉动内需,因此从2007-2010年我国资本的投入急剧增长,导致科技进步的贡献率相应下降成负值。更深层次的原因还在于:在扩大内需中,一些地方和部门还不同程度地存在着科技进步仅仅是经济增长手段的不正确观念,以及由此产生的科技和经济“两张皮”的做法,这显然不利于建立“依靠”和“面向”相统一的科技发展机制(即“经济建设要依靠科学技术,科学技术要面向经济建设”)。而劳动投入的贡献率在最近几年稍微有点下降,则说明就业人数增长缓慢。其原因有二:一是我国经济增长逐步脱离高位态势;二是科技进步相对地减少了对劳动的有效需求。 因此,我国在未来的发展中,应适当地减少要素投入量,协调要素投入的比例,提高要素生产率。尤其是资本投入要尽可能倾向于科技事业,即加大所谓“科技的资本投入”,其中主要是科技R&D投入,还要继续大力发展教育,提升劳动者的素质,扩大人力资本的流量和存量。 参考文献: [1] Charles W,Cobb and Paul H,Douglas.A Theory of Production[J].American Economic Review,1928,18(1):61-94. [2] [美]道格拉斯·C·诺斯.经济史上的结构与变革[M].励以平,译.北京:商务印书馆,1999:3-45. [3] 攸 频,张晓峒.Eviews6.0实用教程[M].北京:中国财政经济出版社,2008:163. [4] 孙敬水.计量经济学学习指导与Eviews应用指南[M].北京:清华大学出版社,2010:51.(三)模型的再修正


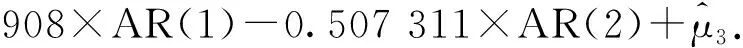
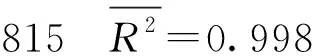



五、各要素的测算及分析
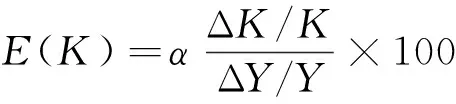
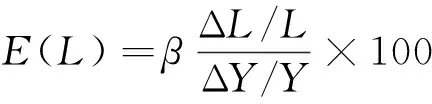
六、验证和结论