基于灰色马尔可夫组合模型的福州港吞吐量预测
2012-01-24高玲
高 玲
(福州大学 八方物流学院,福建 福州 350116)
灰色系统理论是我国学者邓聚龙在1982年提出的一种主要研究“贫信息、小样本”不确定系统的理论方法,是一种具有不确定性的内部因素关系且部分信息未知、部分信息已知的系统[1]。它的基本思路是将系统中观测到的数据序列按照某种规则,通过累加生成新的序列来降低系统的灰度,进而找出系统潜藏的有序规律来构建模型[2]。
马尔可夫链是20世纪初俄国数学家马尔可夫发现的一种系统状态转移规律,系统数据列的无后效性是它最显著的特点。这里的“无后效性”即指在一个系统数据列的随机过程x(t),当t=t0时刻状态已知,此后t0的状态与t0以前状态无关,只与t0时的状态有关[3]。马尔可夫模型预测法就是利用马尔可夫链的“无后效性”这一特性,通过原始数据序列求得序列的状态转移矩阵,然后再根据状态转移矩阵来估计随机事件未来的发展趋势及可能出现的结果。
目前,关于港口货物吞吐量的预测大多使用灰色系统理论来进行预测,如,王冠威、王纯提出了利用多变量灰色系统预测模型GM(1,N)来预测港口的集装箱业务量[4];周强采用趋势外推法、专家法、多因素动态生成系数法、综合配流法和灰色预测法这五种方法进行组合来预测天津港铁路的集装箱吞吐量、海铁联运量,进而探讨天津港的发展前景[5];林珊仟、陈燕琴通过运用多变量灰色系统预测模型GM(1,N)预测厦门港集装箱海铁联运的生成量[6];陈燕琴基于海铁联运运量数据的小样本性、不确定性特征,把灰色理论GM(1,1)模型与BP神经网络模型相结合,预测厦门港集装箱海铁联运运量[7];孙国卿利用多变量灰色系统预测模型预测大陆桥运输量,并通过与其他联运方式比较海铁联运的效率和成本,来探讨海铁联运的效益问题与运量问题[8];黄民生运用灰色关联法对福建港口物流影响因素进行关联度分析[9]。
灰色系统理论虽然运用广泛,但是单一模型的运用存在一定的局限性,当碰到波动的数据,数据列会出现拟合度差,预测精度不高的现象。有鉴于此,本文针对港口吞吐量相关数据的不确定性、小样本性、波动性等特征,提出了灰色马尔可夫组合预测模型。灰色马尔可夫组合预测法克服了单一模型的局限性,既从小样本、不确定的数据序列中寻找出数据的演变规律,又通过状态转移矩阵来修正波动下的数据,两种方法有机的结合,对预测福州港的货物吞吐量具有严密的科学性和现实参考价值。
一、灰色马尔可夫组合模型的建立
灰色马尔可夫组合模型充分利用灰色系统理论与马尔可夫模型的信息和优点,大幅提高预测结果的精确度,其具体步骤如下。
1.根据原始数据列X(0)进行数据累加,生产新的数据列X(1)。
2.建立GM(1,1)的基本形式:
x(0)(k)+az(1)(k)=b.
(1)
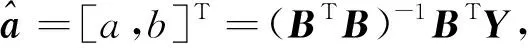
4.确定GM(1,1)模型的白化方程,并累加还原求得灰色预测公式:
(2)
5.利用所求预测公式,分别求出不同时刻的模拟数据。
6.利用残差相对值检验所求预测值的误差,δ(k)为残差,ε(k)为残差相对值,利用δ(k)及ε(k)检验模拟数据,ε(k)越小表明精度越高。其中,
(3)
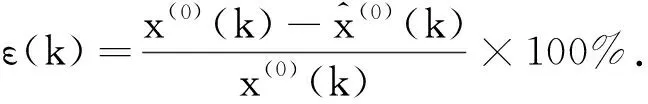
(4)
7.根据不同年份数据的偏差规律来划分状态。其中,状态划分的数量不仅跟拟合数据的误差有关,还与样本数据相联系。状态划分的数量越多就需要较多的样本数据,若划分数量较少,状态差别就会不明显,失去了对波动的调整。根据预测数据的误差范围确定状态空间,然后根据需要将灰色模型拟合的观测值进行状态划分,一般分为3~5个状态,如果波动性越大,就需要划分越多的状态。
8.根据样本资料,计算出状态间转移的频率并利用概率来估计、构造状态转移矩阵。其中,
k步转移矩阵概率为:
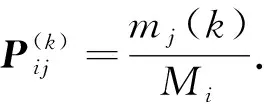
(5)
一步转移矩阵概率为:
(6)
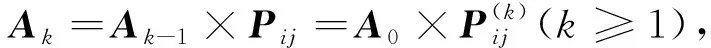
10.计算预测值。马尔可夫预测只能给出一个具体的灰色范围,即状态概率范围,对于短期的预测有唯一最大概率值是可取的,但在最大值不唯一时,往往会产生较大的误差。本文就考虑用期望值EAk作为未来k时刻的预测值,即
EAk=M(k)×Ak×B.
(7)
其中M(k)为k未来时刻利用灰色模型预测的结果,B为状态转移矩阵Pij的评价权值,即
B=(b1b2…bn)T.
(8)
11.利用期望值计算预测值,即为运用灰色马尔可夫组合模型预测。
二、福州港吞吐量的灰色模型预测
福州港作为福建省的重要港口,随着海峡两岸经济贸易关系的深入,基础设施的不断完善,福州港迎来了难得的发展机遇。本文选取2000-2011年福州港货物吞吐量和集装箱吞吐量[10-11]作为原始数据来预测未来5年港口的发展动向,原始数据如表1所示。
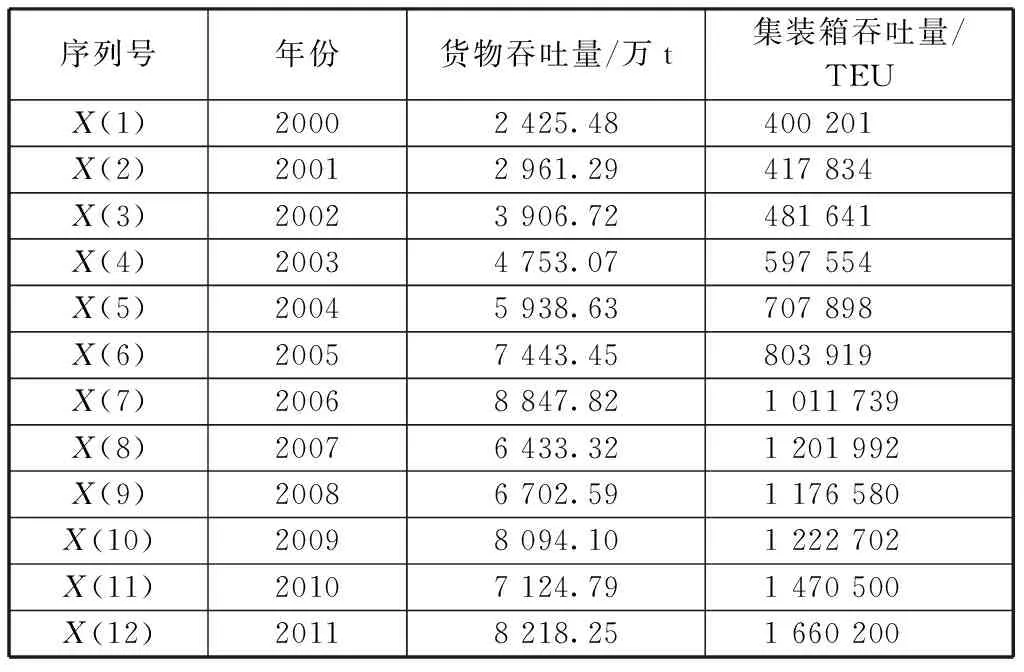
表1 福州港货物吞吐量和集装箱吞吐量原始数据
资料来源:福建省统计年鉴。
以表1中数据作为因子变量,利用公式(1)建立灰色GM(1,1)预测模型,求出货物吞吐量的灰色系数a=-0.063 633,b=4 297.860 869,利用公式(2)得出:
x(t+1)=69 888.462 729exp(0.063 633 6)-67 462.982 729.
集装箱吞吐量的灰色系数a=-0.123 785,b=411 472.109 201,利用公式(2)得出:
x(t+1)=3 741 819.942 711 exp (0.123 785t)-3 324 086.942 711.
采用DPS数据处理软件分别求得未来5年(2012-2016年)货物吞吐量及集装箱吞吐量预测值如表2所示。
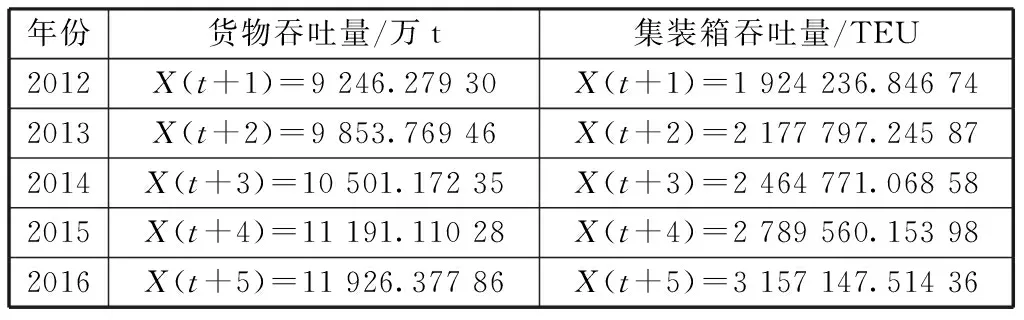
表2 未来5年福州港货物及集装箱吞吐量预测值
利用公式(3)和公式(4)对初始数据进行残差模型检验,数据如表3和表4所示,以反证表2预测值的精确度。
一般情况下,拟合值的残差相对值越低,该灰色预测模型的应用就越精确,若平均误差和相对误差的绝对值都小于10%,则认为误差水平可以接受。根据表3的结果可知,每个阶段的残差相对值相对过大,12个残差相对值中小于10%的只有6个,误差比率高达50%;又如表4中各阶段的残差相对值相对过大,误差水平小于10%的有8个,误差比率超过30%.因此可以判定采用灰色GM(1,1)单一模型预测福州港货物和集装箱的吞吐量误差较大,结果比较粗糙,表2中的预测值不稳定。有鉴于此,下文使用马尔可夫模型修正。
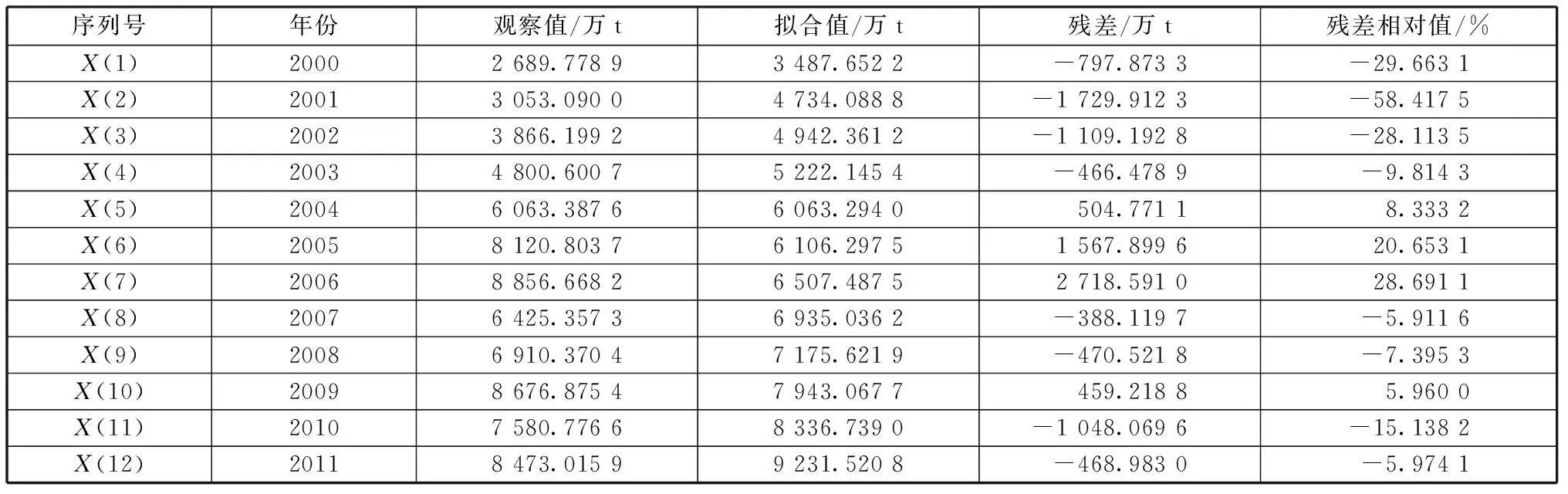
表3 福州港货物吞吐量的拟合值及误差
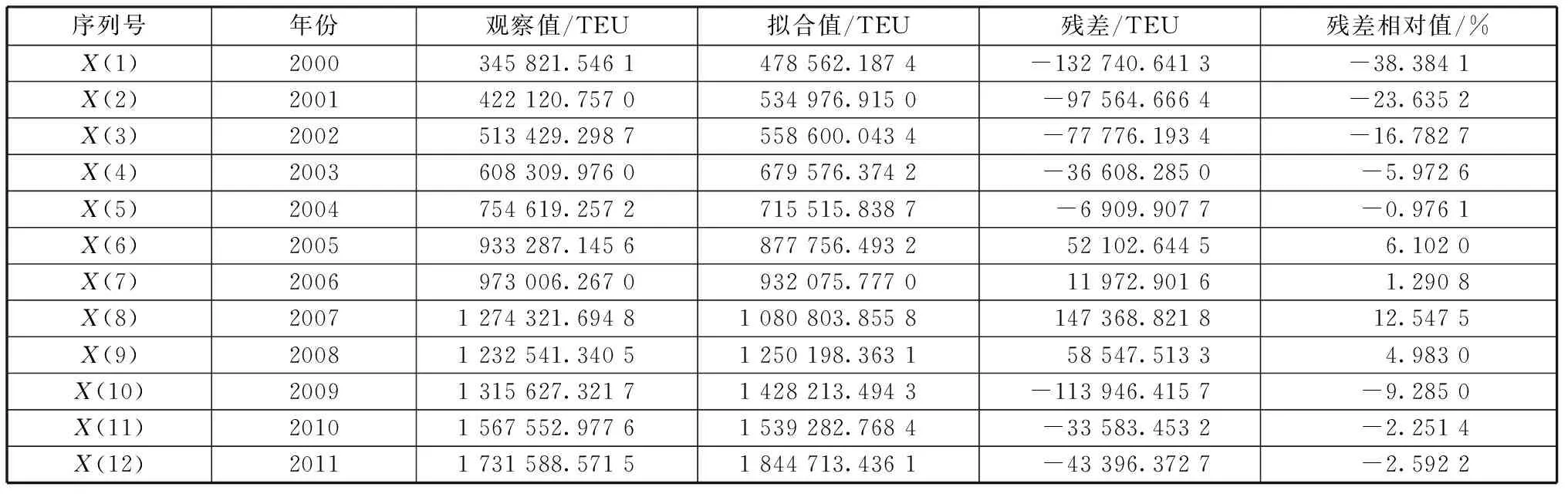
表4 福州港集装箱吞吐量的拟合值及误差
三、马尔可夫模型修正
根据马尔可夫模型的应用经验及实际值与预测值之间的误差相对百分比(残差相对值)将误差状态划分为以下3种,如表5 所示。

表5 误差状态划分
货物吞吐量P1及集装箱吞吐量P2的状态转移矩阵分别为:
货物吞吐量的状态E1、E2、E3观察值/拟合值比值的分布如下:
E1:0.64~0.91,
E2:0.92~1.13,
E3:1.33~1.23.
集装箱吞吐量的状态E1、E2、E3观察值/拟合值比值的分布如下:
E1:0.79~0.92,
E2:0.90~1.05,
E3:1.18~1.23.
转移矩阵P1、P2的评价权值如下:
B1=(0.78 1.03 1.25)T,
B2=(0.86 0.98 1.18)T.
货物吞吐量及集装箱吞吐量2011年的状态同属E2,即A0=(0 1 0)代表2011年的状态向量。
2012-2016年货物吞吐量状态向量如下:
2012:A1=A0×P1=(0.2 0.6 0.2),
2012-2016年集装箱吞吐量状态向量如下:
2012:A1=A0×P1=(0 0.86 0.14),
根据EAk=M(k)×Ak×B计算货物吞吐量及集装箱吞吐量未来5年的预测值,其中M(k)为k未来时刻利用灰色模型预测的结果,B为状态转移矩阵Pij的评价权值。计算结果如表6所示。
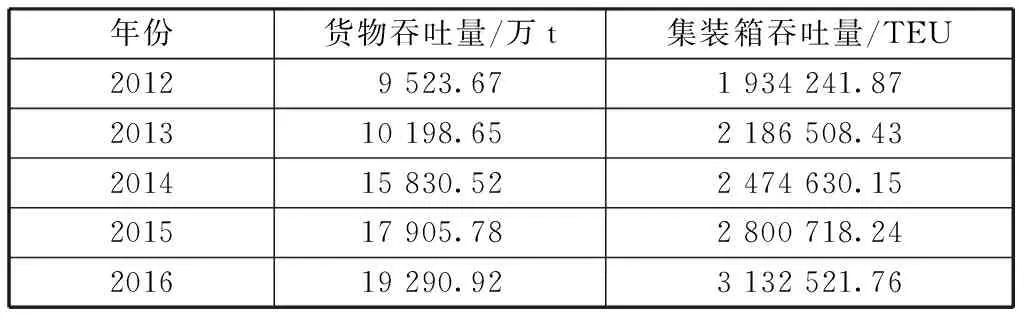
表6 未来5年福州港货物及集装箱吞吐量预测值
四、精度比较分析
同样利用公式(3)和公式(4)对灰色马尔可夫组合模型进行残差模型检验,结果如表7所示,可见运用灰色马尔可夫组合模型预测出福州港的货物吞吐量和集装箱吞吐量的残差相对值都小于10%,相比表3和表4的预测残差值有较高的精确度。同理可证,表6的预测值要比表2的预测值具有较高的可信度。
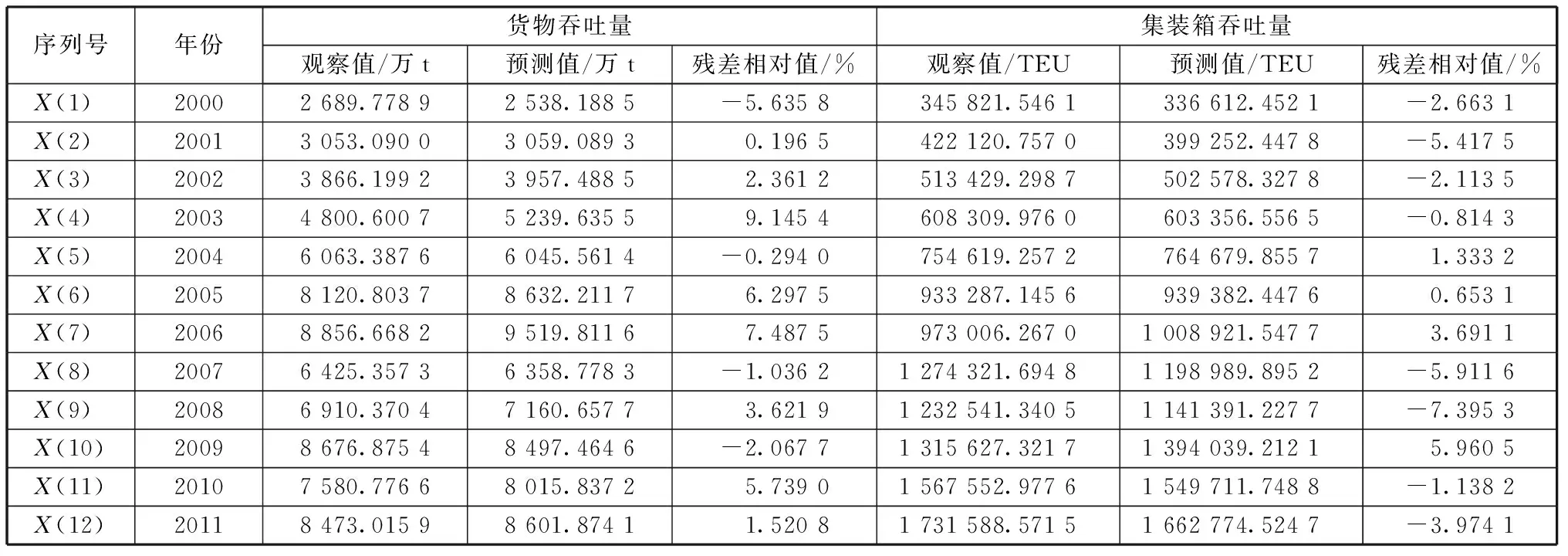
表7 福州港货物及集装箱吞吐量预测
五、结论
本文采用灰色预测和马尔可夫链相结合的组合预测方法预测福州港未来5年的货物走向趋势,并验证模型的拟合程度。算例表明,通过组合预测进行加权组合,相对单一灰色预测法,灰色马尔可夫组合模型预测精度高,符合事物的发展规律,同时避免过拟合问题,提高了模型的推广能力,为港口业界提供了新的预测模型,具有积极的现实意义。
参考文献:
[1] 刘思锋,党耀国,方志耕,等.灰色系统理论及其应用[M].北京:科学出版社,2010:147-160.
[2] 邓聚龙.灰色系统基本方法[M].武汉:华中科技大学出版社,2005:68-85.
[3] 李维铮,郭耀煌,甘应爱,等.运筹学[M].北京:清华大学出版社,2005:191-210.
[4] 王冠威,王 纯.基于灰色系统理论的集装箱海铁联运量预测[J].集装箱化,2008(5):20-22.
[5] 周 强.天津铁路集装箱海铁多式联运问题研究[D].天津:河北工业大学,2008:34-40.
[6] 林珊仟,陈燕琴.厦门港集装箱海铁联运量预测[J].集装箱化,2010(5):31-33.
[7] 陈燕琴.基于灰色理论和BP网络的集装箱海铁联运量预测[J].中国水运,2010,10(12):75-76.
[8] 孙国卿.海铁联运运量预测与效益研究[D].大连:大连海事大学,2010:37-43.
[9] 黄民生.海峡西岸港口物流对接模型研究[M].北京:科学出版社,2009:36-46.
[10] 福建省统计局.福建统计年鉴[M].北京:中国统计出版社,2011:226-230.
[11] 中华人民共和国交通运输部.中国港口年鉴[M].上海:中国港口杂志社,2011:167.
