物体从球面顶点下滑问题的研究
2012-01-23刘梅
刘梅
(安徽师范大学物理与电子信息学院 安徽 芜湖 241000)
杨玉超
(安徽省淮南市第十三中学 安徽 淮南 232072)
冯霞
(安徽师范大学物理与电子信息学院 安徽 芜湖 241000)
在物理教学中,常见到质点自光滑球面顶端滑下的理想问题.对于物体与球面间有摩擦的实际问题,如何分析?有什么规律?本文将采用量纲分析、全微分积分法进行研究,并分析质点自光滑球面顶端滑下的理想问题的几种情况.
1 “物体从球面顶点下滑” 的一般问题
【例1】如图1所示,一个质量为m的物块,在重力作用下自一半径为r的固定球面的最高点无初速度滑下.若质点与球面间的摩擦因数为μ,求质点离
开球面时,它与球心的连线和竖直方向夹角θ所满足的关系?

图1
解析:(1)量纲分析法
质点下滑过程中,假定θ与质量m,半径r,重力加速度g,摩擦因数μ有关,即
θ=f(m,r,g,μ)
因为θ是一个无量纲的量,无法把四个量有机结合形成一个无量纲的量,因此θ与μ一个参量有关,即
θ=f(μ)
(2)全微分积分法
物体下滑过程中,在球面上受重力、支持力和摩擦力,由于其速率逐渐增加,所以支持力逐渐减小直到脱离球面时减小到零.由牛顿第二定律得
法向方程

(1)
由动能定理

(2)
消去N得
dv2-2(μv2+grsinθ-μgrcosθ)dθ=0
(3)
式(3)不是全微分方程.把式(3)记为
P(v2,θ)=1
Q(v2,θ)=-2(μv2+grsinθ-μgrcosθ)

设有f(θ)形式的积分因子
以f(θ)乘式(3)两端,得全微分方程
e-2μθdv2-2e-2μθ(μv2+grsinθ-μgrcosθ)dθ=0
(4)
e-2μθdv2-2e-2μθμv2dθ-2e-2μθgrsinθdθ+
2e-2μθμgrcosθdθ=0
d(e-2μθv2)-2e-2μθgrsinθdθ+2e-2μθμgrcosθdθ=0
对上式积分,得方程的通解为
(5)
且当t=0时,将θ=0,v=0代入上式,可得
(6)
所求方程的通解为

(7)
质点离开球面时,N=0,由式(1)得
v2=grcosθ
将上式 代入式(7)得
e-2μθ(3cosθ+6μsinθ)=2(1-2μ2)
(8)
即θ所满足的关系
3cosθ+6μsinθ=2(1-2μ2)e2μθ
(9)
式(9)符合量纲分析得到的结论即θ只与μ有关.
讨论:若质点与球面间无摩擦μ=0时得
e2μθ=1
(10)
3cosθ=2
(11)
即θ所满足的关系
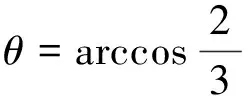
(12)
2 物体从球面顶点下滑的理想化问题
【例2】小物体自半径为R的光滑球面顶点从静止开始下滑,求:
(1)物体脱离球面时它与球心的连线与竖直方向夹角θ;
(2)小物体落到地面时的速度v.
解析:小物体自光滑球面顶点从静止开始下滑,从运动学角度看,物体先做圆周运动,脱离后做抛体运动.从动力学角度看,物体在球面上受重力和支持力,物体下滑过程中,由于其速率逐渐增加,所以支持力逐渐减小直到脱离球面减小到零.小物体即将脱离球面的条件是N=0.
解法一:(1)小物体自光滑球面顶点从静止开始下滑,到即将脱离球面,支持力不做功,只有重力做功,机械能守恒.以球面顶点为势能零点,设物体即将脱离球面的速度为v1,则
(13)
由牛顿第二定律,得

(14)
物体脱离球面条件
N=0
(15)
解得
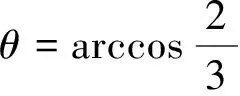
(16)
(2)设小物体落到地面时的速度为v,由机械能守恒得
解得

(17)
物体脱离后做抛体运动,水平方向分速度不变
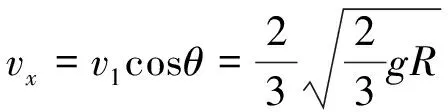
(18)
设小物体落地时速度与水平方向的夹角为α,所以

(19)

(20)
解法二:对于球面上运动的质点,运动轨迹的切线方向上有
(21)
法线方向上有

(22)
由式(21)得
其中,s为运动路程,亦即半圆柱周围弧长.即
vdv=gsinθds
又因为Rdθ=ds,即
vdv=gsinθRdθ
(23)
设质点刚离开圆柱面时速度为v,离开点与竖直方向夹角为θ,对式(23)两边积分,得

(24)
刚离开圆柱面时N=0 即
(25)
联立式(24) 、(25) 得
【例3】如图2所示,在光滑水平面上放置一半径为R、质量为M的光滑半球.质量为m的小滑块自球面顶部由静止开始受微小扰动下滑,求:当m=M时,滑块滑至何处(θ为多少)时脱离球面?

图2
解析:滑块脱离半球的瞬间,相对球面的速度为u,沿球面切向;半球对地速度为v,滑块脱离半球后,半球速度不变.
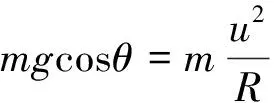
(26)
以半球、滑块为系统,水平方向不受外力,动量守恒,则
m(ucosθ-v)-Mv=0
(27)
由系统机械能守恒

(28)
由式(26)~(28)得
cos3θ-6cosθ+4=0
(29)

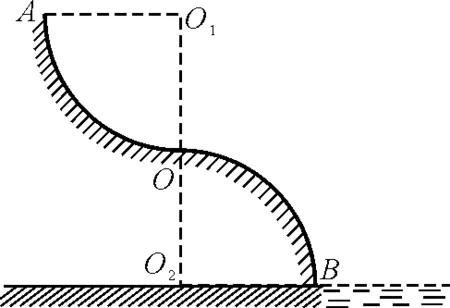
图3


(2)凡能在O点脱离滑道的小滑块,其落水点到O2的距离为多大?
