探究单摆加速度与摆角的关系
2012-01-23刘权
刘权
(苏州市陆慕高级中学 江苏 苏州 215131)
1 建立单摆模型
如图1(a)所示,小球质量为m,绳长为L,单摆的摆角为α,将小球在A位置静止释放.

图1
2 理论推导
设某时刻单摆的位置如图1(b),此时单摆的偏角为θ,小球的速度为v,小球的加速度为a,则有
(1)
(2)
(3)
联立(1)、(2)、(3)三式,得
a2=4g2(cosθ-cosα)2+g2sin2θ
将上面表达式做无量纲处理,得

(4)
3 绘图

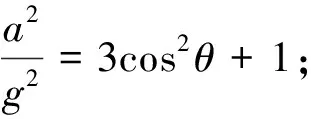


结果如图2所示.

图2
结论:从以上三种情况看,单摆加速度大小变化与摆角α有关.选取单摆从最低点θ=0到最高点θ=α的运动过程,将单摆加速度大小变化分为三类.
类型一:单摆加速度大小不断增加 (摆角α=30°时情况);
类型二:单摆加速度大小先减小后增大(摆角α=60°的情况);
类型三:单摆加速度大小不断减小 (摆角α=90°的情况).
4 定量分析
对表达式(4)进行处理,得
(5)
(1)当α=90°时, 单摆的偏角θ从零增加到α时,根据表达式(5)可以看出单摆加速度大小变化属于类型三(单摆加速度不断减小).


5 图像分析
根据上述定量分析知道:α=41.41°是临界角.


图3
图4是对图3在0°≤θ≤4.2°范围内的图像做了放大处理.

图4



图5
图6是对图5在0°≤θ≤10°范围内的图像做了放大处理.

图6
从图5和图6中发现单摆的加速度在0°≤θ≤41.4°的范围内的确是不断增加的.
6 最值讨论
(1)当α=90°时,单摆在最低点(θ=0°)加速度最大,在最高点(θ=α)加速度最小.
(2)当0<α≤41.41°时,单摆在最低点加速度最小,在最高点时加速度最大.
(3)当41.41°<α<90°时,讨论单摆加速度的最值情况.
2)单摆加速度最大值要么在最低点θ=0°,要么在最高点θ=α.
根据表达式(5),设单摆在最低点和最高点加速度相等,


根据表达式(5)得知:
当41.41°<α<53.13°时,单摆在最高点加速度最大.
当53.13°<α<90°时,单摆在最低点加速度最大.
