从三个层次突破高考最后一题

沈荣灿 王国军

（上虞中学 浙江 绍兴 312300）

带电粒子在磁场中的运动是历年高考考查的重点，各地高考往往将它作为压卷题，具有较高的区分度．由于在平时学习中学生没有及时、有效地归纳，临场找不到恰当的解题方法而心生畏惧，加之在两个半小时内要完成物理、化学、生物三门学科组成的理综考试，时间显得尤为紧迫．如何在短时间内迅速找到突破口一直是困扰广大师生的难题．本文从三个层次分析带电粒子在磁场中运动题型，并给出相应对策，以期对学生、教师有所帮助．

1 基础题

【例1】一匀强磁场，磁场方向垂直于x Oy平面，在x Oy平面上，磁场分布在以O为中心的一个圆形区域内．一个质量为m、电荷量为＋q的带电粒子，由原点O开始运动，初速为v，方向沿x正方向．后来，粒子经过y轴上的P点，此时速度方向与y轴的夹角为30°，P到O的距离为L，如图1所示．不计重力的影响．求磁场的磁感强度B的大小和x Oy平面上磁场区域的半径R．

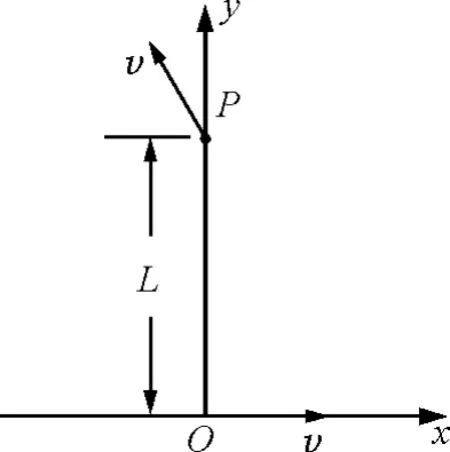
图1

对策：熟练掌握解题的基本思路，提高画图能力．

（1）找圆心，画轨迹 ——确定圆心的几种方法

方法一：已知入射方向和出射方向时，可以通过入射点和出射点分别作垂直于入射方向和出射方向的直线，两直线的交点就是圆弧轨道的圆心，如图2（a）所示；

方法二：已知入射方向和入射点、出射点的位置，可以通过入射点作入射方向的垂线，连接入射点和出射点，做其垂线，这两条垂线的交点就是圆弧轨道的圆心，如图2（b）所示．

（2）由几何关系求半径——弦切角、圆心角、速度偏向角之间的关系，如图2（c）所示．

弦切角θ、速度偏转角α、圆心角β，三者关系

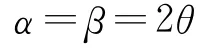
（3）确定圆心角求时间

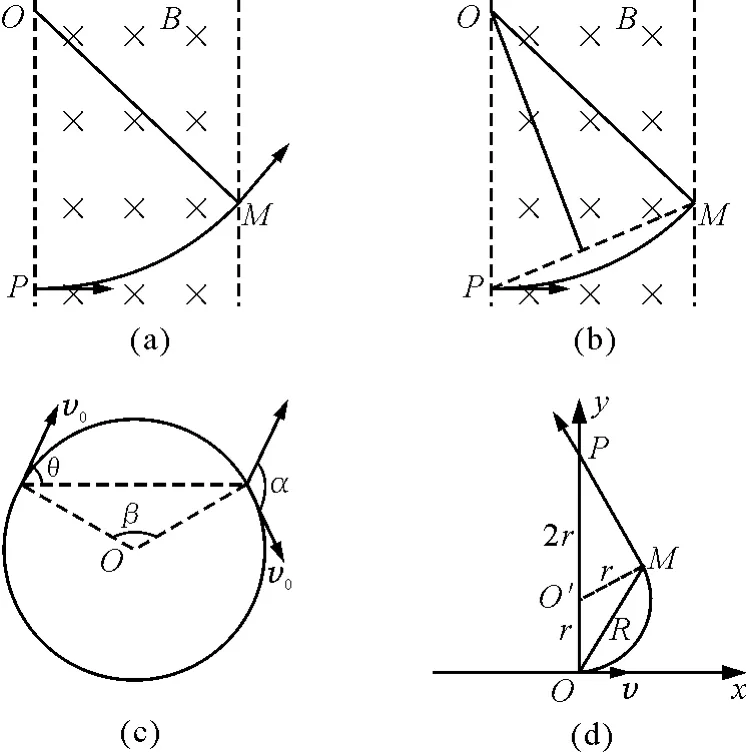
图2

解：已知条件中给出了入射点、入射方向和出射方向，需要找到出射点．引出射方向的反向延长线，再作反向延长线的垂直，该垂线被截得线段＝O′O，则M点为出射点，O′点为圆弧轨道中心．画出带电粒子轨迹如图2（d）所示．

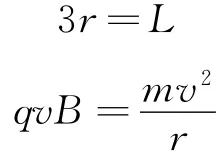
2 提高题

【例2】（2010年高考全国卷第26题）如图3所示，在0≤x≤槡3 a区域内存在与x Oy平面垂直的匀强磁场，磁感应强度的大小为B．在t＝0时刻，一位于坐标原点的粒子源在x Oy平面内发射出大量同种带电粒子，所有粒子的初速度大小相同，方向与y轴正方向的夹角分布在0～180°范围内．已知沿y轴正方向发射的粒子在t＝t0时刻刚好从磁场边界上P（槡3 a，a）点离开磁场．求：

（2）此时刻仍在磁场中的粒子的初速度方向与y轴正方向夹角的取值范围；

（3）从粒子发射到全部粒子离开磁场所用的时间．

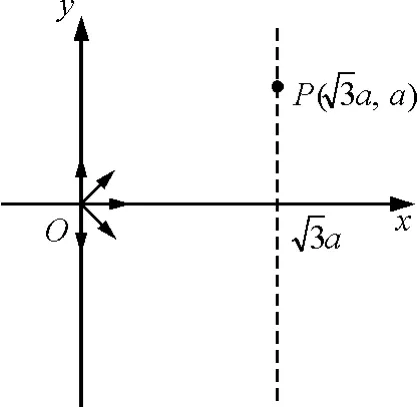
图3

此类题型的特点是带点粒子从同一点以相同速度大小、不同速度方向或相同速度方向、不同速度大小射入磁场，要求学生画出动态圆，寻找临界条件．但正如图4所示，要求学生在短时间画出动态圆，并分析出临界条件，对学生的画图、分析能力要求较高．

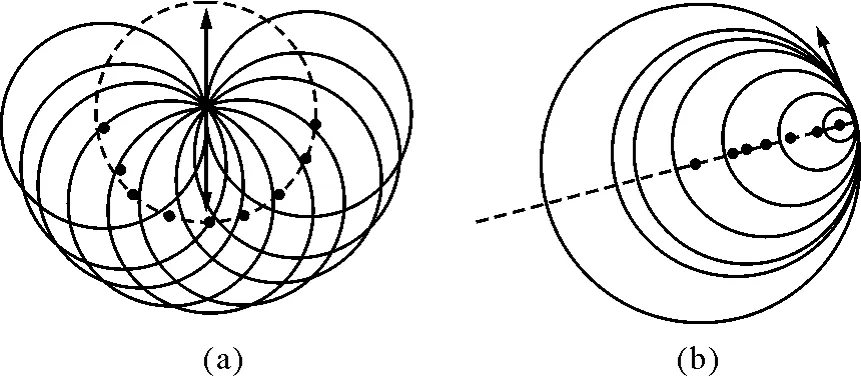
图4

对策：化动态圆为动态弦，从弦长角度分析临界条件．

对第一类动态圆，若粒子轨迹为劣弧，则相同弦长对应相同弧长、相同弦切角、相同运动时间等；较长弦对应较长弧、较大弦切角、较长运动时间等．

解：（1）、（3）略．

（2）由题知，沿＋y方向射入磁场的粒子，OP为其轨迹圆弧的弦，对应的弦切角为60°，若粒子入射速度方向顺时针旋转，如图5所示，则粒子在右边界的出射点P将向下移动，弦长OP先变短后变长，即对应粒子在磁场中运动的时间先变短后变大．

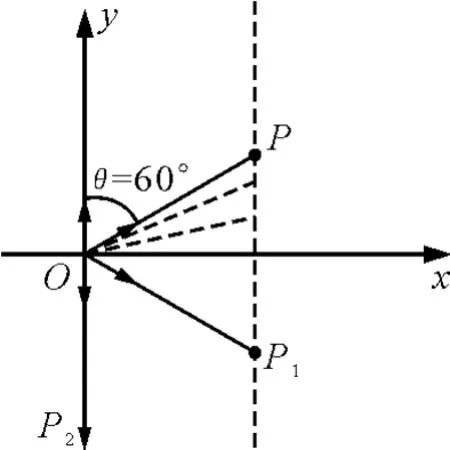
图5

如图，当弦OP1与OP关于x轴对称，该粒子在磁场中运动时间t＝t0，此时弦切角同为60°，速度与＋y成60°角．

同理分析可知，粒子从左边界射出的临界弦OP2，该粒子的速度方向与＋y成120°角．

3 能力提升

【例3】（2009年高考浙江卷第25题）如图6所示，x轴正方向水平向右，y轴正方向竖直向上．在x Oy平面内有与y轴平行的匀强电场，在半径为R的圆内还有与x Oy平面垂直的匀强磁场．在圆的左边放置一带电微粒发射装置，它沿x轴正方向发射出一束具有相同质量m、电荷量q（q＞0）和初速度v的带电微粒．发射时，这束带电微粒分布在0＜y＜2R的区间内．已知重力加速度大小为g．

图6

（1）从A点射出的带电微粒平行于x轴从C点进入磁场区域，并从坐标原点O沿y轴负方向离开，求电场强度和磁感应强度的大小和方向．

（2）请指出这束带电微粒与x轴相交的区域，并说明理由．

此类题型较新颖，对学生运用数学工具解决物理问题的能力要求较高．

对策：运用数学工具——平面几何、解析几何、参数方程．

（1）平面几何．添加相关辅助线，寻找直角三角形或菱形，通过三角函数或勾股定理确定长度关系；

（2）解析几何．写出磁场边界方程（约束方程）与粒子运动的轨迹方程，联立方程组解出入射点和出射点坐标；

（3）参数方程．以变量为参数，写出边界点与参数的关系，消参写出轨迹方程．

解：（1）略；

（2）

方法一：解析几何

从任意一点P水平进入磁场的带电微粒在磁场中做半径为R的匀速圆周运动．如图7所示，连接PO′点与y轴的夹角为θ，P点的坐标为（－R sinθ，R＋R cosθ），轨迹圆心Q的坐标为（－R sinθ，R cosθ）．

图7

圆周运动轨迹方程为

而磁场边界方程为

x2＋（y－R）2＝R2

第一组解（0，0）即为出射点坐标，第二组解［－R sinθ，R（1＋cosθ）］即为入射点P的坐标．由此可知带点粒子均从原点O点射出．

方法二：平面几何

过P点做PQ⊥v，且PQ＝R，连接PO′和Q O．

由PQ瓛O′Q，可推得四边形PO′OQ 为平行四边形．

由PQ＝PO′＝R，可推得平行四边形PO′OQ为菱形，则有Q O＝R．

以Q为圆心，R为半径做圆弧．可知，P点射入的粒子将从原点O射出．

从上例不难发现，平面几何方法解题的特点是简洁、易懂、计算量小，但对分析、推理能力要求较高，具有一定技巧性．一般学生遇到此类问题感觉棘手，难以寻找题目的切入点；而运用解析几何方法按部就班，通过轨迹方程与约束方程确定交点坐标，寻找规律，学生易下手，找到题目的突破口，但往往需要解方程组，计算量相对较大．

【例4】如图8所示，直角坐标系中直线AB与x轴夹角∠BAO＝30°，AO长为a．假设在点A处有一放射源可沿∠BAO所夹范围内的各个方向放射出质量为m、速度大小均为v、电荷量为e的电子，电子重力忽略不计．在三角形ABO内有垂直纸面向里的匀强磁场，当电子从顶点A沿AB方向射入磁场时，电子恰好从O点射出．试求：

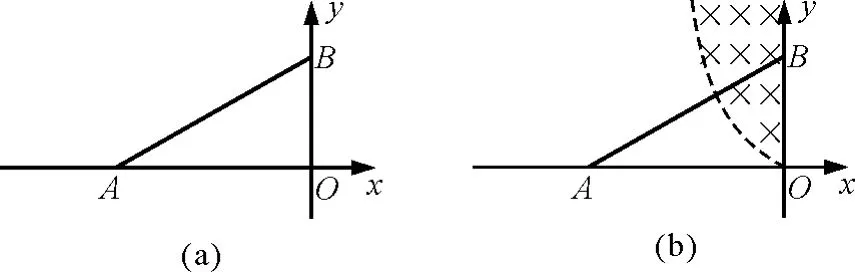
图8

（1）从顶点A沿AB方向射入的电子在磁场中的运动时间t；

（2）磁场大小、方向保持不变，改变匀强磁场分布区域，使磁场存在于三角形ABO内的左侧，要使放射出的电子穿过磁场后都垂直穿过y轴后向右运动，试求匀强磁场区域分布的最小面积S；

（3）磁场大小、方向保持不变，现改变匀强磁场分布区域，使磁场存在于y轴与虚线之间，示意图见图8（b）所示，仍使放射出的电子最后都垂直穿过y轴后向右运动，试确定匀强磁场左侧边界虚线的曲线方程．

解：（1）略；

（2）当电子沿AB方向射入磁场，其圆弧部分轨迹即为有界磁场的上边界（半径为a，圆心角为60°的圆弧）．

设电子以与x轴夹θ角射入磁场，离开磁场P点的坐标为（x，y），如图9（a）所示．

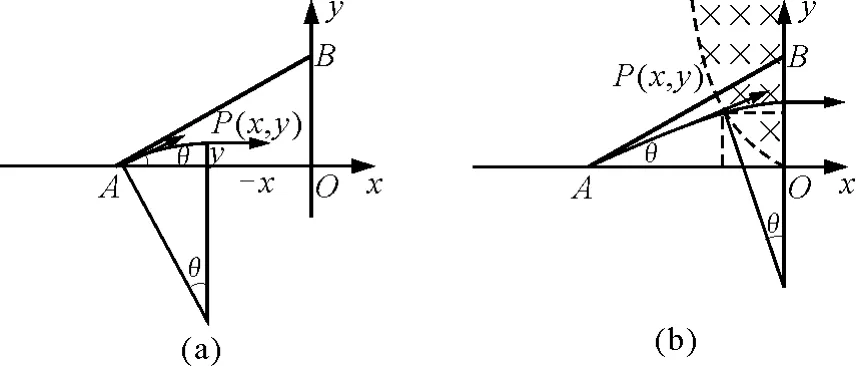
图9

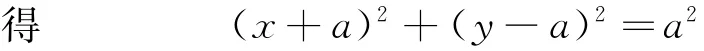
磁场的下边界为以（－a，a）为圆心，a为半径的部分圆弧，磁场区域分布的最小面积为

（3）设电子与x轴正方向夹角θ，从P（x，y）点进入磁场，如图9（b）所示．

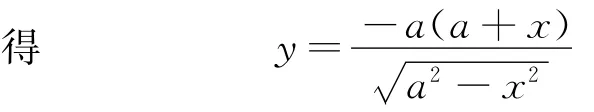
【例5】如图10所示，以O为原点建立平面直角坐标系xy，沿y轴放置一平面荧光屏．在y＞0，0＜x＜0．5 m的区域有垂直于纸面向里的匀强磁场，磁场的磁感应强度大小B＝0．5 T．在原点O放一个开有小孔粒子源，粒子源能同时放出比荷为＝4．0×105C／kg的不同速率正离子束，沿与x轴成30°角从小孔射入磁场，最后打在荧光屏上，使荧光屏发亮．入射正离子束的速率在零到最大值vm＝2．0×106m／s的范围内，不计离子之间的相互作用，也不计离子的重力．

（1）求离子打到荧光屏上的范围；

（2）若在某时刻（设为t＝0时刻）沿与x轴成30°角入射的各种速率的正离子，求经过10－7s时这些离子所在位置构成的曲线方程．

图10

解：（1）略；

如图11所示，设离子粒子轨道半径为r，t时刻所在位置P点坐标为（x，y）．

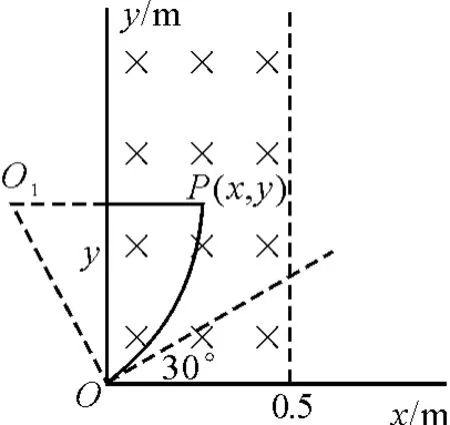
图11

由图可知

运用参数方程解决粒子轨迹方程或磁场的边界方程的难点在于如何设置参数，从例5、例6不难发现——设变化的物理量为参数．例5中速度大小确定，方向可变，故需设入射角θ为参数；例6中速度偏转角确定，但速度大小连续变化，故设半径r为参数．