我国省域科技创新人才队伍建设的现状评价与空间集聚效应研究＊——基于GPCA模型和ESDA方法

丁 刚，罗 暖

（福州大学公共管理学院，福建福州350108）

区域科技创新人才队伍建设对区域创新能力的增强乃至社会经济的发展都产生着重要影响。目前，关于科技人才队伍建设现状评价的相关研究普遍采用以下几种方法：一是层次分析法和模糊综合评判法相结合，一般的研究路径是先通过Delphi法征询专家意见进而确定指标体系，之后采用层次分析法确定各级指标权重，最后应用模糊综合评判法建立评价模型。如，曹文瑞即采用这一研究路径对医学类科技人才进行了评价[1]；王宇婷对区域科技人才开发水平的评价亦是采用层次分析法和模糊综合评判法相结合的方法[2]。二是数据包络分析（DEA）法，即在构建评价指标体系的基础上运用DEA方法对人才建设进行评价。如，高真真应用数据包络分析法对全国31个省（市）区以及河南省17个市的科技人才投入产出效率进行评价分析[3]；刘保民亦是采用DEA方法对河南省科技人才投入产出效率进行综合评价[4]。三是灰色关联分析（GRA）法，主要是通过对反映因素之间发展趋势相似或相异程度的“灰色关联度”指标的计算评价区域科技人才的建设现状。如，何荣旺等将由灰色关联分析得出的关联度作为确定各类科技人才对河南省发展贡献率的依据，从而进行科技人才资源的优化配置[5]；沈春光等人在整理分析影响区域科技人才创新能力的各种因素的基础上，基于多层次评价指标体系，运用灰色系统理论探讨了区域科技人才的创新能力等[6]。

然而，就上述各种方法在现有研究中的应用而言，仍存在以下不足之处。第一，层次分析法采用主观赋权方式，易使评价指标体系的科学性及评价结果的客观性受到影响；第二，数据包络分析（DEA）法虽然简单且不受函数形式限制，但其权系数的选择往往过于极端，难以实现对决策单元的有效排序；第三，灰色关联分析（GRA）方法是衡量因素间关联程度的一种方法，对各样本采用平权处理，客观性较差。

基于上述考虑，本研究拟采用以全局性和客观赋权为特征的全局主成分分析GPCA（Gener－alization Principal Components Analysis）模型，在综合评价指标体系的基础上，对全国30个省（市）区2006－2009年科技创新人才队伍建设的现状进行动态综合评价。按照Anselin[7]空间计量经济学的观点，在空间单元上存在的某一属性值或产生的某种社会经济现象与邻近地区同一属性值或现象是有联系的，大部分空间数据具有空间自相关性或空间依赖性的特征，而在空间自相关性的影响下，易导致空间集聚现象的产生。可见，我国各省域的科技创新人才队伍建设之间亦可能存在空间相关性和一定程度的空间集聚现象。为更全面地对我国省域科技创新人才队伍建设现状的空间演化格局和集聚态势有所了解，本研究还拟采用探索性空间数据分析（Exploratory Spatial Data Analysis，ESDA）方法，该方法可有效测度现象或事物之间的空间关联程度，就研究对象在空间集聚形态的演化过程进行探讨分析，以期对提升区域科技创新人才队伍建设水平的长效机制的构建有所裨益。

一、省域科技创新人才队伍建设水平评价

（一）指标体系框架

基于区域科技创新人才队伍建设水平指标体系设计的客观性、全面性和科学性等原则，并且参考已有专家、学者的研究成果，笔者拟从人才投入、人才产出、创新环境等三个层面入手，对我国区域科技创新人才队伍建设现状进行综合评价。见表1。

表1 我国区域科技创新人才评价指标体系基本框架

（二）评价过程简介

本研究运用GPCA模型，基于多元统计分析软件STATA 12，对我国30个省（市）区2006－2009年关于科技创新人才队伍建设水平的统计数据进行解析。由于数据获取的原因，样本空间不包括西藏和港澳台地区。本研究全部数据均由《中国统计年鉴》、《中国科技统计年鉴》（2007，2008，2009，2010年）的相关数据进行整理、计算获取，将由15项指标构成的数据集依时间排列，构成全局样本数据表。笔者采用GPCA模型的依据在于：如果分别对2006－2009年期间关于我国区域科技创新人才队伍建设现状历年的数据表分别采用经典主成分分析，将导致其产生迥异的主超平面，这样就难以保证最终评价结果的完整性和科学性。在这种情况下，就需要建立一个简洁且具一致性的子空间，以使历年数据表在该空间上的投影均得到相近似表达，并且从全局视角看，该空间的评价效果是最理想的，综上所述构建起GPCA模型。对于GPCA模型的构建原理和实现步骤，现有文献已作了详细介绍[8]，限于篇幅本研究不再赘述。利用多元统计软件，对我国省域科技创新人才队伍在2006－2009年期间的建设现状进行评价，见表2。

表2 GPCA方法的实施步骤

利用STATA12软件在对数据进行标准化的基础上进行变量间偏相关性的KMO（Kaiser－Meyer－Olkin）检验，结果显示，KMO的数值为0．7286（一般当KMO值大于0．7时，即认为适合做全局主成分分析）。进一步进行Bartlett球形假设检验，结果表明在1%的水平下显著。由此可见本研究选用GPCA方法是合适的。

在对样本数据进行全局主成分分析的过程中，可得到全局主成分的特征值及贡献率，见表3。

表3 全局特征值与贡献率

从表3中可知，前五个全局主成分的方差累计贡献率达到82．04%（高于80%），可见分析效果比较好。本研究确定其为所需提取的五个全局主成分，分别用F1（38．52%）、F2（20．37%）、F3（9．56%）、F4（7．28%）、F5（6．32%）表示，由此得到区域科技创新人才队伍建设水平综合得分F综的评价公式如下：

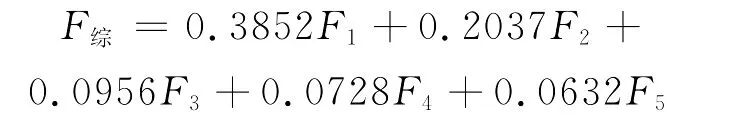
利用综合得分F综的评价公式，可计算出我国省域科技创新人才队伍建设现状的综合得分，见表4。

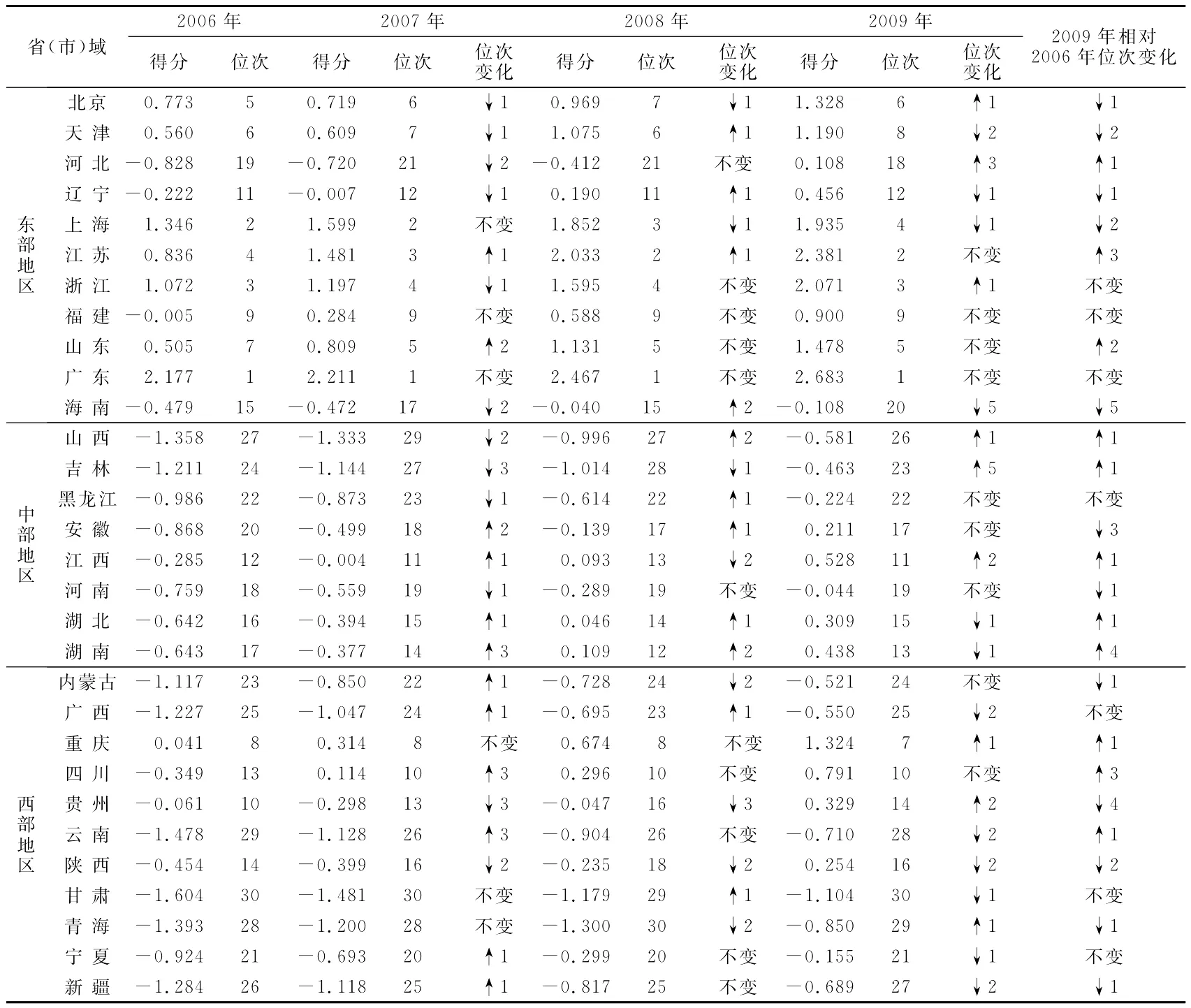
表4 省域科技创新人才队伍建设现状评价

（三）评价结果分析

从表4可以清晰地看出，2006－2009年期间，位于东、中、西三大地带的各省（市）区，其科技创新人才队伍建设现状的综合评价得分均有不同程度的提高，可见我国各省域的科技创新人才队伍建设水平在“十一五”期间内有了一定程度的提升。同2006年相比，2009年在全国范围内排名上升的省域数目，达到了12个，中部地区最多，有5个。湖南和宁夏提升位次最大，均提升了4个位次；江苏和四川次之，均提高了3个位次。排名下降的省域亦达12个，东部占比为5／12，西部占比为5／12。其中海南从2006年的第15位下降至2009年的第20位，下降位次最大；贵州次之，下降了4个位次。综上可知，我国区域科技创新人才队伍建设有了一定程度的改善，且相较于东部地区，中、西部地区的提升更为明显。与2006年相比，2009年东、中、西三大地带得分均值的升幅分别达到37．14%、113．81%和102．18%，中部升幅最高，西部紧随其后，东部升幅最低，从中可以看出在全国范围内各区域科技创新人才队伍建设的发展差距有所缩小，但不均衡态势尚未得到合理改善。

二、区域科技创新人才队伍建设的空间集聚态势分析

我国区域科技创新人才队伍建设水平在评价区间内期初（2006年）和期末（2009年）的空间分布四分位情况显示，分布于不同组别的省域呈现出一定的空间集聚态势。为进一步确定我国区域科技创新人才队伍建设综合得分是否存在显著的空间集聚效应，本研究拟运用ESDA方法，以空间相关性显著检验等达成研究目的。ESDA方法以空间关联测度为核心，由一系列可视化空间数据分析方法与技术集合而成，主要用其来揭示数据的空间异质性和空间依赖性[9]。探索性空间数据分析方法一般分为全域空间关联分析和局域空间关联分析两类。其中，全域空间关联分析主要通过对全局空间自相关统计量的估计，说明现象或事物在空间上的总体关联程度；而局域空间关联分析则依据对局部空间自相关统计量的估计，揭示现象或事物在局域空间上的分布格局与关联程度。见表5。

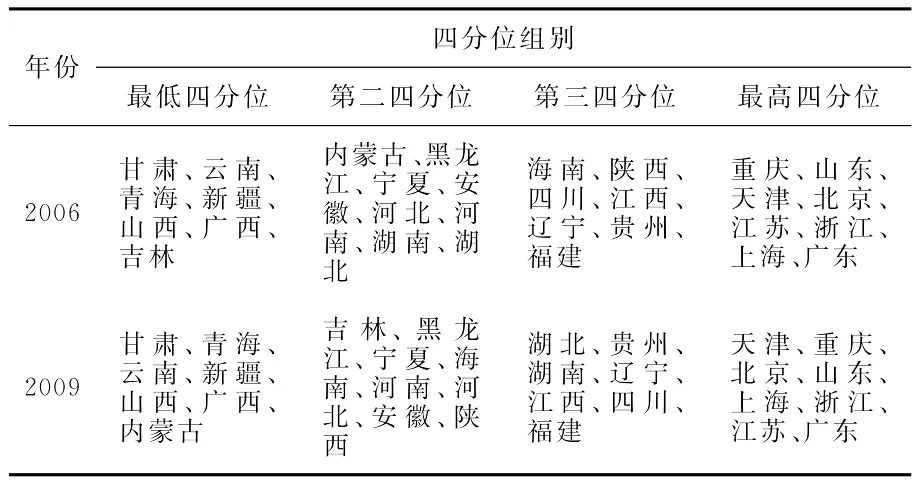
表5 2006年和2009年区域科技创新人才队伍建设综合得分空间分布四分位情况

（一）基于Moran＇s I的全域空间自相关分析

1．Moran＇s I的计算说明。全域Moran指数在1948年由Moran提出，它主要反映的是空间邻接或邻近的单元属性值的相似程度。在有关空间分析的应用研究中经常使用Moran＇s I指数来对全域空间自相关现象的存在与否加以研判说明。Moran＇s I指数计算公式可表示如下：

式（2）中，i＝1，2，…，n；j＝1，2，…，m；m＝n或m≠n。Moran＇s I指数的取值范围为（－1，＋1），可将其看作是各省域观测值的乘积和。当不同区域的科技创新人才队伍建设水平在空间区位上相似时，从全局角度看其空间模式表现出正的空间自相关性；而当邻近省域的科技创新人才队伍建设水平明显地不相似时，就呈现出负的空间自相关性；零空间自相关性指各省域区位数据的分布与其科技创新人才队伍建设水平的空间分布是相互独立的。在Moran＇s I散点图中，可将各地区划分为四个象限的集群模式：图的第一象限，表示科技创新人才队伍建设水平综合得分高的地区被综合得分高的地区所包围（H H）；第二象限，表示科技创新人才队伍建设水平综合得分低的地区被综合得分高的地区所包围（LH）；第三象限，表示科技创新人才队伍建设水平综合得分低的地区被综合得分低的地区所包围（LL）；第四象限，表示科技创新人才队伍建设水平综合得分高的地区被综合得分低的地区所包围（HL）。

2．基于Moran＇s I的检验结果。在得到我国省域科技创新人才队伍建设水平综合得分的基础上，可在随机性假设条件下对其Moran＇s I统计值的显著性进行检验，见表6。

表6 区域科技创新人才队伍建设综合得分的Moran＇s I散点图情况

表6报告了2006－2009年我国30个省（市）自治区科技创新人才队伍建设水平的历年综合得分的Moran＇s I统计分析结果，可以看出，历年的Moran＇s I值分别为0．3435、0．4003、0．4421、0．4453。对上述结果进行显著性检验，发现其正态统计量Z值均高于1．96（正态分布函数在5%水平下的数值），可见各省域间表现出了较为强烈的空间正自相关性。

从表6中，可以发现2006－2009年期间的Moran＇s I散点图的排布均呈现出一定的相似性。2006年的Moran＇s I散点图显示：位于第一象限的省域有北京、上海、天津、江西、福建、浙江、江苏等，其与邻近地区间呈现出正的空间自相关关系（H H）；位于第二象限的省域有安徽、河北、湖南、广西等，其与邻近地区间呈现出负的空间自相关关系（LH）；位于第三象限的省域包括黑龙江、内蒙、新疆、吉林、甘肃、山西、陕西、宁夏、青海、河南、湖北、云南等，其与邻近地区间呈现出正的空间自相关关系（LL）；位于第四象限的省域仅包括辽宁、山东、广东、贵州、重庆、四川等省域，其与邻近地区间呈现出负的空间自相关关系（HL）。相比于2006年，2009年的Moran＇s I散点图显示，分布于不同象限的省域群落构成并无太大变化。根据Rey[9]所提出的时空跃迁测度法，本研究拟对区域科技创新人才队伍建设综合得分的Moran＇s I统计结果的时空演化趋势进行分析。其将时空跃迁形式划分为四种类型：类型Ⅰ描述的是相对位移发生变化的省域跃迁，涵盖HHt→LHt＋1、HLt→LLt＋1、LHt→HHt＋1及等四种形式；类型Ⅱ表示的是有关邻近省域产生的跃迁，涵盖HHt→HLt＋1、HLt→HHt＋1、LHt→LLt＋1、LLt→LHt＋1四种形式；类型Ⅲ标示的是某省域与其邻接省域均都发生了跃迁至其他省域的情形，包括HHt→LLt＋1、HLt→HLt＋1、LHt→HLt＋1、LLt→HHt＋1等四种跃迁形式；类型0标示的是某省域及其邻接省域均维持相同属性的情形，主要有HHt→HHt＋1、HLt→HLt＋1、LHt→LHt＋1、LLt→LLt＋1等四种形式。据此不难发现，2006年至2009年，山东发生了HLt→HHt＋1跃迁，湖北发生了LLt→LHt＋1跃迁，时空跃迁类型均属于类型Ⅱ；贵州发生了HLt→LLt＋1跃迁，时空跃迁类型属于类型Ⅰ；其余27个省域均属于类型0的时空跃迁类型，表现出高度的空间稳定性。由此可见，在2006－2009年期间内全国大部分省域仍尚未脱离其初期的集群范畴，区域科技创新人才队伍建设水平显示出明确的空间路径依赖的特征。

（二）空间关联局域分析

Moran散点图难以充分揭示区域科技创新人才队伍建设综合得分的局域显著性水平，因而有必要通过空间关联局域指标（local Indicators of Spatial Association，LISA）分析对其进一步予以揭示，从局域视角剖析其集聚效应的空间特性。见表7。

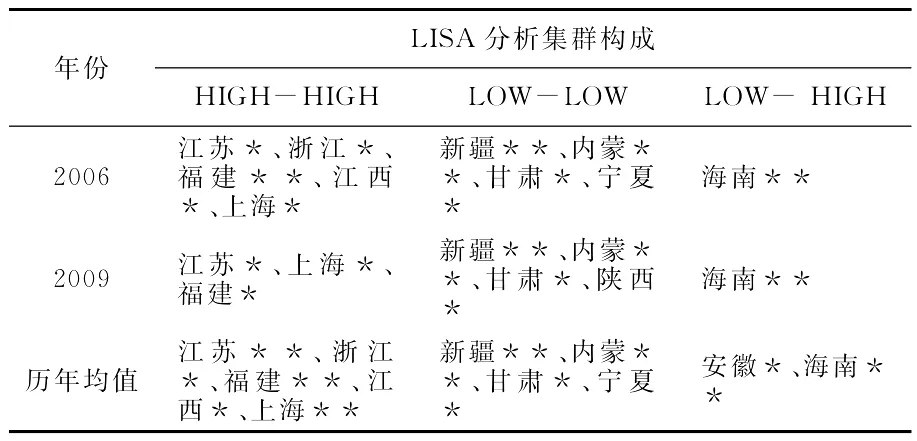
表7 区域科技创新人才队伍建设综合得分的LISA分析显著性水平和集群

表7显示了我国30个省（市）区2006－2009年期间科技创新人才队伍建设综合得分平均值的局域空间自相关LISA显著性水平和LISA集群状况，从表7中可以看出，江苏、上海、浙江、江西、甘肃和宁夏等6个省域的科技创新人队伍建设综合得分的平均值分布通过了5%的显著性水平检验，新疆、内蒙、福建和海南4个省域的科技创新人才队伍建设综合得分的平均值分布通过了1%的显著性水平检验；在表7中，HIGH－HIGH（科技创新人才队伍建设高水平－高的空间滞后）和LOW－LOW（科技创新人才队伍建设低水平－低的空间滞后）所标示的省域为集群效应发挥的中心区域，江苏、浙江、福建、江西和上海5个省域为HIGH－HIGH型集群省域；新疆、内蒙、甘肃和宁夏4个省域为LOW－LOW型集群省域；海南省属于LOW－HIGH（科技创新人才队伍建设低水平－高的空间滞后）类型。虽然Moran＇s I统计值的全局空间自相关分析表明，北京、上海、天津、福建、浙江、江苏、江西等省域位于第一象限，但发挥集群效应的中心区域仅有5个，分别为浙江、福建、江西、江苏和上海。同时，虽然黑龙江等省域位于第三象限，但发挥集群效应的中心区域亦仅有4个，分别包括新疆、内蒙、甘肃和宁夏。上述科技创新人才队伍建设水平高的集群省域和科技创新人才队伍建设水平低的集群省域在空间上的分化，显示出我国区域科技创新人才队伍建设水平综合得分已初步形成相对稳定的核心－边缘空间分布格局，表现为：局域高值以福建、江西、江苏、上海、浙江等省域作为其核心地带；局域低值以新疆、内蒙、甘肃和宁夏等省域作为其边缘地带。表7中列出了评价区间内期初（2006年）和期末（2009年）区域科技创新人才队伍建设水平综合得分的LISA显著性水平及LISA集群，从中可以清晰地看出，集群效应发挥的中心区域范围在评价期间内的变动很小，表明我国区域科技创新人才队伍建设水平综合得分的核心－边缘空间分布格局较为稳定。

三、结 论

本研究从我国省域科技创新人才队伍建设的现状评价及其空间集聚效应检测角度出发，依托于多指标综合评价体系，通过GPCA模型和ESDA方法的综合运用，在得到我国省域科技创新人才队伍建设水平综合评价得分之后，从全域视角对其空间相关性的Moran＇s I统计值予以检验，并从局域视角进行进一步分析。结果表明：

第一，2006－2009年期间，东、中、西三大地带的各省域的科技创新人才队伍建设现状综合评价得分均有不同幅度的提升，同东部地区相比，中、西部地区的提升幅度更大，区域发展差距有所降低。

第二，科技创新人才队伍建设水平较高的地区大多位于东中部沿海、沿江地区；科技创新人才队伍建设水平较低的地区则大多位于中西部内陆地区。省域间科技创新人才队伍建设水平发展的不均衡分布特征较为显著，且存在着明确的空间自相关现象和集聚效应。

第三，各地区科技创新人才队伍建设水平的时空跃迁类型呈现出较高的空间稳定性。与2006年相比，2009年除山东、湖北和贵州三个省域，其他各省域均未脱离2006年原有的集群范畴，区域科技创新人才队伍建设水平的时空演化具有较为显著的路径依赖性。

第四，省域科技创新人才队伍建设水平已初步形成较为稳定的核心－边缘空间分布格局。表现为：局域高值以福建、江西、江苏、上海、浙江为代表的东南地区和长三角地区为其核心地带，局域低值以新疆、内蒙、甘肃和宁夏等西部地区为其边缘地带。

综上所述，我国省域科技创新人才队伍建设的现阶段，需要根据各省域自身的现状水平及其特点制定相应的人才队伍建设方案。由于以甘肃、宁夏、新疆、内蒙等为代表的科技创新人才队伍建设水平低的集群省域已成为其边缘地带，且相当部分地区属于民族地区，故应考虑将上述地区作为科技创新人才队伍建设工作中的重中之重来进行规划，针对其薄弱之处拟定改进方案，制定合理的科技创新人才培养目标，充分整合政府、高校、科研机构和企业等多方力量，为科技创新人才队伍的建设搭建起良好平台。具体而言：在人才投入层面，上述省域应加大R＆D人员的投入力度，尤其是大中型工业企业和高技术产业R＆D人员的投入力度，为科技创新人才队伍建设奠定雄厚的人力资本；在人才产出层面，上述省域应提供更进一步的优惠政策，以促进大中型工业企业新产品的研发、销售并大力提升高技术产业的产值，同时鼓励发明创造，实现专利事业的长足进步，为科技创新人才队伍建设提供坚实的政策保障；在创新环境层面，应进一步加大R＆D经费的投入力度，尤其要重视大中型工业企业R＆D投入强度，同时着力打造有利于科技创新人才队伍成长的生态环境。而对于以福建、江西、江苏、上海、浙江为代表的科技创新人才队伍建设水平高的集群省域，应充分发挥出这些核心区域人才队伍建设方面的辐射带动作用，进一步完善政策制度，合理分配现有资源，规范技术市场，从而使其科技创新人才队伍建设水平在一个新的高度上获得提升。

[1] 曹文瑞．医学科技人才评价指标体系及综合评价方法研究[D]．南方医科大学，2007：7－39．

[2] 王宇婷．区域科技人才开发水平评价模型研究[D]．天津大学，2008：1－40．

[3] 高真真．区域科技人才投入产出效率评价研究[D]．天津大学，2008：1－51．

[4] 刘保民．河南省科技人才开发与评价研究[D]．天津大学，2008：1－123．

[5] 何荣旺，刘 伟，查建中等．基于灰色系统理论的科技人才资源优化配置[J]．系统工程与电子技术，2003，25（6）：678－681．

[6] 沈春光，陈万明，裴玲玲．区域科技人才创新能力评价指标体系与方法研究[J]．科学学与科学技术管理，2010：196－199．

[7] Anselin，Luc．Spatial Econometrics：Methods and Models[M]．Dordrecht：Kluwer Academic Publishers．1988：50－270．

[8] 丁 刚，胡联升．中国区域人口安全发展态势及其空间集聚效应研究——基于GPCA模型和ESDA方法[J]．哈尔滨工业大学学报：社会科学版，2010，12（6）：84－87．

[9] Rey，S．Spatial empirics for economic growth and convergence[J]．Geographical Analysis，2001，33：195－214．