中国证券市场非线性结构研究——基于混沌和GARCH模型的对比分析

邹裔忠

(武夷学院商学院，福建武夷山354300)

中国证券市场非线性结构研究
——基于混沌和GARCH模型的对比分析

邹裔忠

(武夷学院商学院，福建武夷山354300)

文章基于混沌和GARCH两类非线性结构模型对中国证券市场的实证和对比分析，验证了中国证券市场同时包含了混沌和GARCH两类非线性结构。中国证券市场存在三类投资者:正反馈投资者、逆反馈投资者和噪音交易者。正反馈投资者和逆反馈投资者具有不同投资策略与不同预期，噪音交易者受随机误差信念影响，三类投资者相互作用引起了证券价格波动的聚类性、长记忆性和持续性等非线性特征。

混沌;GARCH模型;BDS检验;非线性结构

现代金融经济学建立在理性经济人和有效市场假说的基础上，证券价格的调整反映了任何新的公开得到的信息，这是以线性、理性和秩序为特征的研究范式。但是，大量实证说明证券价格时间序列并不完全满足理想的线性假设，存在着丰富的非线性结构，常见的有:尖峰肥尾特征的非正态分布、自回归条件异方差(GARCH)模型捕捉到的波动率聚类现象、自回归分形积分移动平均(ARFIMA)模型刻画的长期记忆现象、混沌理论能够体现的时间标度上的自相似特征等。这些现象中，GARCH模型在金融时间序列分析中的应用是最广泛的，而混沌是近十年才被引入到金融来的，它们有着不同的非线性结构和不同的作用机制:GARCH模型表现为方差的非线性性，是由资产基本面无关的信息的噪音交易引起资本市场的波动，是一种外部冲击下的随机漫步;而混沌表现为均值的非线性性，是一种由确定的非线性方程产生的貌似随机的非线性动力学系统，资产价格的波动是一种内在机制产生的内随机。因此，对他们进行对比分析具有重要的理论和实际意义，而相关的研究文献比较少。M．Shintani和O．Linton(2004)用ARCH模型的模拟出数据，求出该数据最大Lyapunov指数为负数，[1]说明GARCH效应中并没有包含混沌动力性。笔者(2012)用BDS统计量检验出我国证券市场的非线性结构类型只能是混沌或非线性随机过程(如:GARCH模型)。[2]本文为了检验金融时间序列是否同时包含了混沌和GARCH两种非线性结构，对混沌和GARCH进行对比分析。

一、中国证券市场非线性结构的BDS统计检验

BDS统计量是1986年由Brock、Dechert和Scheinkman提出的假设检验的统计量，用来检测时间序列是否满足独立同分布的原假设。BDS统计量是基于相关维数估计设计出来的，能够探测常用统计检验不能检测到的非平稳性和非线性性，因而在非线性检验中具有很强的功效性。BDS检验的思想是:对于一个时间序列，假设它满足独立同分布，可由向空间重构的方法构造k维嵌入向量为=(xt，xt+k，…，xt+k－1)'，把上述嵌入向量看成k维空间中的一个点，如果确实满足独立同分布的原假设，那么嵌入向量应该在k维空间中看不出样式来。从而，相关性求和应该满足关系:

数据选取1997年1月3日至2012年2月24日的上证综合指数的日数据(记为shd)和周数据(记为shw)，1997年1月3日至2012年2月24日的深证成份指数的日数据(记为szd)和周数据(记为szw)，构建两个不同时间频率的时间序列。因为研究的是收益的时期行为，使用连续复利收益率:

用Eviews 6对上述四个证券收益率进行BDS统计检验，结果见表1。可以看出在1%显著性水平下，BDS统计检验都显著地拒绝独立同分布的原假设，说明我国证券市场具有非线性结构。日数据的z统计量都大于周数据，有更充足的理由拒绝原假设，说明日数据比周数据具有更为显著的非线性特征。

表1 证券收益率非线性结构的BDS统计检验表(ε/σ=1．5)

二、混沌和GARCH模型的对比分析

(一)GARCH模型

GARCH模型是Bollerslev在1986年提出的，是对Engle 1982年提出的ARCH模型的推广。这些模型能够捕捉金融资产收益率时间序列中广泛存在的波动率聚类(volatility cluster)现象，大量的实证研究说明了GARCH模型在金融中有广泛的适用性。波动率聚类现象指的是波动率可能在一些时间段上高，而在另一些时间段上低，不规则地混合着。模型AR(m)－GARCH(p，q)的数学形式为:

其中α0＞0，αi≥0(i=1，…，p)，βj≥0(j=1，…，q)。可知时间序列{Rt}的方差ht是时变的，是非线性结构，而其均值是线性的。

(二)混沌和GARCH融合的模型

用Mackey－Glass方程和logistic方程两个混沌模型建立非线性的均值，用GARCH模型建立非线性的方差，两者融合为一个新的非线性模型:GMG－GARCH(p，q)模型，[4]如式(3．2)。

GMG－GARCH(p，q)模型可能用准最大拟然法(quasi maximum likelihood)来进行估计。模型中有三个参数:c、τ和j，用LR检验(likelihood ratio test)来选择最优的参数组合，由于它们决定了系统的维度，对整个模型的估计是很重要的。LR统计量是分别计算在约束和无约束条件下的参数估计值，再用假设检验的方法验证二者的对数似然函数是否足够接近。假设无约束条件下模型估计的对数似然值为L1，加入m个约束项后的模型估计的对数似然值为L2，则LR统计量为:

(三)实证对比分析

对比分析的思路是:用含有混沌和GARCH两类非线性结构的GMG－GARCH(1，1)模型对收益率时间序列进行拟合，并与只含有GARCH一种非线性结构的AR(1)－GARCH(1，1)模型的拟合结果进行对比，并且对比上述两模型残差的BDS检验结果。如果模型残差的BDS检验结果表明其不存在非线性结构，则说明模型捕捉到了证券收益率时间序列中的非线性性。如果前模型比后模型捕捉到了证券收益率时间序列更多的非线性，则可以说明我国证券市场同时包含了混沌和GARCH两种非线性结构。

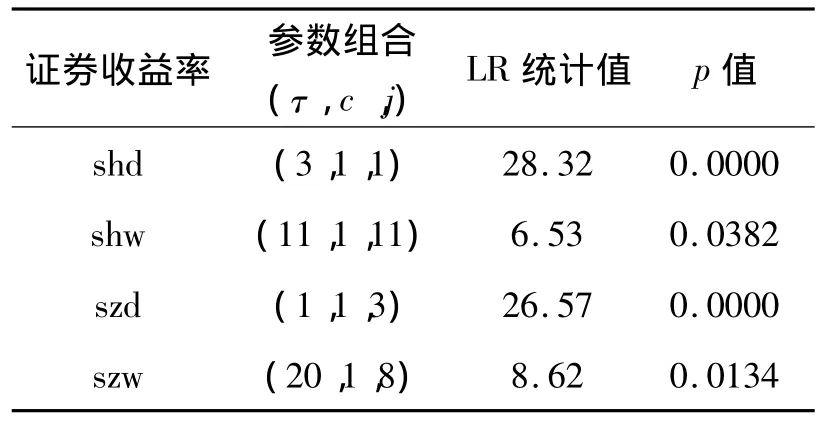
表2 GMG－GARCH(1，1)模型的拟合结果表

表3 证券收益率混沌和GARCH 拟合结果对比表

首先，把GMG－GARCH(1，1)模型对收益率时间序列进行拟合。模型中的参数c、τ和j的选择是难点，通过排列的方式把三个参数分别从1至30的所有组合方式进行拟合，通过LR检验从中选出最优的模型，作为最终的GMG－GARCH(1，1)模型，拟合结果见表2。

其次，比较GMG－GARCH(1，1)模型和AR(1)－GARCH(1，1)模型两个模型的拟合结果。见表3，可知，GMG－GARCH(1，1)模型有以下两个特点:

(1)混沌与GARCH模型融合得很好。因为GMG－GARCH(1，1)模型与AR(1)－GARCH(1，1)模型共有的异方差项β1ht－1都是高度拟合的，并且系数估计值、z－统计值和p值都很相近。

(2)GMG－GARCH(1，1)模型能更好地拟合证券收益率。对比两个模型均值中共有的δRt－1项的拟合情况，GMG－GARCH(1，1)模型的δ系数对应的z－统计值大部分变大了，p值降低了，说明对该项的拟合的更好。

最后，比较GMG－GARCH(1，1)模型和AR(1)－GARCH(1，1)模型两个模型的残差的BDS检验结果。见表4，可以看出两个模型都只能接受原假设，说明两个模型都捕捉到了证券市场中的非线性性，但是GMG－GARCH(1，1)模型的BDS统计检验对应的z统计量大多(除了个别外)比AR(1)－GARCH(1，1)模型的要小，有更充分的理由接受原假设，这就验证了GMGGARCH模型捕捉到了更多的非线性，那么捕捉到的这些更多的非线性性就是由混沌的非线性结构产生的，说明我国证券市场同时包含了混沌和GARCH两种非线性结构。

表4 证券收益率混沌和GARCH残差BDS检验对比表(ε/σ=1．5)

(四)实证结果的理论解释

上述实证结果表明我国证券市场同时包含了混沌和GARCH两种非线性结构，两种非线性结构的作用机制是不同的。非线性均值结构的两个混沌模型Mackey－Glass方程和logistic方程分别可以写为:R(当c=2和τ=1时)和(当j=1时)，两个方程都能代表非线性的交易策略，股票价格的放大影响着投资者对将来股票价格波动的预期，对Rt的影响方式前者是乘法方式，后者则是加法方式。前者代表了正反馈交易引起的动力性渗入模型中，正反馈交易者在价格上涨时买入下跌卖出;而后者是对市场中的逆反馈结构进行建模，逆反馈交易者采取的是低买高卖策略。经济意义就是混沌使证券市场价格表现为非线性性，是由具有不同投资策略和不同预期的异质投资者内在的反馈作用机制引起的。

模型中非线性方差结构的GARCH部分，可以用证券市场中的噪音交易者行为来解释，噪音交易指的是用资产基本面无关的信息(例如错误信息)所作的交易行为。所以，噪音交易者是受随机误差信念影响的交易者，体现的是由外部冲击产生的外部随机性。

证券市场上的正反馈投资者、逆反馈投资者和噪音交易者三类投资者相互作用，最终引起了证券价格波动的聚类性、长记忆性和持续性等非线性现象。

三、结论与建议

在方差为非线性结构的GARCH模型的基础上，加入Mackey－Glass方程和logistic方程两个混沌模型建立非线性的均值，得到一个新的含有混沌和GARCH两类非线性结构的GMGGARCH模型，并与GARCH模型进行对比分析，实证结果表明我国证券市场同时包含了混沌和GARCH两种非线性结构。

因为两种非线性结构的作用机制不同，为了使我国证券市场更加成熟，应该同时从两方面进行改革:一方面要加强虚假信息和内幕信息的监管力度，建立有效的信息传播体制，这样可以降低噪音交易对证券市场价格的影响;另一方面要加强投资者的教育，培育投资者价值投资的理念，这样可以减少由于正反馈投资者和逆反馈投资者过度投机，使证券市场更加平稳和成熟。

[1] Mototsugu Shintani，Oliver Linton．Nonparametric neural network estimation of Lyapunov exponents and a direct test for chaos．Journal of Econometrics，2004(5)．

[2] 邹裔忠．中国证券市场非线性结构的实证检验[J]．铜陵学院学报，2012，(1)．

[3] [美]Ruey S．Tsay．金融时间序列分析[M]．潘家柱译．北京:机械工业出版社，2006．

[4] Kyrtsou，C．Heterogeneous non-linear agents’strategies and routes to chaotic dynamics．Working Paper，LAMETA，University of Montpellier I，2006．

[5] Mackeym C，Glass L．Oscillation and Chaos in Physiological Control System．Science，1977(7)．

[6] Farmer J D．Chaotic Attractors of Infinite-Dimensional Dynamical Systems．Physica D，1982，4．

F830

A

1672-0040(2012)04-0016-05

2012-03-28

邹裔忠(1979—)，男，福建泰宁人，武夷学院商学院讲师，经济学硕士，主要从事金融计量和物流金融研究。

(责任编辑 郑东)