ARCH模型族在深圳成指中的应用

丁扬恺

(浙江师范大学数理信息学院，浙江 金华，321004)

随着金融市场的急剧发展，大量的理论和实证研究发现了金融资产的收益率和波动率的一些特征，这些金融资产的波动率在期权定价以及金融风险管理等领域有着重要的作用。然而，我们在研究金融市场时却发现，大多数时间序列的误差项序列线性无关，这就使得经典的最小二乘法失效。1982年Engle提出了自回归条件异方差模型[1−2]，1986年Bollerslev提出了广义 ARCH模型[3]，他们均很好地模拟了这种波动性。考虑到金融资产中收益率与风险成正比，即风险越大，收益率就越高，人们在GARCH模型的基础上，引进了GARCH-M模型[4]。为了贴近现实，人们还提出了EGARCH模型[5]，因为金融资产的价格下跌比相同幅度的价格上涨对资产价格波动的冲击更大，人们通常认为负的冲击比正的冲击对收益率的波动影响更大[6−7]。此外，CARCH模型[8]可以很好地模拟条件方差的均值。如今ARCH模型族已成为衡量金融市场波动性的强有力工具。

一 、金融时间序列模型概述

1.ARCH模型

ARCH模型的主要思想是：扰动项μt的条件方差依赖于它的前期值μt−1的大小。假设预测误差 yt为实随机变量，随机误差项的条件方差与其误差项滞后的平方有关，则一个ARCH(p)过程如下：

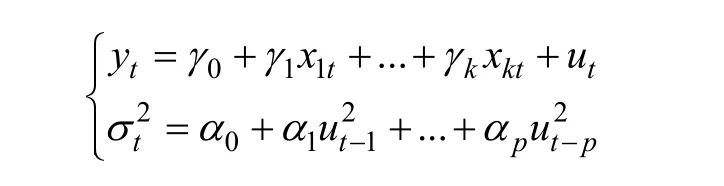
若检验模型估计结果所得的残差序列的条件方差存在上面的形式，则表明其具有ARCH效应。

2.GARCH模型

GARCH模型在误差项的条件方差中加上了误差项条件方差的滞后项，从而可以体现更为灵活的滞后结构。GARCH(p,q)的方差方程定义为：

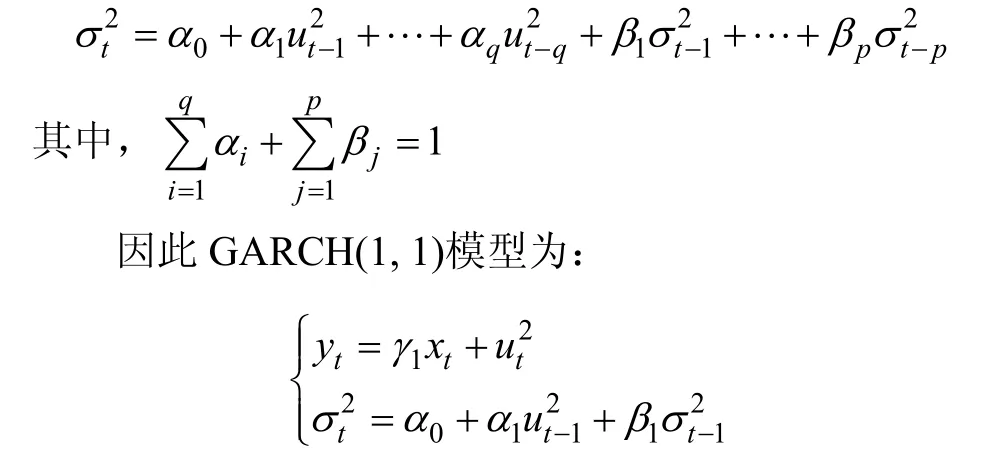
GARCH 模型的优点在于它考虑到了金融事件序列的波动集群性，并且可以有效地排除资产收益率中的过度峰值(Excess kurtosis)。为了准确表示金融中高风险高回报，将金融资产收益率的条件方差引入到GARCH模型的均值方程中，得到GARCH-M模型：

条件方差 σt代表了期望风险的大小。所以GARCH-M模型适合描述一些期望回报与期望风险密切相关的金融资产。

3.EGARCH模型

EGARCH模型被称为指数GARCH模型。为了简单说明，考虑EGARCH(1,1)模型，其将条件方差设定为如下形式：

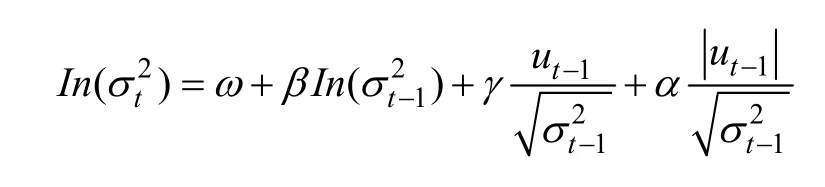
上式即使参数估计是负数，条件方差2ts仍然是正数。如果参数γ<0，则表明存在杠杆效应；如果参数γ=0，则表明不存在非对称效应。

二、实证分析

本文选取深证成指(399001)日收盘价作为研究对象，数据截取时间自1991年11月4日到2011年5月16日，总共4760个数据，数据来源于中信金通证券有限责任公司。

为了减少估计时的舍入误差，我们取深证成指日收盘价的自然对数序列，建立随机游走模型，用Eviews6.0得如下模型估计结果：

即：

其中R2=0.998805。图1给出了深证成指日收盘价的自然对数收益率时序。

从图1中可以看到，回归方程的残差表现出波动“聚集性”，即大的波动后面常常伴随着较大的波动，较小的波动后面的波动也较小，残差序列的这种特性表明其可能存在条件异方差性，即ARCH效应。接下来我们采用 ARCH-LM 检验该随机游走模型残差的ARCH效应。

图2中F统计量=41.10343，其概率值P非常小，表明检验辅助回归方程中的所有滞后残差平方项是联合显著的；ARCH效应的检验统计量是 Obs*R-squared，其值等于 703.2013，相应的概率值P非常小，即可认为残差序列存在条件异方差。下面用GARCH-M模型、EARCH模型分别来刻画这种特性。

图1 深证成指日收盘价的自然对数收益率时序

图2 深证成指日收盘价(ARCH-LM检验)

首先根据收益率 r的分布直方图3，深圳成指收益率序列具有尖峰(Kurtosis=9.32443>3)，非对称性(Skewness=0.197>0)，以及零均值(对均值为零做假设检验)等特征，这些特征对一般金融资产收益率也是普遍存在的。由于深圳成指收益率表现出“尖峰厚尾”，即比正态分布具有更厚的“尾巴”，所以对μt用 GED分布(广义误差分布)能够比正态分布假设更好地描述收益率序列的这种厚尾特征。假设投资者应该为承担额外的风险而获得更高的收益，我们将深圳成指收益率的条件方差引入到GARCH模型的均值方程中，得到GARCH-M(1，1)的估计结果，见表(1)。

估计出的方程的所有系数都很显著，并且ARCH及GARCH项之和接近于1，即收益的波动冲击影响会持续很长一段时间才会逐渐衰减；其次均值方程中的σt的系数δ为0.112480，表明市场中的预期风险增加一个单位，就会导致收益率也相应地增加0.112480个百分点。同时还可以画出GARCH-M模型的条件方差(见图4)。从图4中看到从700～1400时间段(即1994年7月28日至1997年6月23日)条件方差较大，从而表明深圳成指在这段时间内存在较大波动；从1401～4000(即1997年6月21日至2008年3月28日)条件方差波动较小。

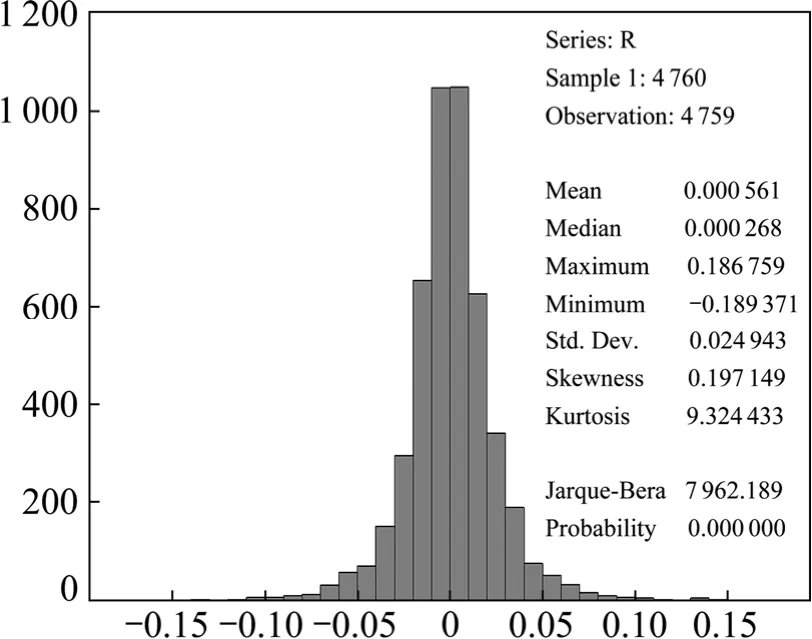
图3 深证成指日收盘价分布直方图

尽管GARCH-M模型能够很好地解释深圳成指收益率序列的波动“聚集性”，但它不能解释深圳成指收益率序列存在的“杠杆效应”，即利空消息(收益率的下跌)是否比同样程度的利好消息(收益率的上涨)产生更大的波动。因此需利用ARCH模型族中的EGARCH模型来合理检验深圳成指收益率的“杠杆效应”，见表2。

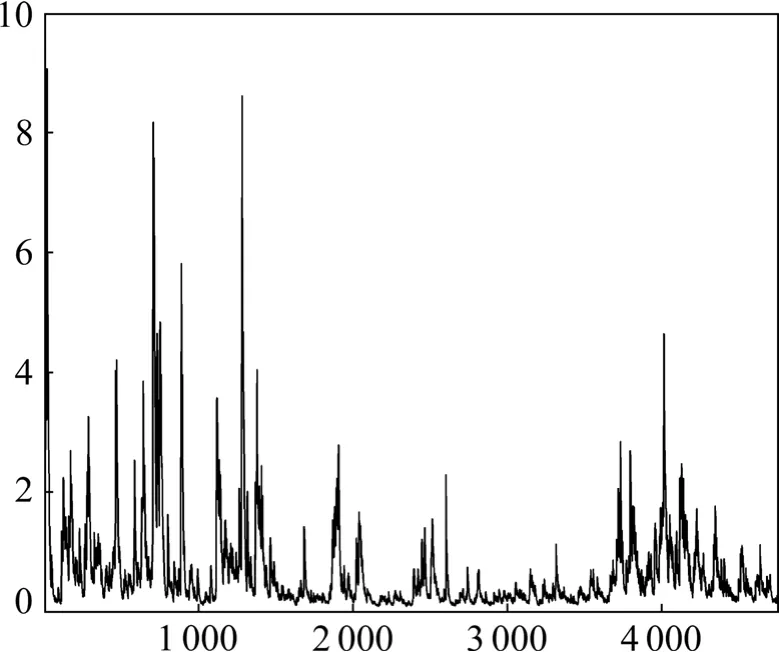
图4 深证成指日收盘价的条件方差

由表(2)可以看出，α的估计值为0.270791，非对称项 γ的估计值为−0.018678，两者的统计量都很显著。当μt−1>0(利好消息)时，该信息冲击对条件方差的对数有一个0.270791+(−0.018678)=0.2521倍的冲击；而当μt−1<0(利空消息)时，它给条件方差的对数带来的冲击为0.270791+(−0.018678)*(−1)= 0.2895倍。

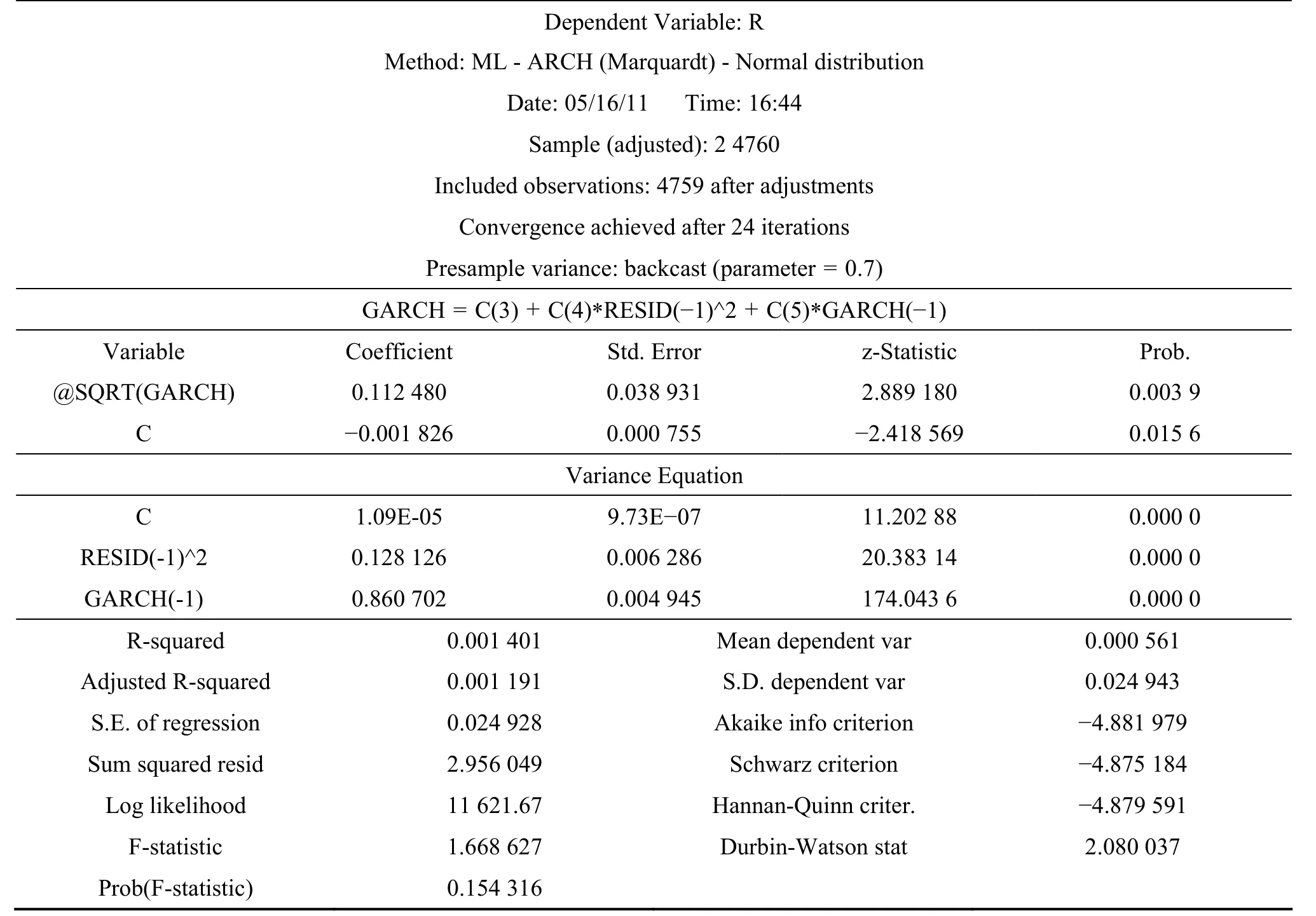
表1

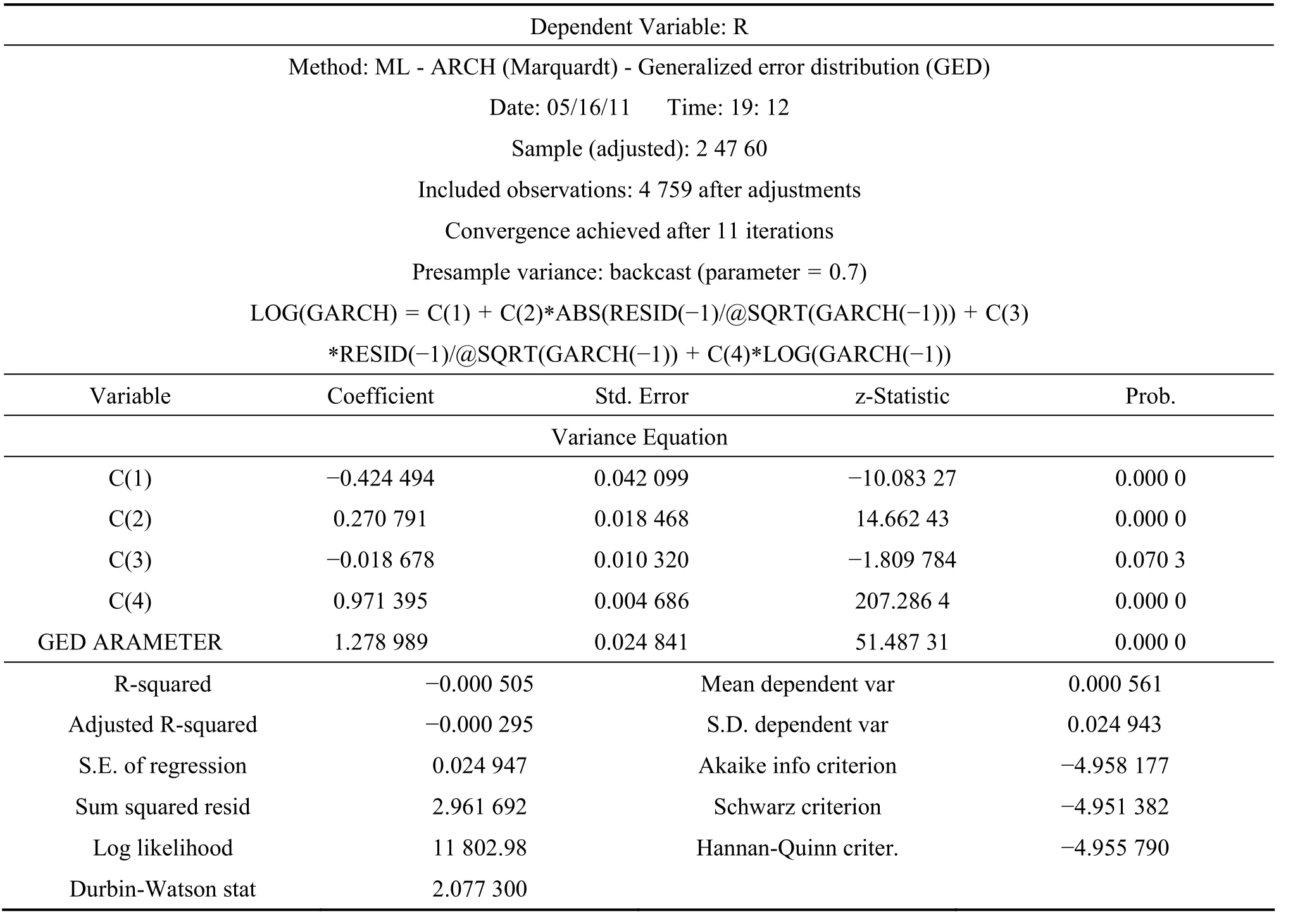
表2

为了清晰地表明利好消息与利空消息冲击的影响，我们根据 EGARCH模型的结果，绘制出相应的信息影响曲线，见图5。从图5中可以看到，这条曲线在信息冲击小于 0时(代表利空消息)比信息冲击大于 0(代表利好消息)稍微陡峭点。这就说明了利空消息的冲击使得波动性的变化更加大一些。

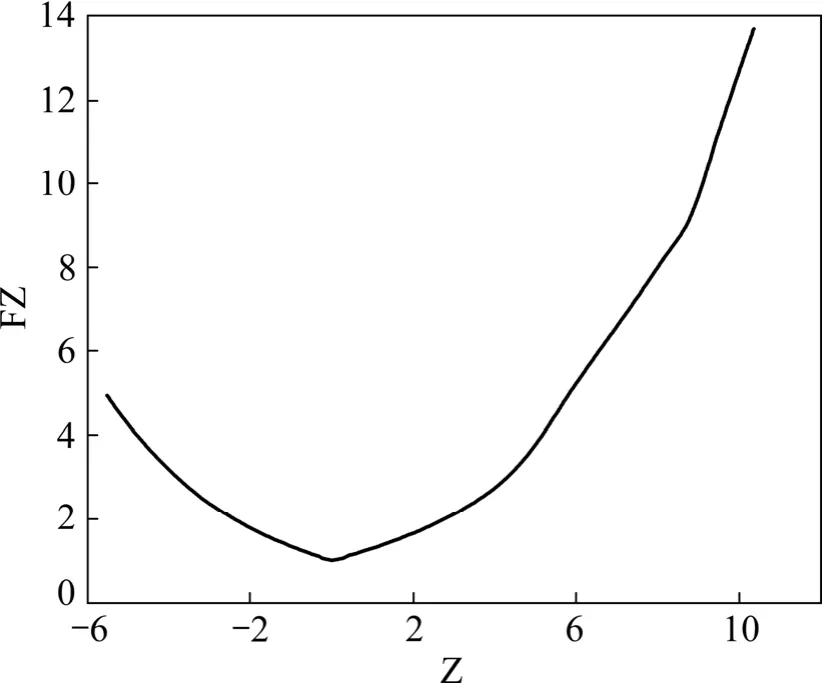
图5 深证成指日收盘价的信息冲击曲线

三、结语

以深圳成指1991年11月4日至2011年5月16日收盘价为样本，对ARCH效应、波动聚集性、杠杆效应分别进行合理的模型分析中可以得出以下结论。

首先，深圳成指价格波动非常大，呈现非正态分布，具有非对称性及波动集簇性；其次深圳成指具有明显的ARCH效应，用GARCH-M模型估计可知当市场中的预期风险增加一个单位，就会导致收益率也相应地增加 0.112480个百分点，收益的波动冲击影响会持续很长一段时间之后才会逐渐衰减。再次，通过 EGARCH模型分析可知利空消息的冲击使得波动性的变化更加大一些，这也为之后更好地运用VAR等工具进行期货市场的风险管理奠定了较好的基础。最后我们发现，GARCH-M 模型的对数似然值为11621.67，AIC为−4.8819，SC为−4.8751；而EGARCH模型的对数似然值为11802.98，AIC为−4.9581，SC为−4.9513。故实际中投资者应选取EGARCH模型对深圳成指的预测较为理想。

[1]Engle,Robert.Autoregressive conditional heteroskedasticity with estimates of the variance of U.K [J].Econometrica,1982(50): 987−1008.

[2]Engle,RUSSELL J.Autoregressive conditional duration: a new model for irregular spaced transaction data [J].Econometrica,1998(66):1127−1162.

[3]Bollerslev,Tim.Generalized autoregressive conditional heteroskedasticity [J].Journal of Economics,1986(31):307−327.

[4]万蔚.我国沪,深股市的波动性研究—基于 GARCH族模型[J].价值工程,2007(10):14−18.

[5]邓尧天,杜子平.EGARCH 模型在同业拆借利率预测中的应用[J].湖北民族学院学报,2007,25(2):234−237.

[6]杨妍妍,岳宏远.我国中小企业板非对称性的实证研究[J].时代金融,2008(4): 51−53.

[7]吴毅芳,彭丹.我国股票市场价格波动的非对称性及其国际比较[J].中南大学学报(社会科学版),2007,13(5): 568−572.

[8]EVDOKIA X,STAVROS D.ARCH Models for Financial Applications [M].Athens University of Economics and Business,Greece,2010:19−55.