前缘引流对船舶阻力及伴流分布的影响

2012-01-22,,

船海工程 2012年5期

(武汉理工大学交通学院，武汉 430063)

对于中低速船，特别是肥大船型，粘性阻力占总阻力的80%～90%[1]，其中的形状阻力部分也占有较大比重。国内外实验研究[2]已经证明,钝体前缘开孔引流对周围流场特别是艉流场有改善作用，钝体形状阻力明显减小。本文针对形状阻力占较大比重的船型，采用数值模拟方法，设计前缘开孔，在船艏高压区设引流入口，船艉设出流口，引流通道贯穿全船。分析在不同开孔形状、开孔尺寸和出流位置下的船舶艉部流场特性和阻力变化规律，为减阻船型优化设计提供参考。

1 数值方法

1.1 控制方程(张量形式)

船体绕流数值计算中，认为流体均质不可压，在直角坐标系下，由质量守恒得到的连续性方程为

(1)

由动量守恒得到的Navier-Stokes方程为

i,j=1,2,3

(2)

式中：ui,uj——速度矢量u在xi、xj方向上的分量；

ρ——流体密度；

p——压力；

υ——运动粘性系数；

Fi——体积力,此处为重力gi[3]。

1.2 k-ω湍流模型

k-ω模型通过引入湍动能和比耗散率的输运方程得到k和ω，把μt表达为k和ω的函数。其输运方程为

(3)

式中：Gk——由于时均速度梯度引起的湍动能；

Gω——ω的产生项；

Γk,Γω——k和ω的有效扩散系数；

Yk,Yω——由湍流引起的k和ω的耗散项;

Sk,Sω——自定义源项[4]。

1.3 边界条件

对本文定常不可压缩粘性绕流场的叠模计算，主要用到4种边界条件。

1)速度入口:u=u∞,v=w=0；

3)壁面边界满足无滑移条件:u=v=w=0；

式中：u,v,w——速度矢量υw沿X、Y、Z方向的分量。

1.4 数值求解

采用基于单元中心的有限体积法数值求解控制方程。速度和压力耦合采用SIMPLEC算法；压力离散采用Standard格式；动量和湍动能离散采用二阶迎风格式；比耗散率离散采用一阶迎风格式。

2 物理模型及计算域

选择一条双艉无球艏的中速船为研究对象，采用1∶8.3的比例建模。模型主尺度见表1；横剖线视图和模型底部三维视图分别见图1和图2；计算域及尺寸划分见图3，图中Core区域为船体。计算中假设船舶正浮，无偏航，不考虑自由面影响，仅研究船舶粘性阻力。

表1 模型主要尺度

图1 横剖线图

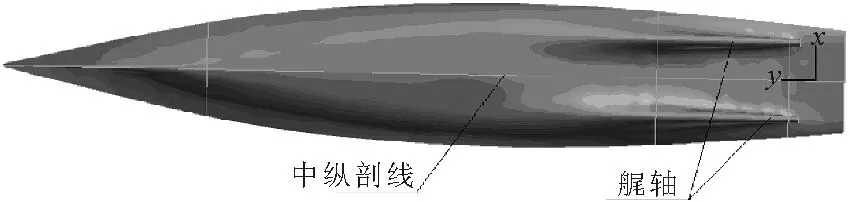
图2 底部三维视图

图3 计算域

计算模型共选择3种开孔形状：方孔、圆孔(侧面)、圆孔(中间)；3种出流口位置分别为：艉封板、1#～2#站、3#～4#站。

4种入流面积分别为：3.6%、1.8%、1.0%、0.5%(入流口面积与船模最大横截面积百分比)。为直观表达引流通道的参数信息，3种通道类型的艉部视图见图4。

为方便分析比较，将开孔引流模型按顺序编号MODE1～21。所有开孔引流模型的参数方案见表2。

表2 开孔引流模型参数方案

表2中，圆孔(中间)表示模型引流通道关于中纵剖面对称；圆孔(侧面)表示模型引流通道完全位于中纵剖面一侧；“%”表示引流入口或者出口的面积占模型最大横剖面面积的百分比，用来表征通道尺寸大小。

3 数值计算结果及分析

3.1 计算结果

方孔、圆孔(侧面)、圆孔(中间)引流模型阻力计算结果以及与原型比较的减阻率见表3。

表3 方孔引流模型阻力计算结果

注：Cvp-粘压阻力系数；Cf-摩擦阻力系数；Cv-粘性阻力系数[1]；ΔCvp-粘压阻力系数减阻率，定义为ΔCvp=(Cvp-Cvp*)/Cvp*；ΔCf-摩擦阻力系数减阻率，定义为ΔCf=(Cf-Cvf*)/Cf*；ΔCv-粘性阻力系数减阻率，定义为ΔCv=(Cv-Cv*)/Cv*；Cvp*、Cf*、Cv*分别为对应的原型船模阻力系数。

3.2 计算结果分析

3.2.1 开孔形状对总阻力的影响

图5显示不同开孔形状下的模型粘性阻力系数变化情况。横坐标上a，b，c分别代表方孔、圆孔(侧面)、圆孔(中间)引流阻力系数。结果显示：引流后粘性阻力系数增加值：a>b>c，即方孔引流粘性阻力系数增加最大，圆孔(中间)引流阻力系数增最小。这是因为方孔引流通道内存在拐角，易产生漩涡，增加了对流动的干扰，导致阻力增加较多，圆孔引流通道内壁光顺，避免了漩涡的生成；相同入口面积条件下，圆孔(侧面)引流通道的湿面积较圆孔(中间)引流通道湿面积大，导致总的摩擦阻力系数较大，故总的粘性阻力系数较圆孔(中间)也偏大。

图5 不同开孔形状模型减阻率比较

3.2.2 出流口位置对总阻力的影响

图6显示不同出流口位置的模型粘性阻力系数变化情况。横坐标上a，b，c分别代表出流口位于艉封板、1#～2#站、3#～4#站的引流阻力系数。结果显示：引流后粘性阻力系数增加值：a>c>b，即出流口位于艉封板处粘性阻力系数增加最大，出流口位于1#～2#站时阻力系数增加最小。这是因为引流至艉封板处引流通道出现艉高艏低的“爬坡”现象，不利于来流的顺利通过，导致管道内阻增加较多；相反，引流至3#～4#站时通道出现艏高艉低现象，引流通道倾斜角度很大，明显改变了来流方向，导致内阻增大；引流至1#～2#站时，通道艏艉过渡平缓，来流能够顺利通过，因而阻力增加较小。