基于价格粘性的货币政策、股票价格与宏观经济之间动态关系研究
2012-01-15王国松
王国松
(上海大学 经济学院,上海 200444)
一、引 言
历史事件表明,股票价格由快速膨胀到急剧崩溃,往往都会引发一轮较长时间的经济衰退和通货紧缩,由此引发了各国理论界和货币决策者对“货币政策是否应该对股票价格作出反应”这一问题的高度关注与深度思考。如果股票价格包含通货膨胀信息及股市是经济的“晴雨表”的命题成立,则意味着货币政策应该对股价波动作出适度反应,以此提高货币政策的前瞻性和有效性。
关于股票价格与通货膨胀之间关系的研究,国内外学者的相关研究更多集中于“通货膨胀对股票收益的影响”这一问题,这与著名的“费雪效应”是密不可分的。费雪(1930)[1]提出,名义利率近似等于实际利率与预期通货膨胀率之和,实际利率是独立于货币因素或通货膨胀之外且由实际经济因素所决定,通货膨胀则完全由债券或股票的名义收益所体现,即通货膨胀与债券或股票的收益之间存在正向变动关系。因此,从长期来看,股票是一个好的抗御通货膨胀风险的套期保值品。国内外学者期望通过深入研究通货膨胀对股票价格和股票收益的影响,回答“通货膨胀能否预测股市波动”以及“股票是否是有效的抗御通货膨胀风险的套期保值品”等长期争议的焦点问题。[2-4]总体而言,关于股票价格对通货膨胀的影响以及股票价格波动是否包含通货膨胀信息等方面的研究,目前研究成果尚少。吕江林(2005)[5]实证考察了若干国家的股票价格指数与实际国内生产总值、消费物价指数之间的关系,发现股票价格指数与实体经济之间存在协整关系和因果关系,认为货币政策应该对股价变动作出适时反应。孙华妤和马跃(2003)、[6]郭田勇(2006)、[7]武戈(2007)[8]等人认为,资产价格变动将通过投资效应、资产负债表效应、流动性效应、财富效应、托宾Q效应等多种渠道作用于总需求和通货膨胀,货币政策应该关注资产价格变动。王虎、王宇伟和范从来(2008)、[9]王国松(2010)[10]等人的实证研究表明,我国股票价格的变动能够引起未来CPI和WPI的同向变动,与CPI的关系非常稳定;股票价格在一定程度上包含了我国未来通货膨胀的信息。
那么,股市到底是不是经济的“晴雨表”以及股价为何背离宏观经济面而运行?诸多研究成果否定了股市是经济的“晴雨表”,并解释了股票价格背离基本面的成因。伍志文、鞠方(2003)[11]7指出,自 20 世纪 80 年代以来,通货紧缩与资产膨胀并存情形在西方发达国家经济运行中具有相当的典型性;进入20世纪90年代以来,物价下跌与资产价格膨胀在中国也客观存在。为解释通货紧缩与资产价格膨胀并存这一金融现象,伍志文、鞠方(2003)通过引入以资本市场为代表的虚拟经济部分,将传统货币数量论拓展为三部门的广义货币数量论,从货币政策角度分析了通货紧缩与资产膨胀并存的生成机理,认为“中国悖论”(即中国通货紧缩与资产膨胀并存的现象)是理论货币供给量偏松情况下货币结构严重失衡的产物,是货币结构失衡(程度)大于总量失衡(程度)的结果。[11]9-16但是这种理论解释很难说明在理论货币供给量偏松、货币结构失衡程度大于总量失衡程度的时候,为什么经济运行中总是先出现“通货紧缩与资产膨胀并存”现象,而不是“通货膨胀与资产缩水并存”现象?不仅如此,在现实经济中,同样也会出现经济持续高速增长、物价不断攀升和资产尤其是股票价格、股票价格指数不断下滑并存的现象。由此可见,这种“通货紧缩与资产膨胀并存”以及“通货膨胀与资产缩水并存”的经济现象不只是货币结构失衡的问题,需要从新的研究视角揭示其形成机理。本文拟从价格粘性的货币数量模型、货币政策传导机制以及投资者的预期自我实现理论等研究视角,分析股票价格先于通货膨胀而动的形成机理。
二、股票价格先于宏观经济而动的形成机理分析
(一)基于价格粘性的货币数量模型的分析
首先,货币不仅是商品与劳务的交易媒介,同时也是金融资产的交易媒介,为此,需要将金融资产交易引入传统的货币数量模型中,否则会夸大货币数量对商品价格与劳务价格的影响。
其次,传统的货币数量模型并没有考虑到价格粘性的存在。新凯恩斯学派认为,由于菜单成本、厂商交错调整价格和投入产出关联因素的存在,对于来自外部的冲击,商品价格呈现出了十分缓慢的调整,这种价格调整明显滞后于外部冲击的特性即为价格粘性。在价格粘性存在的情况下,当期的货币数量变动并没有在当期的商品价格中得以表现,即商品价格和金融资产价格对当期的货币供给量变动的冲击存在一个反应时滞。与商品价格相比,由于投资者对货币政策的预期作用,使得金融资产价格相对比较敏感,可以视为金融资产价格不存在价格粘性。在这种情况下,若当期的实际国民收入和金融资产数量不变,则意味着当期货币数量的变动将会通过金融资产价格的变动得以表现。伴随着商品价格粘性的逐渐消失,一次性货币供给的冲击会被金融资产价格和商品价格共同吸收,这也意味着金融资产价格对一次性货币数量变动的反应同样存在一个短期超调状态。随着金融资产价格短期超调的逐渐消失,市场将重新达到一个新的均衡状态。由此可见,在价格粘性存在的情况下,一次性货币数量的变动所引致的金融资产价格和商品价格的调整应是一个动态的均衡调整过程,金融资产价格存在一个由短期超调到重新回归均衡状态的动态调整过程。
由于经济周期的现实存在,“逆风向”操作的货币政策规则使得货币政策的扩张性或紧缩性具有明显的周期性与持续性。持续扩张性或紧缩性的货币政策必将对金融资产价格和商品价格产生持续性的同向冲击。在价格粘性存在情况下,这种持续性的同向冲击,使得金融资产价格与商品价格很难出现一次性货币供给变动冲击后的短期均衡调整过程,金融资产价格和商品价格对这种连续性扩张(或紧缩)的货币政策冲击反应,更应存在一个超调失衡的累积叠加效应,从而加剧金融资产价格的超调失衡程度及其存续时间。因此,在一个宏观经济上行或下行运行期间,由于货币政策的持续性同向操作,从而使得一般物价水平与金融资产价格在短期内难以出现一次性货币数量冲击后短期的动态均衡状态,而是存在一个较长时间的累积叠加超调或失调状态,由此导致一般物价水平的峰值与谷值的出现时间与金融资产价格的峰值与谷值的出现时间存在一个明显的滞后期,即金融资产价格将会先于一般物价到达周期性的顶部或底部。正是由于货币数量的同向连续性冲击使得金融资产价格能够在较长时间处于价格超调状态,从而使得金融资产价格的波动幅度背离其经济基本面变动幅度而产生所谓的“剪刀差”。因此,金融资产价格在其周期性运行中总是先于实体经济、通货膨胀达到周期性的顶部或底部,而不是滞后于实体经济和通货膨胀。这种现象只是表明资产价格与实体经济、通货膨胀的运行趋势在中长期存在时间上的不一致性,这种不一致性并不能够否认资产价格具有宏观经济运行“晴雨表”功能,恰恰说明金融资产价格与实体经济、通货膨胀背离而先行的现象具有较好的“信号”作用,不失为宏观经济运行的“晴雨表”。
(二)基于价格粘性的货币政策传导机理分析
基于价格粘性的货币数量分析,从表象上看,金融资产价格先于商品价格而动是一种货币现象,但也似乎很难让人信服金融资产价格是对实体经济波动作出的反应。如果从货币政策的传导机制视角来分析,可以看出,金融资产价格的波动在一定程度上体现了未来实体经济和物价的波动趋势。一次性货币供给的增加,由于商品价格粘性的存在,货币需求并没有随之增加,由此使得市场利率水平下降幅度超过其短期均衡水平,即利率处于短期超调失衡状态,由此刺激消费需求和投资需求。同时,由前文的包含价格粘性的货币数量方程和戈登方程(Gorden E-quation,1962)[12]可知,市场利率水平下降将会使得金融资产价格出现超调式上涨,再通过托宾Q效应、财富效应、资产负债表效应等传导渠道作用于消费需求和投资需求。伴随着消费需求和投资需求的增加,货币需求随之增加,物价粘性逐渐消失,物价上涨、市场利率与金融资产价格的超调失衡将得以纠正而出现市场上涨与金融资产价格下跌,市场重新达到新的均衡。其具体机理如图1所示:
从图1的货币政策传导机理可知,金融资产价格先于实体经济而动,而实体经济则先于商品价格而动,由此在现实经济活动中出现物价水平逆周期波动、资产价格膨胀与通货紧缩并存的现象。同时,货币政策的传导机理同样可以解释金融资产价格波动幅度大于实体经济波动幅度的“剪刀差”现象。由于价格粘性存在和货币政策的周期性、持续性的同向操作,使得金融资产价格在较长期间处于一个累积叠加的超调失衡状态,由此加剧了金融资产价格波动幅度与实体经济波动幅度之间的背离而出现较大的“剪刀差”。
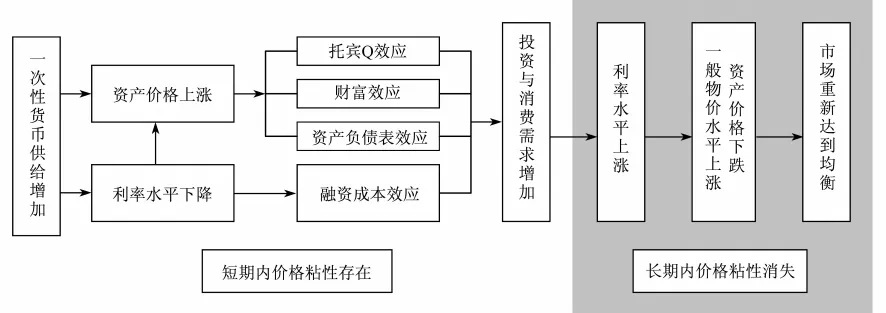
图1 价格粘性下一次性货币供给冲击后价格由短期超调至长期均衡的调整机理
此外,金融资产价格反映了投资者对未来经济的预期;而投资者的预期存在一个自我实现过程,即投资者的预期在没有外界强烈负面因素干扰下,存在一个不断自我加强的过程。故而在经济运行良好时,投资者的乐观预期更加乐观,而在经济运行不景气时,悲观预期更加悲观,从而导致市场投资者在经济趋势繁荣时期则会对“好消息”反应过度而对“坏消息反应”不足,而在经济趋于衰退时期则会对“坏消息”反应过度而对“好消息”反应不足,投资者的预期自我实现将会进一步扩大资产价格背离其基本面的“剪刀差”。因此,可以说,20世纪80年代以来资产价格变动与实体经济增长之间所呈现的“剪刀差”趋势的直接原因,是连续性宽松的货币政策与金融市场投资者乐观的自我实现因素共同作用的结果。
三、基于我国数据的实证检验
(一)数据处理与计量模型的确立
为了减少各变量序列的波动性,同时也为了较为准确反映各变量之间波动的经济关系,本文选择了各变量波动的相对值即月度同比的百分值。本文选择了1999年1月至2010年12月期间中国的月度数据作为分析对象,数据来自于中国社会科学院金融研究所(http://ifb.cass.cn/jrtj/index.asp)、中国国家统计局(http://www.stats.gov.cn/)和中国证券监督管理委员会(http://www.csrc.gov.cn/)等网站的电子数据库。文中物价指数以消费物价指数的月度同比的百分值表示(CPI);股票价格以上证综合指数的月末收盘指数同比的百分值表示(SHGZ);国内生产总值,由于缺乏GDP的月度统计数值,本文选择了以实际工业增加值月度同比的百分值表示(RGYZZ);m1和m2分别表示狭义货币供给和广义货币供给的月度同比的百分值。
在价格粘性下,货币数量变动所引致的利率超调以及资本市场上投资者预期的自我实现等冲击因素,并不是直接作用于物价水平,而是通过金融资产价格、投资需求与消费需求即国民收入的变动作用于物价水平,由此使得物价波动滞后于经济增长,经济增长波动又滞后于金融资产价格。因此,在价格粘性条件下,当期物价应为前期的物价、货币政策、金融资产价格和名义国民收入的反应函数;一方面货币供给的变动首先分别作用于资产价格和利率,再通过利率与资本市场作用于国民收入,最后作用于物价水平,即M→股价与利率→国民收入→物价;另一方面,由于通货膨胀具有一定的惯性,前期物价水平对当期物价水平具有较强正向影响。基于此,可以反向推定我国消费物价指数对实际国民收入冲击的反应滞后期为2,而对股票价格冲击的反应滞后期为3,对货币供给冲击的滞后期为3,故而可得如下计量检验模型:

(二)协整检验
为了防止回归检验中可能出现的“伪回归”现象,本文运用 Eviews6.0软件的 ADF单位根检验模型分别对CPI、RGYZZ和GZI等变量序列进行了单位根检验。检验结果如表1所示,各变量序列的ADF统计量在各临界水平均不显著,即各变量水平序列均存在单位根,是非平稳时间序列。各变量序列一阶差分的ADF统计量在1%临界水平均显著,各变量时间序列都是一阶单整序列,即I(1)。

表1 单位根检验结果
由于各变量序列均为一阶单整序列,符合协整检验的统计学要求,可以进行协整检验。本文选择了Engle和Granger(1981)提出的基于回归模型残差的协整检验法,即先进行回归方程估计,再对回归方程的残差序列进行单位根检验;如果残差序列是平稳序列,则表明回归方程的因变量与自变量之间存在协整关系,否则不存在协整关系。根据前文所设计量模型(1),本文采用OLS法对进行回归方程的估计与方程残差的ADF单位根检验,检验结果分别如方程(2)和(3)所示:

方程下方括号中的数值分别为方程对应项的标准差和t统计值的检验值,下文相同。
方程(2)残差序列的ADF单位根检验:T统计值=-13.2528***(1%水平的临界值=-2.5816,无截距、无趋势)

方程(3)残差序列的ADF单位根检验:T统计值=-13.1026***(1%水平的临界值=-2.5816,无截距、无趋势)
由方程(2)和(3)的相关系数R2、F统计量、DW统计量可知,模型估计效果比较理想。方程(2)和(3)的残差序列的单位根检验T统计值在1%临界水平显著,为平稳序列,不存在单位根。由此说明,CPIt与 CPIt-1、RGYZZt-2、SHGZt-3、mt-3之间存在着长期稳定的协整关系。从长期来看,我国当期物价水平主要取决于前期物价水平,表明我国物价水平具有较强的惯性;方程(2)和(3)同时表明,我国物价水平与股票价格之间从长期来看存在显著的正向相关,但弹性系数相对偏小,不及发达市场国家的影响力度。②吕江林(2005)对美国的实证研究发现,从长期来看,美国股指波动对其物价影响的弹性系数达到-0.2392,两者是负向相关,详见吕江林的《我国的货币政策是否应对股价波动做出反应?》,该文刊于《经济研究》2005年第2期。
(三)基于SVAR的方差分解
由于向量自回归(VAR)模型并没有直接给出变量间的当期影响关系,而是将变量间的当期关系隐含在随机扰动项之中。结构向量自回归(SVAR)模型则弥补了VAR模型这一缺点,不仅可以体现变量的同期相关关系,而且可以给出更加符合经济理论的约束设定,避免VAR方法中Cholesky分解引发内生变量排序对结果的影响。正因如此,本文选用SVAR模型实证检验通货膨胀、实际经济增长、货币供给、股票价格之间的结构性影响关系。
1.VAR模型的滞后阶数确定与平稳性检验
本文以m1、m2代表货币政策,构建两个4变量的VAR模型;其中 VAR1是以 CPI、RGYZZ、m1、SHGZ 为检验对象,VAR2是以CPI、RGYZZ、m2、SHGZ 为检验对象。依据LR、AIC、SC和 HQ信息量取值准则和经Eviews 6.0软件所输出的检验值,确定VAR1和VAR2的最优滞后阶数为4阶,即为VAR1(4)与VAR2(4)。经Eviews 6.0软件对上述两个VAR模型的平稳性检验,发现被估计VAR1、VAR2的AR特征多项式所有特征根秩的倒数均小于1,位于单位圆内,满足VAR模型的平稳性要求。
2.SVAR的识别与估计
对于本文的4元4阶VAR模型,其简化式无穷阶的向量移动平均VMA(∞)形式和结构式可以分别表示为:yt=A(L)εt和C0yt;其中,yt=(cpit,rgyzz,mt,shgzt)t=1,2,…,T,A(L)是滞后算子 L 的4×4的参数矩阵;εt是VAR模型的扰动项,为k纬的新息向量;C0为对角线元素全为1的4阶方阵,反映同期的结构关系;ut为4纬的不可观测新息。
若,E(ut,ut)=Ik,SVAR(P)模型的滞后算子形式可以表示为:C(L)yt=ut;其中,C(L)是滞后算子L的4×4的参数矩阵。
假定结构式中误差项ut的方差-协方差矩阵为单位矩阵 I4,且 C(L)可逆,则SVAR的无穷阶的向量移动平均VMA(∞)模型可以表示如下:yt=B(L)ut;其中,B(L)是滞后算子
由 yt=A(L)εt、yt=B(L)u,可得:A(L)εt=B(L)ut
由于 A0=Ik,由此可得:A0εt= εt=B0ut或;再对其两端期望平均则可得:∑ =E(εtε't)=B0B'0,此时只要对 B0施加 k×(k-1)/2个短期约束即可识别SVAR模型。由于本文是以通货膨胀、实际经济增长、货币供给和股票价格为分析对象,构建4元4阶的SVAR(4)模型,需要施加6个短期约束即可识别。①目前国内学者多数将矩阵B的对角线各变量定义为1,然后再施加k(k-1)/2个约束,由此而产生过度识别问题。
首先,在价格粘性下,货币政策、经济增长对通货膨胀的影响存在滞后效应,当期的货币数量冲击与实际经济增长冲击对当期通胀没有影响,即a12=a13=0;股价对通胀影响需要经过一定的传导途径,如财富效应、通胀幻觉效应、托宾Q效应以及资产负债表渠道等,故当期股价冲击对通胀没有影响,即a14=0。
其次,在价格粘性下,货币政策对实际经济增长的影响是通过利率渠道发挥作用,故而可以视为货币供给冲击对当期的实际经济增长没有影响,即a23=0;股价对实际经济增长的影响则需要经过财富效应、托宾Q效应等渠道,故而可视为股票价格冲击对当期实际经济增长没有影响,即a24=0。
最后,货币政策是否应该对资产价格波动作出反应,目前理论上尚处于争议阶段,同时由“泰勒规则”可知,现实经济生活中的货币政策并没有对股价等资产价格波动作出反应,因此可视为股价冲击对当期货币政策没有影响,即a34=0。
至此,SVAR1(4)模型和SVAR2(4)模型施加短期约束后如公式(4)所示:
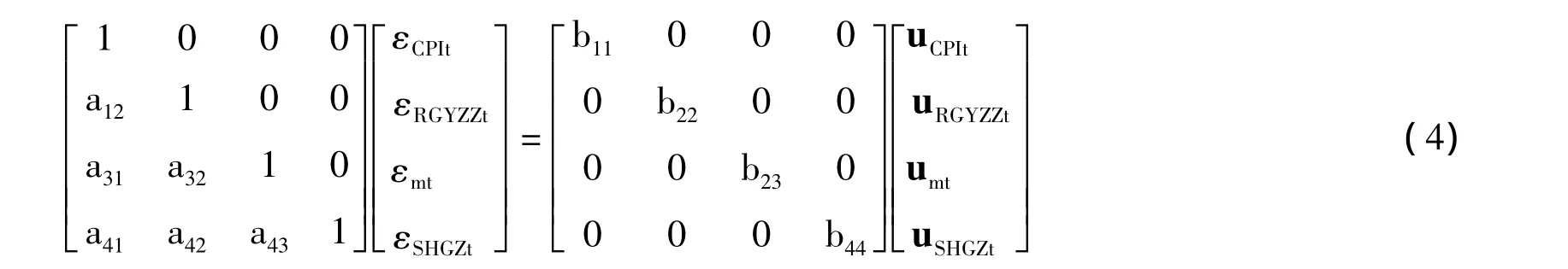
通过Eviews6.0软件,运用完全信息极大似然方法(FIML)分别对SVAR1(4)模型和SVAR2(4)模型进行未知参数估计,估计结果如表2所示:
3.基于SVAR模型的方差分解
(1)通货膨胀增幅波动的方差分解。由图2可知:第一,通胀冲击对于自身波动的贡献率呈现短期快速下降,至第16个月之后趋于稳定的特点;其中,基于SVAR1(4)模型的通胀冲击对于自身波动贡献率的最小值为13.7%,基于SVAR2(4)的通胀冲击对于自身波动贡献率的最小值为17.5%;可见,通胀冲击对其自身波动的贡献率在中长期并非很高。第二,实际工业增加值冲击对通胀波动贡献率呈现逐级攀升,至第9个月达到最大,随后渐渐趋稳;其中,基于SVAR1(4)模型的RGYZZ冲击对通胀波动贡献率的最小值在27%,基于SVAR2(4)的RGYZZ冲击对通胀波动贡献率的最小值为17.6%。第三,货币供给冲击对通胀波动的贡献率在第15个月之后趋稳,趋稳后货币供给冲击对通胀波动的贡献率在20%以上,但狭义货币m1对通胀波动的贡献率明显小于广义货币m2及实际工业增加值的冲击。第四,股价冲击对通胀波动的贡献率呈现短期快速上升,至第20个月之后逐渐趋稳的特点,趋稳后股价冲击对通胀波动的贡献率在30%以上;其中,基于SVAR1(4)模型的贡献率最大值为40%左右,基于SVAR1(4)的贡献率最大值为35%左右。由此可见,在中长期,通胀波动的主要原因来自于股价冲击和广义货币m2冲击,其次来自于实际工业增加值冲击和通胀自身冲击,由此揭示货币政策的制定应该高度关注股价波动,并作出适度响应,它将有助于物价稳定调控目标的实现。

表2 SVAR模型未知参数的估计结果

图2 通货膨胀增幅波动(CPI)的方差分解

图3 实际工业增加值增幅波动(RGYZZ)的方差分解
(2)实际工业增加值增幅波动的方差分解。由图3可知:第一,实际工业增加值波动主要来自于自身,趋稳后贡献率在60%左右;第二,实际工业增加值波动的第二个主要因素则是通胀,通胀冲击对实际工业增加值波动的贡献率趋稳后在20%左右;第三,股价冲击对实际工业增加值波动的贡献率趋稳后在10%左右以上;第四,狭义货币供给冲击对实际工业增长价值波动的贡献率较低,不到10%,广义货币供给m2冲击趋稳后在10%左右,与股价冲击的贡献率相差无几。由此可知,物价稳定有益于经济增长。
(3)货币供给增幅波动的方差分解。由图4可知:第一,货币供给波动主要是由于自身冲击造成的,其中狭义货币m1冲击对其自身波动的贡献率趋稳后约在60%,而广义货币m2在80%,说明我国广义货币的外生性与可控性比较强;第二,实际工业增长价值冲击对m1的贡献率高于对m2的贡献率;第三,股价冲击对m1波动的贡献率低于实际工业增加值,但高于通胀冲击;第四,通胀、实际工业增加值和股价等冲击对m2波动的贡献率相差不是很明显。

图4 货币供给增幅波动的方差分解

图5 上证综合指数同比增幅波动(SHGZ)的方差分解
(4)股价波动的方差分解。由图5可知:第一,股价波动主要是由于自身冲击造成的,在趋稳后其贡献率在65%;第二,货币供给冲击对股价波动的贡献率明显高于通胀冲击和实际工业增加值冲击,在趋稳后约在15%以上。第三,通胀冲击和实际工业增加值冲击对股价波动的贡献率相对较低,不到10%;但通胀冲击对股价波动的贡献率略高于实际工业增加值。由此可见,股价波动在一定程度上受制于货币政策,这在一定程度上证明了前文的理论分析。
四、结论与政策含义
在短期,由于商品价格存在价格粘性,货币数量一次性的增加,将会引致金融资产价格的短期超调失衡;但伴随着商品价格粘性逐渐消失,金融资产价格的短期超调失衡将伴随商品价格上涨而逐渐消失,市场重新达到一个新的均衡状态。从长期来看,由于货币政策“逆风向”操作规则决定了货币数量变动存在持续性的同向变动趋势。持续性的货币供给量增加或减少,使得金融资产价格的超调失衡难以在短期内得以及时纠正,使其超调效应在中长期呈现出累积叠加,由此使得金融资产价格能够在较长时间处于累积超调状态,从而使得股票价格能够在较长时间处于背离其基本面而呈现出长期的“剪刀差”现象。
从货币政策的传导过程来看,在价格粘性存在的前提下,一次性的货币供给的增减将引致利率短期超调失衡和金融资产价格短期超调失衡,并通过融资成本渠道、财富效应渠道、托宾Q效应渠道以及预期渠道作用于投资需求和消费需求,由此引发物价上涨,从而使得利率短期超调失衡和金融资产价格短期超调失衡得以纠正,市场重新达到一个新的均衡状态。同样道理,如果是连续性的同向货币数量增减冲击,将会使得金融资产价格的超调效应得以累积叠加,从而导致金融资产价格在较长期限内背离其基本面而呈现出“剪刀差”现象。如果再考虑投资者的预期中存在自我实现过程,这种预期的自我实现将导致投资者在经济向好时期对市场“好消息”会反应过度而对“坏消息”则会反应不足,促进股票价格进一步上涨,股票价格超调状态必将得到进一步加强。
由此可见,在价格粘性下,货币数量的变动并不是首先直接作用于物价水平,而是通过金融资产价格、投资需求与消费需求即国民收入的变动作用于物价水平,由此出现物价波动滞后于经济增长,而经济增长又滞后于金融资产价格。正是由于价格粘性的存在、货币数量周期性的持续性同向变动的冲击以及投资者预期的自我实现,使得金融资产价格能够在较长时间处于背离其基本面而出现“剪刀差”,并且能够先于国民经济增长、物价水平而动,先行达到其周期性顶部或底部。这意味着股票价格并不因为出现背离基本面的“剪刀差”现象而丧失经济“晴雨表”作用,反而较为提前预示宏观经济的顶部或底部的到来。如果货币当局能够将股价信息纳入货币政策规则,及时对其作出反应,则可以为前瞻性货币政策制定赢得宝贵的时间,可以有效地缩短货币政策的时滞效应,提高货币政策的有效性和前瞻性,有助于实现经济平稳增长的货币政策调控目标。
基于我国月度统计数据的协整检验表明,我国商品价格与前期商品价格、货币政策、国民收入和股票价格从长期来看存在稳定的协整关系。而基于SVAR模型的方差分解则进一步表明:(1)从中长期来看,我国通胀波动的主要动因是股价冲击和广义货币m2冲击,其次是来自于实际工业增加值冲击和通胀自身冲击;(2)除自身因素之外,通胀冲击对实际工业增加值波动的贡献率趋稳后保持在20%左右,股价冲击对实际工业增加值波动的贡献率趋稳后保持在10%左右以上;(3)股价波动主要是由于自身冲击造成的,货币供给冲击对股价波动的贡献率明显高于通胀冲击和实际工业增加值冲击,在趋稳后约在15%以上;(4)货币供给波动主要是由于自身冲击造成的,其中狭义货币冲击对其自身波动的贡献率趋稳后约在60%,而广义货币在80%。由此表明,我国货币供给尤其是广义货币m2具有很强的外生性与可控性,而货币政策对股价波动和通胀波动又具有较强的解释力,在此情况下,如果货币政策高度关注股价波动,并作出适度反应,将有助于我国的物价稳定和经济平稳增长。
[1] I Fisher.The Theory of Interest[M].New York:Macmillan,1930.
[2]M Gertler,B Bernanke.Should Central Banks Respond to Movements in Asset Prices[J].A-merican Economic Review,2001,91(2):253-257.
[3]L Kryzanowskiand,A H Rahman.Generalized Fama Proxy Hypothesis:Impact of Shocks on Phillips Curve and Relation of Stock Returns with Inflation[J].Economics Letters,2009,103(3):135-137.
[4]K Luintel,K Paudyal.Are Common Stocks a Hedge against Inflation[J].Journal of Financial Research,2006,29(1):1-19.
[5]吕江林.我国的货币政策是否应对股价变动做出反应[J].经济研究,2005,(3):80-90.
[6]孙华妤,马跃.中国货币政策与股票市场的关系[J].经济研究,2003,(7):44-53.
[7]郭田勇.资产价格、通货膨胀与中国货币政策体系的完善[J].金融研究,2006,(10):23-35.
[8]武戈.货币政策与资产价格:经典理论、美联储实践及现实思考[J].南开经济研究,2007,(4):90-105.
[9]王虎,王宇伟,范从来.股票价格具有政策指示器功能吗?——来自中国1997-2006年的经验证据[J].金融研究,2008,(6):94-108.
[10]王国松.基于价格粘性的股价超调现象的理论分析与检验[J].商业经济与管理,2010,(11):69-76.
[11]伍志文,鞠方.通货紧缩、资产膨胀与货币政策[J].管理世界,2003,(11):7-17.
[12]M Gordon.The Savings Investment and Valuation of a Corporation[J].The Review of Economics and Statistics,1962,44(1):37-51.
